
第六章自旋和角动量 复旦大学苏汝铿
第六章 自旋和角动量 复旦大学 苏汝铿
V=2 P'V V-V-ΣVtg o"o 0

第六章自旋和角动量 ·光谱线在磁场中的分裂,精细结构 ·揭示一个新的自由度:自旋 ·角动量的叠加,无耦合表象和耦合表象 自旋单态和三重态
第六章自旋和角动量 ▪ 光谱线在磁场中的分裂,精细结构 ▪ 揭示一个新的自由度:自旋 ▪ 角动量的叠加,无耦合表象和耦合表象 ▪ 自旋单态和三重态

§6.1电子自旋 >Stern-Gerlach实验 U--M=Mcos 0 a光 az cos 0
§6.1 电子自旋 ➢Stern-Gerlach实验
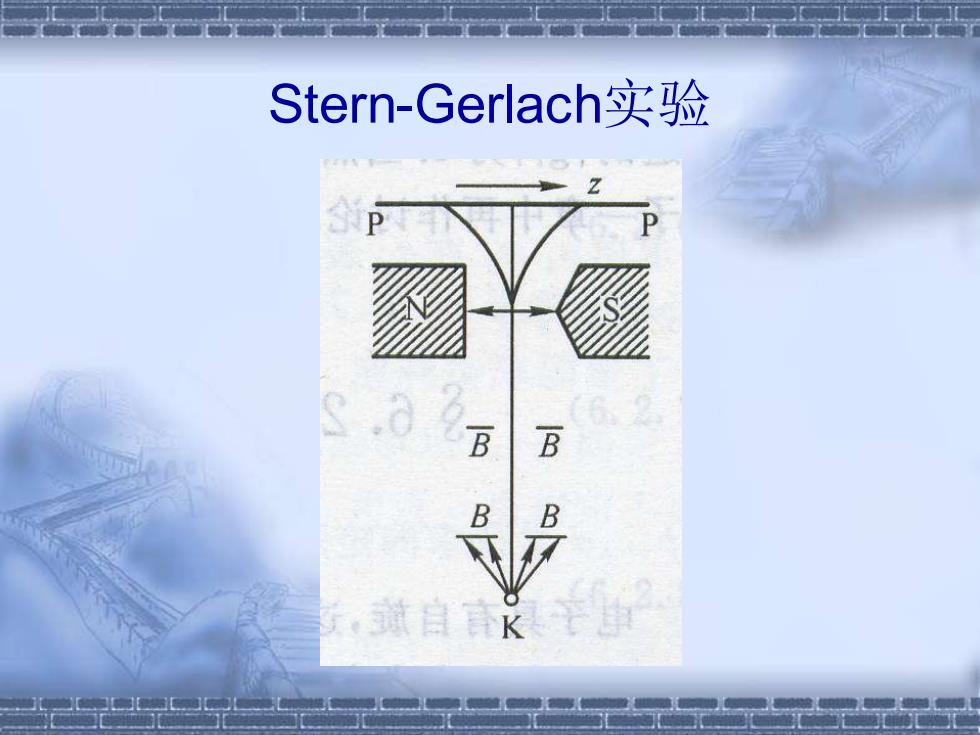
Stern-Gerlach实验 B B 关,威自K
Stern-Gerlach实验

§6.1电子自旋 >Uhlenbeck-Goudsmit理论 S.=士i/2 M,=-eS(SD或M,=±es(CGS) m mc
§6.1 电子自旋 ➢Uhlenbeck – Goudsmit 理论

§6.1电子自旋 M=土h=土M(SID或M=,ei=士MB(CGS) 2m 2mc 昌想支站业 M M S: (SD: =共e(CGS) mc M=- L(SD:M.-- eL(CGS) 2mc
§6.1 电子自旋

§6.1电子自旋 ·自旋是个内禀的物理量 ·无经典对应量 ·满足角动量对易关系
§6.1 电子自旋 • 自旋是个内禀的物理量 • 无经典对应量 • 满足角动量对易关系

§6.2电子的自旋算符和自旋函数 >电子自旋算符的矩阵表示,泡利矩阵 S×S=hS 55,-5,5,=S。 S:Sy-ihS: S.S,-S,S:=ihSy
§6.2 电子的自旋算符和自旋函数 ➢电子自旋算符的矩阵表示,泡利矩阵

§6.2电子的自旋算符和自旋函数 S2=S?=S2=h/4 游只头时拉议分面因。自面 S*-5:+5+: S=s6+1)= s=1/2
§6.2 电子的自旋算符和自旋函数