
第五章近似方法 复旦大学苏汝铿
第五章 近似方法 复旦大学 苏汝铿

Hmmm....Interesting...Now,Thog, next you go in there and see where all my other research students have gotten to..... Proto-Professor Algarth Zag,pioneer in fire research

第五章近似方法 >目的: 建立各种近似求解Schrodinger方程本征值和 本征函数的方法
第五章 近似方法 ➢目的: ▪ 建立各种近似求解Schrodinger方程本征值和 本征函数的方法
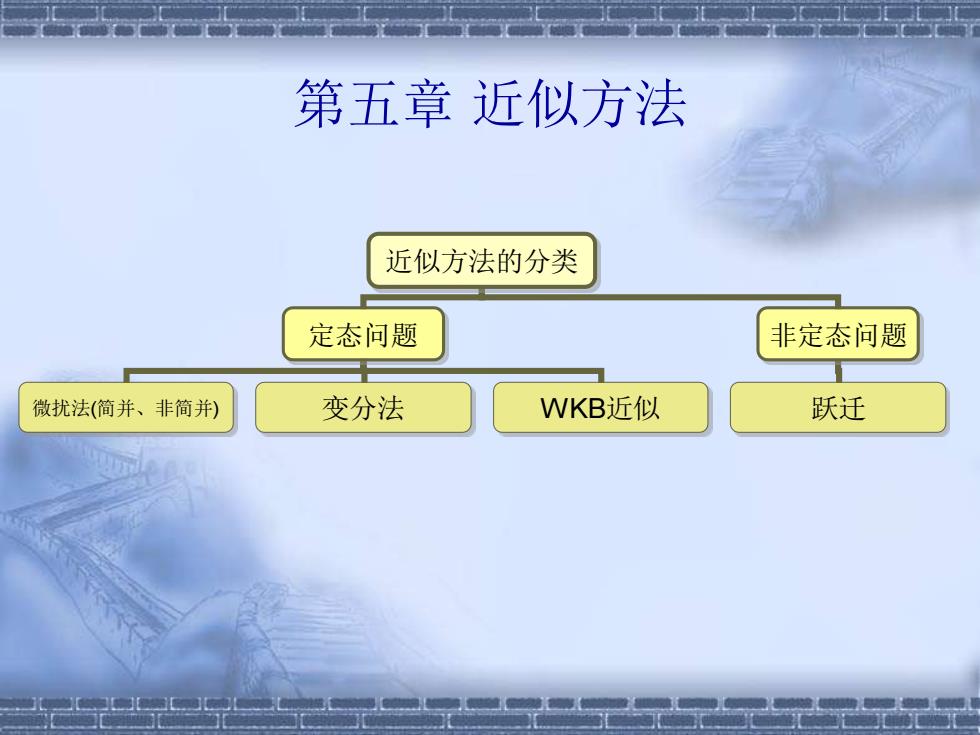
第五章近似方法 近似方法的分类 定态问题 非定态问题 微扰法(简并、非简并) 变分法 WKB近似 跃迁
第五章 近似方法 近似方法的分类 定态问题 非定态问题 微扰法(简并、非简并) 变分法 WKB近似 跃迁

§5.1非简并定态微扰论 >条件: ·H中H()定态 ·无简并,严格说来是要修正的能级无简并 H=Ho+H',H'<<Ho H的本征态及本征谱已知 分立谱(或分立谱十连续谱,但只对其中分立 谱作微扰计算)
§5.1 非简并定态微扰论 ➢条件: ▪ H中H(t)定态 ▪ 无简并,严格说来是要修正的能级无简并 ▪ H=H0+H’, H’<<H0 ▪ H0的本征态及本征谱已知 ▪ 分立谱(或分立谱+连续谱,但只对其中分立 谱作微扰计算)

§5.1非简并定态微扰论 >展开式: Hψn=(H。+入H')4n=Em中n En=E0)+E十2E%2十… 中n=0)十1十2%2十…
§5.1 非简并定态微扰论 ➢展开式:

§5.1非简并定态微扰论 (H。十λH')()+9)+λ22》+…) =(E0)+E1)十2E%2)+…)()+A妙1)+22)+…) 入”:照H必)=E0’少%0证的 入是: (H一E)=-(H-E4) 12: (H。-E)2)=-(H'-E)1+E2 09.00e 香图南尊容或,东舍不
§5.1 非简并定态微扰论

§5.1非简并定态微扰论 (H-E)∑a=-(H'-E) H'o d+E Ha='H'4dz=〈°1H'19)
§5.1 非简并定态微扰论

§5.1非简并定态微扰论 E =H'm afi)= H'm E0-E0 1=〈4.4n)=〈()+)(+)》 =〈1)+[〉+(|)]+O(入2)
§5.1 非简并定态微扰论

§5.1非简并定态微扰论 (〉+(〉=0 a+a'=0 )-=iy 0
§5.1 非简并定态微扰论