
第二章二次量子化
第二章 二次量子化

●全同多粒子体系难以用通常的波函数处理 →发展了二次量子化方法心 引入粒子占有数表象一用各单粒子态填充 的粒子数描述状态;交换对称性自动满足 十基本算符:粒子的产生算符和湮灭算符 十任意态矢和力学量均可用它们表示 十有系统的法则计算力学量的矩阵元
●全同多粒子体系引难以用通常的波函数处理 言 →发展了二次量子化方法☻ † 引入粒子占有数表象—用各单粒子态填充 的粒子数描述状态;交换对称性自动满足 † 基本算符:粒子的产生算符和湮灭算符 † 任意态矢和力学量均可用它们表示 † 有系统的法则计算力学量的矩阵元

§2.1全同粒子体系的量子态描述
§2.1 全同粒子体系的量子态描述

●为什么要引入粒子数表象? 1.全同粒子的交换对称性 何为全同粒子? 2.全同性与量子化的概念→区别于经典
●为什么要引入粒子数表象? 1. 全同粒子的交换对称性 何为全同粒子? 2. 全同性与量子化的概念→区别于经典
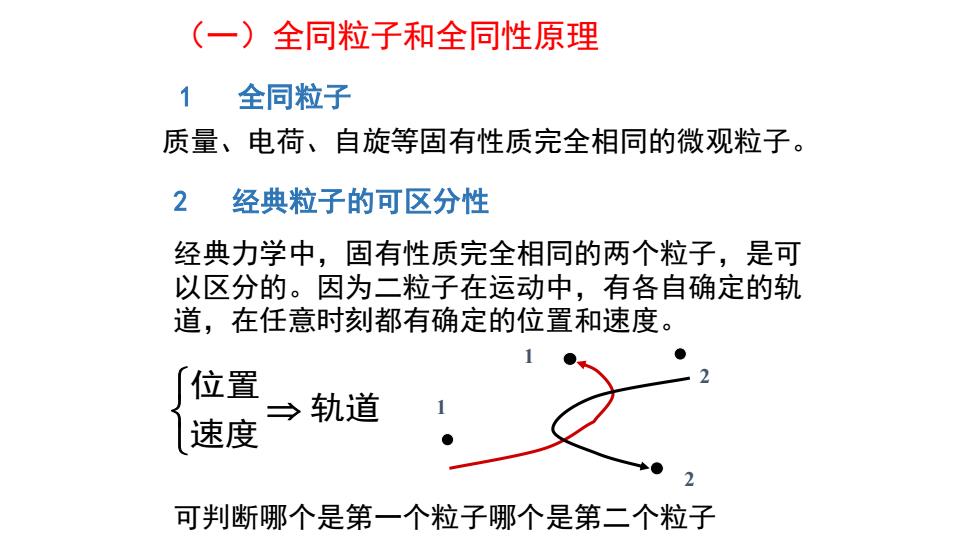
(一)全同粒子和全同性原理 1全同粒子 质量、电荷、自旋等固有性质完全相同的微观粒子。 2 经典粒子的可区分性 经典力学中,固有性质完全相同的两个粒子,是可 以区分的。因为二粒子在运动中,有各自确定的轨 道,在任意时刻都有确定的位置和速度。 1 位置 →轨道 速度 可判断哪个是第一个粒子哪个是第二个粒子
1 全同粒子 质量、电荷、自旋等固有性质完全相同的微观粒子。 2 经典粒子的可区分性 经典力学中,固有性质完全相同的两个粒子,是可 以区分的。因为二粒子在运动中,有各自确定的轨 道,在任意时刻都有确定的位置和速度。 位置 轨道 速度 可判断哪个是第一个粒子哪个是第二个粒子 1 2 1 2 (一)全同粒子和全同性原理

3微观粒子的不可区分性 服从 用 微观粒子运动 量子力学 波函数描写 在波函数重叠区粒子是 不可区分的 4全同性原理 全同粒子所组成的体系中,二全同粒子互相代 换不引起体系物理状态的改变。 全同性原理是量子力学的基本原理之一
3 微观粒子的不可区分性 微观粒子运动 服从 量子力学 用 波函数描写 在波函数重叠区粒子是 不可区分的 4 全同性原理 全同粒子所组成的体系中,二全同粒子互相代 换不引起体系物理状态的改变。 全同性原理是量子力学的基本原理之一

(二)波函数的对称性质 1 Hamilton算符的对称性 N个全同粒子组成的体系,其Hamilton量为: (g,2,…g,…4,gN,))=】 [+ug]小+空a 其中 q:={,S} 为第个粒子的坐标和自旋。 即: 调换第i和第j粒子,体系Hamilton 量不变。 户(q1,42,…q)…4,…4,)=H(41,42,…41…4…4N,t) 表明,N个全同粒子组成的体系的Hamilton量具有交换 对称性,交换任意两个粒子坐标(q,q)后不变
1 Hamilton 算符的对称性 N 个全同粒子组成的体系,其Hamilton 量为: 其 中 q r s 为 第i个粒子的坐标和自旋。 H q q q q q t U q t V q q i i i i j N i j i i N i i j N { , } ( , ) ( , ) 2 ( , , , ) ˆ 2 2 1 1 2 + = − + = 调换第 i 和第 j 粒子,体系Hamilton 量不变。 即: ( , , , ) ˆ ( , , , ) ˆ 1 2 1 2 H q q q q q t H q q q q q t j i N = i j N (二)波函数的对称性质 表明,N 个全同粒子组成的体系的Hamilton 量具有交换 对称性,交换任意两个粒子坐标(qi , qj ) 后不变

2对称和反对称波函数 考虑全同粒子体系的 含时Schrodinger方程 g,42…4…4…4w0 =i(g1,42,…4…4,…4w,t)0(4,42,…4…4…4w,) 将方程中(q,q)调换,得: ih9g9,“…94…4,0 8t =i(g1,4,…4…g:…4v,0(41,42,…4…4…4v,0 由于Hamilton量对 于(q,q)调换不 =(g1,42,…4…4…4w,t) 变 ①(41,42,…4…4…9w,t)
2 对称和反对称波函数 考虑全同粒子体系的 含时Schrodinger 方程 1 2 1 2 1 2 ( , , , ) ˆ ( , , , ) ( , , , ) i N N j i j j N i i q q q t t H q q q q q q q t q q q t q q = 将方程中(qi , qj ) 调换,得: 1 2 1 2 1 2 ( , , , ) ˆ ( , , , ) ( , , , ) j N N i j i i N j i q q q t t H q q q q q q q t q q q t q q = 由于Hamilton量对 于(qi , qj ) 调换不 变 1 2 1 2 ˆ ( , , , ) ( , , , ) N i N i j j H q q q t q q q q q t q q =

,4a…g,…9:…40 8t =i(g1,42,4…4…4w,t00(g,4…4…4:…4v,) =i(g1,42,…4:…4…4,t)(41,42,…4…4:…4N,9 表明:(q,g)调换前后的波函数都是Schrodinger方程 的解。 根据全 同性原 (41,42,…4:…4…qN,t) 描写同一状态。 理: ①(41,42,…44:…4N,t) 因此,二者相差一 常数因子
表明: (qi , qj ) 调换前后的波函数都是Schrodinger 方程 的解。 根据全 同性原 理: 1 2 1 2 ( , , , ) ( , , , ) j i i N N j q q q t q q q q q q q t 描写同一状态。 因此,二者相差一 常数因子。 1 2 1 2 1 2 ( , , , ) ˆ ( , , , ) ( , , , ) j N N i j i i N j i q q q t t H q q q q q q q t q q q t q q = 1 2 1 2 ˆ ( , , , ) ( , , , ) H q q q t q q i j N N j i = q q q q q t

④(41,42,…4j…4:…9w,)=九④(q1,42,…4…41…4N,) 再做一次(q,g)调换 Φ(41,42,…4:…4…4v,t)=2④(41,42,…4…4:…9w,t) =元2Φ(q1,42,…4:…41…9N,t) 所以 22=1 → 九=t1 对称波函数 λ=1 二粒子互换后波函数不变,即 Φ(41,42,L4,L4Lq,t)=Φ(q1,42,L9,L4:L9w,t)
1 2 1 2 ( , , , ) ( , , , ) j i N N i j = q q q t q q q t q q q q 再做一次(qi , qj ) 调换 1 2 1 2 2 1 2 ( , , , ) ( , , , ) ( , , , ) i j j N i j N N i q q q t q q q t q q q q q q q q q t = = 1 1 2 所 以 = = 1 2 1 2 1 ( , , , ) ( , , , ) i j N N j i q q q t q q q q q q q t = = L L L L L L 二粒子互换后波函数不变,即 对称波函数