
第十二章保险精算 12.1学习要求 掌握保险精算的基本任务和基本原理,懂得非寿险精算中的保险费率的厘定方法和财 务稳定性的分析方法。了解寿险精算中的趸缴纯保费、均衡纯保费、毛保费的计算方法和 责任准备金的计算方法。 12.2内容简述 12.2.1保险精算概述 1、保险精算的产生与发展 ●保险精算的产生是以哈雷慧星的发现者,英国天文学家哈雷(Ha11ey)在1693年 发表的世界上第一张生命表为标志,至今已有三百多年的历史。 ● 进入20世纪以来,保险精算学得到了长足发展,精算技术发生了根本的变化,精 算水平显著提高,精算在保险业务中具有核心作用。 保险精算是在上世纪80年未90年代初才开始了入我国的,虽然起步较晚,但在 开始引进时就与国际接轨,通过“派出去,请进来”的直接学习方式,直接吸收国 际上最新成果,直接与国外学者进行交流。目前,我国保险精算学学术水平已接近 世界先进水平。 2、保险精算的基本任务 保险精算的首要任务是保险费率的确定,其中纯费率的确定是至关重要的 ● 保险产品的定价 ● 责任准备金的计提 ● 再保险的计划安排 ● 偿付能力管理 ● 保险基金的运用 ● 保险公司财务分析及破产预警 3、保险精算的基本原理 收支相等原则:就是使保险期内纯保费收入的现金价值与支出保险金的现金价值 相等。其具体理解为: 令根据保险期间末期的保费收入的本利和(终值)及支付保险金的本利和(终 值)保持平衡来计算: ◇根据保险合同成立时的保费收入的现值和支付保险金的现值相等来计算: 根据在某一时点的保费收入和支付保险金的“本利和”或“现值”相等来计 算。 ● 大数法则:用来说明大量的随机现象由于偶然性相互抵消所呈现的必然数量规律 的一系列定理的统称。 12.2.2非寿险精算 1、保险费与保险费率的概念 保险费率(Insurance Rate)简称费率,是每一保险额单位应缴纳的保险费的比
第十二章 保险精算 12.1 学习要求 掌握保险精算的基本任务和基本原理,懂得非寿险精算中的保险费率的厘定方法和财 务稳定性的分析方法。了解寿险精算中的趸缴纯保费、均衡纯保费、毛保费的计算方法和 责任准备金的计算方法。 12.2 内容简述 12.2.1 保险精算概述 1、保险精算的产生与发展 z 保险精算的产生是以哈雷慧星的发现者,英国天文学家哈雷(Halley)在 1693 年 发表的世界上第一张生命表为标志,至今已有三百多年的历史 。 z 进入 20 世纪以来,保险精算学得到了长足发展,精算技术发生了根本的变化,精 算水平显著提高,精算在保险业务中具有核心作用。 z 保险精算是在上世纪 80 年未 90 年代初才开始了入我国的,虽然起步较晚,但在 开始引进时就与国际接轨,通过“派出去,请进来”的直接学习方式,直接吸收国 际上最新成果,直接与国外学者进行交流。目前,我国保险精算学学术水平已接近 世界先进水平。 2、保险精算的基本任务 z 保险精算的首要任务是保险费率的确定,其中纯费率的确定是至关重要的 z 保险产品的定价 z 责任准备金的计提 z 再保险的计划安排 z 偿付能力管理 z 保险基金的运用 z 保险公司财务分析及破产预警 3、保险精算的基本原理 z 收支相等原则:就是使保险期内纯保费收入的现金价值与支出保险金的现金价值 相等。其具体理解为: 根据保险期间末期的保费收入的本利和(终值)及支付保险金的本利和(终 值)保持平衡来计算; 根据保险合同成立时的保费收入的现值和支付保险金的现值相等来计算; 根据在某一时点的保费收入和支付保险金的“本利和”或“现值”相等来计 算。 z 大数法则:用来说明大量的随机现象由于偶然性相互抵消所呈现的必然数量规律 的一系列定理的统称。 12.2.2 非寿险精算 1、保险费与保险费率的概念 z 保险费率(Insurance Rate)简称费率,是每一保险额单位应缴纳的保险费的比���

率,是保险人计算保险费的标准。 ●保险费(Premium)简称保费,是投保人为转移危险,取得保险人在约定责任范围 内所承担的赔偿(或给付)责任而交付的费用。亦即:保险人为承担约定的保险赔 偿责任而向投保人收取的费用。 2、保费的构成 ·总保险费=纯保费十附加保费 纯保费Pure Premium:履行补偿或给付职能,不能有利润因素。 附加保费Loading:支付各种营业费用:包括员工的工资,企业的各种广告费用, 提供损失准备,以及企业的预期利润和应急准备金。 3、纯费率 ● 纯费率=保额损失率×(1+稳定系数) ● 保险额损失率=保险赔款总额/总保险金额×100% ·关键:稳定系数的计算。 4、附加费率 根据以往若干年度附加费用构成的实际数额和预期利润占保险金额比率确定: 附加费用总额 附加费率= X100% 保险金额总数 5、毛费率 ● 毛费率=纯费率十附加费率 由公式计算出来的毛费率,一般只是承担的某一大类标的平均数,不能适应某一 大类分项业务的风险情况需要。 ● ,保额损失率实际上是由统计资料得出的,只能是某一险种的总损失率,而且实 际业务中,根据不同风险要按具体情况分类制定。 ● ,在以往年度统计求得的保额损失率基础上,针对不同标的,风险性质和风险程 度,分项调整,这种调整即级差费率。 12.2.3寿险精算 1、生命表:是指在一定的调查时期和一定国家或地区,根据一定的人群类别(如男性.女 性)等实际而完整的统计资料,经过分析、整理、计算出某一人群中各种年龄的人的生存 和死亡概率,汇编而成的一种表格。 2、生命表内容 按年龄死亡率编制,反映一批人(最少十万/一百万人为单位)从出生后陆续死亡的 全过程。即从0岁起,逐年计算每个年龄人的生存人数,死亡人数,直至表上人全死为止。 生命表中规定最高年龄0。生命表中次目有: ●x:当年生存者的年龄。 ● I:生存数,指从初始年龄至满x岁尚生存的人数。 ● d:x岁的人一年内死亡人数,即I,中,从x→x+1岁一年中死亡人数 d=1-1 p:生存率,x→x+1岁仍生存的概率P.=1+1/1
率,是保险人计算保险费的标准。 z 保险费(Premium)简称保费,是投保人为转移危险,取得保险人在约定责任范围 内所承担的赔偿(或给付)责任而交付的费用。亦即:保险人为承担约定的保险赔 偿责任而向投保人收取的费用。 2、保费的构成 z 总保险费=纯保费+附加保费 z 纯保费 Pure Premium:履行补偿或给付职能,不能有利润因素。 z 附加保费 Loading:支付各种营业费用:包括员工的工资,企业的各种广告费用, 提供损失准备,以及企业的预期利润和应急准备金。 3、纯费率 z 纯费率=保额损失率×(1+稳定系数) z 保险额损失率=保险赔款总额/总保险金额 ×100% z 关键:稳定系数的计算。 4、附加费率 根据以往若干年度附加费用构成的实际数额和预期利润占保险金额比率确定: 附加费用总额 附加费率 = ╳ 100% 保险金额总数 5、毛费率 z 毛费率 = 纯费率 + 附加费率 z 由公式计算出来的毛费率,一般只是承担的某一大类标的平均数,不能适应某一 大类分项业务的风险情况需要。 z ∵保额损失率实际上是由统计资料得出的,只能是某一险种的总损失率,而且实 际业务中,根据不同风险要按具体情况分类制定。 z ∴在以往年度统计求得的保额损失率基础上,针对不同标的,风险性质和风险程 度,分项调整,这种调整即级差费率。 12.2.3 寿险精算 1、生命表:是指在一定的调查时期和一定国家或地区,根据一定的人群类别(如男性.女 性)等实际而完整的统计资料,经过分析、整理、计算出某一人群中各种年龄的人的生存 和死亡概率,汇编而成的一种表格。 2、生命表内容 按年龄死亡率编制,反映一批人(最少十万/一百万人为单位)从出生后陆续死亡的 全过程。即从 0 岁起,逐年计算每个年龄人的生存人数,死亡人数,直至表上人全死为止。 生命表中规定最高年龄ω 。生命表中次目有: z x :当年生存者的年龄。 z xl :生存数,指从初始年龄至满 x 岁尚生存的人数。 z x d : x 岁的人一年内死亡人数,即 xl 中,从 x → x +1 岁一年中死亡人数 x x x 1 d ll = − + z x p :生存率, x → x +1岁仍生存的概率 x x x 1 p l l = +

● q.:死亡率,x→x+1岁前死亡的概率q=d/1 ● e:平均余命或生命期望值,表示x岁的人以后还能生存的平均年数。 ● 折现率为i,则v=1/(1+i) 3、定期人寿保险的纯保费 假设保险期限为年。按照定期人寿保险的承保条件,如果被保险人在保险期内遭遇 死亡,则由保险公司按保险金额给付:如果被保险人生存至期满,则保险公司无须支付。 假定被保险人的年龄为x岁,年初每个投保人应缴的纯保费为A元: L,A dx dm dx*-1 012 x-1xx+1x+2 x+2-1x+2 14=ldv+ld++ld 4n=dy+d++d-心 Ai=dvtdvtd n-ar"+d++d) 4、纯粹生存保险的纯保险费E 纯粹生存保险提供被保险人在某一年龄之后的生活收入。 生存保险以被保险人在一定时期内继续生存为条件,由保险人给付保险金的责任。 ● 假若被保险人不幸在期内死亡,则合同终止,保险人不作任何给付。 生存保险金给付的多少,由到期时尚生存的被保险人数量决定。 D.=V*1 InEx=v"Ixtn →E,=4 1..v* →nE= D D
z x q :死亡率, x → x +1岁前死亡的概率 x x x q dl = z x e :平均余命或生命期望值,表示 x 岁的人以后还能生存的平均年数。 z 折现率为i ,则ν = + 1 (1 )i 3、定期人寿保险的纯保费 假设保险期限为 n 年。按照定期人寿保险的承保条件,如果被保险人在保险期内遭遇 死亡,则由保险公司按保险金额给付;如果被保险人生存至期满,则保险公司无须支付。 假定被保险人的年龄为 x 岁,年初每个投保人应缴的纯保费为 1 Ax:n 元: ( ) 1 2 :1 1 2 1 1 1 : 2 1 1 1 : 1 2 1 1 1 : 11 1 n x xn x x x n n x x xn x n x n x x xn x n x x x nx x x xn x n x x lA dv d v d v dv d v d v A l dv d v d v A l dv d v d v A l v + +− + +− + +− ++ + + +− = + ++ + ++ = + ++ = + ++ = " " " " 4、纯粹生存保险的纯保险费 n x E z 纯粹生存保险提供被保险人在某一年龄之后的生活收入。 z 生存保险以被保险人在一定时期内继续生存为条件,由保险人给付保险金的责任。 假若被保险人不幸在期内死亡,则合同终止,保险人不作任何给付。 z 生存保险金给付的多少,由到期时尚生存的被保险人数量决定。 . x Dx x =ν l . . . . . n xn x xn n x n n x x n x x n n x x x x n n x x l E vl v l E l vl v E l v D E D + + + + = ⇒ = ⇒ = ⇒ =

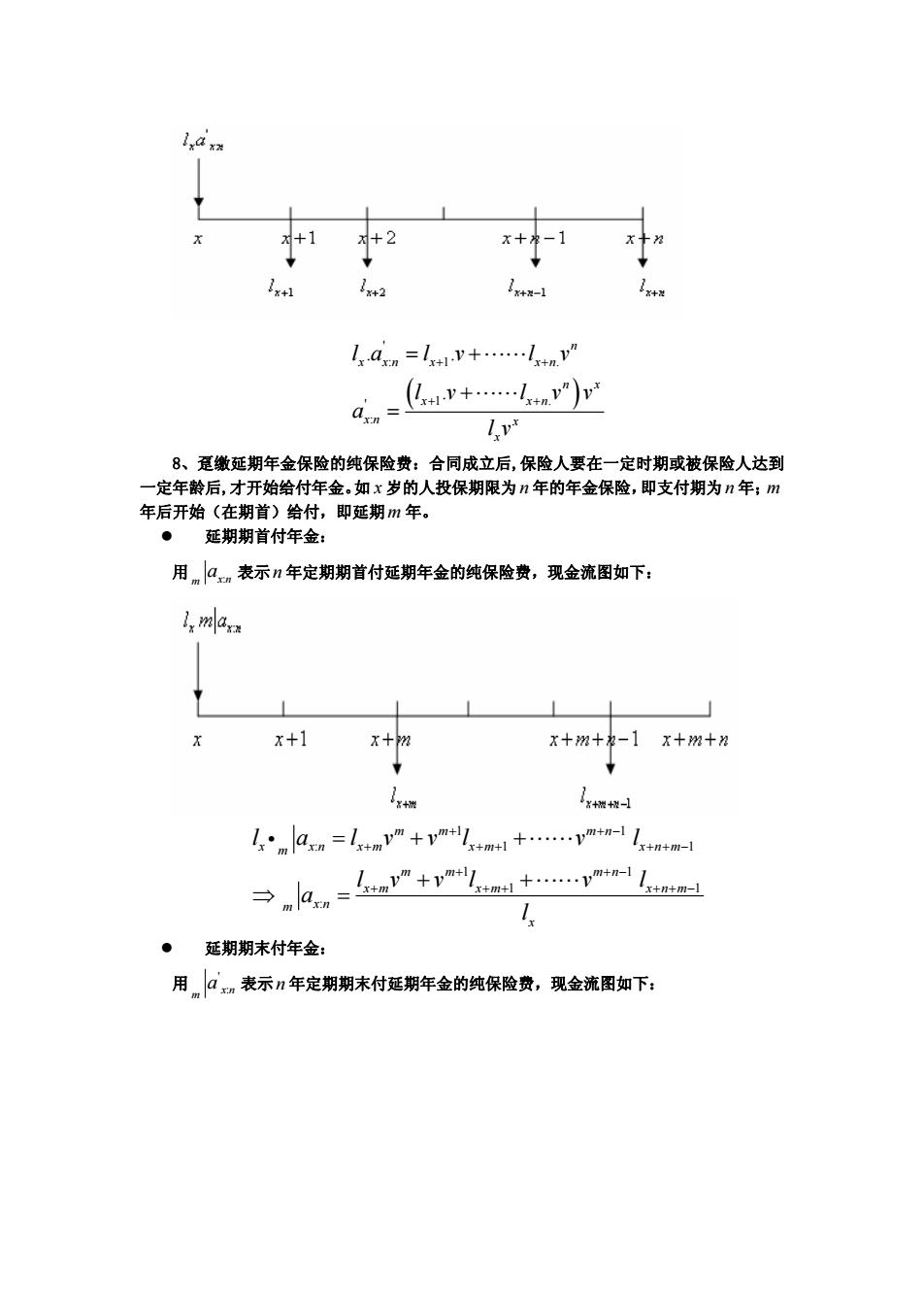
5、混合保险的纯保险费 ●混合保险是一种生死合险,即被保险人不论生存或死亡,到达一定时期后,保险 人均须给付定额保险金。 混合保险可看作定期保险与生存保险的组合。 Aon =nEs+Acn Dxtn+M:-Msn D 6、年金保险 ● 一种承诺在一定时期给付一定款项的保险。 ● 保险公司对年金保险的承保责任是被保险人的终身或者在一定时期内,被保险人 生存时每隔一定时期(一般为一年),由保险公司按期支付一次年金直至被保险人死 亡或保险期限届满为止。 7、趸缴即期年金保险的纯保险费:收到保费后,即开始支付年金。 ●期首付年金: ◇假定x岁的人投保为n年的年金保险。 令保险公司每年初支付的保险金分别为元、11元、…、+m-1元。 ¢投保人应缴的纯保费为axm。 1axn 为+1 x+2 X十 x十2 x x*1 x+-】 1an=l+lx41v+…+1xn-1v- an=4+++n D+D1+…Dxt-l →an= D ●期末付年金: ◇假定x岁的人投保为n年的年金保险。 令保险公司每年初支付的保险金分别为1+1元、12元、…、I+n元。 ☆投保人应缴的纯保费为an·
5、混合保险的纯保险费 z 混合保险是一种生死合险,即被保险人不论生存或死亡,到达一定时期后,保险 人均须给付定额保险金。 z 混合保险可看作定期保险与生存保险的组合。 1 xn n x xn : : x n x xn x A EA D MM D + + = + + − = 6、年金保险 z 一种承诺在一定时期给付一定款项的保险。 z 保险公司对年金保险的承保责任是被保险人的终身或者在一定时期内,被保险人 生存时每隔一定时期(一般为一年),由保险公司按期支付一次年金直至被保险人死 亡或保险期限届满为止。 7、趸缴即期年金保险的纯保险费:收到保费后,即开始支付年金。 z 期首付年金: 假定 x 岁的人投保为n 年的年金保险。 保险公司每年初支付的保险金分别为 xl 元、 x 1 l + 元、"、 x n 1 l + − 元。 投保人应缴的纯保费为 x:n a 。 1 :1 1 1 1 1 : 1 1 : .. . . . n x xn x x x n n x x xn x n x x x Xn x n x la l l v l v llv l v a l DD D a D − + +− − + +− + +− =+ + + +++ = + + ⇒ = "" "" "" z 期末付年金: 假定 x 岁的人投保为n 年的年金保险。 保险公司每年初支付的保险金分别为 x 1 l + 元、 x 2 l + 元、"、 x n l + 元。 投保人应缴的纯保费为 ' x:n a 。 ������
+2 是x*2 axn=1x+1v+…lxtn” x+1v+…lx+nv四y Ly* 8、趸缴延期年金保险的纯保险费:合同成立后,保险人要在一定时期或被保险人达到 一定年龄后,才开始给付年金。如x岁的人投保期限为n年的年金保险,即支付期为n年;m 年后开始(在期首)给付,即延期m年。 ·延期期首付年金: 用man表示n年定期期首付延期年金的纯保险费,现金流图如下: 1,mam X x+1 x+ x+物+为-1x十州+2 x+根+w-】 mlan=l+nm+vm+l+m1t…vn- x+n+m-1 【x+n+m-] 延期期末付年金: 用,口n表示n年定期期末付延期年金的纯保险费,现金流图如下:
( ) ' :1 . 1 . ' : . . . n x xn x x n n x x xn x n x x la l v l v l v l vv a l v + + + + = + + = "" "" 8、趸缴延期年金保险的纯保险费:合同成立后,保险人要在一定时期或被保险人达到 一定年龄后,才开始给付年金。如 x 岁的人投保期限为 n 年的年金保险,即支付期为 n 年;m 年后开始(在期首)给付,即延期 m 年。 z 延期期首付年金: 用 m x:n a 表示n 年定期期首付延期年金的纯保险费,现金流图如下: 1 1 : 11 1 1 1 1 : m m mn x xn x m x m x n m m m m mn xm xm xnm m x n x l a lv vl v l lv vl v l a l + +− + + + ++ − + +− + + + ++ − =+ + + + ⇒ = i "" "" z 延期期末付年金: 用 ' x:n m a 表示 n 年定期期末付延期年金的纯保险费,现金流图如下:
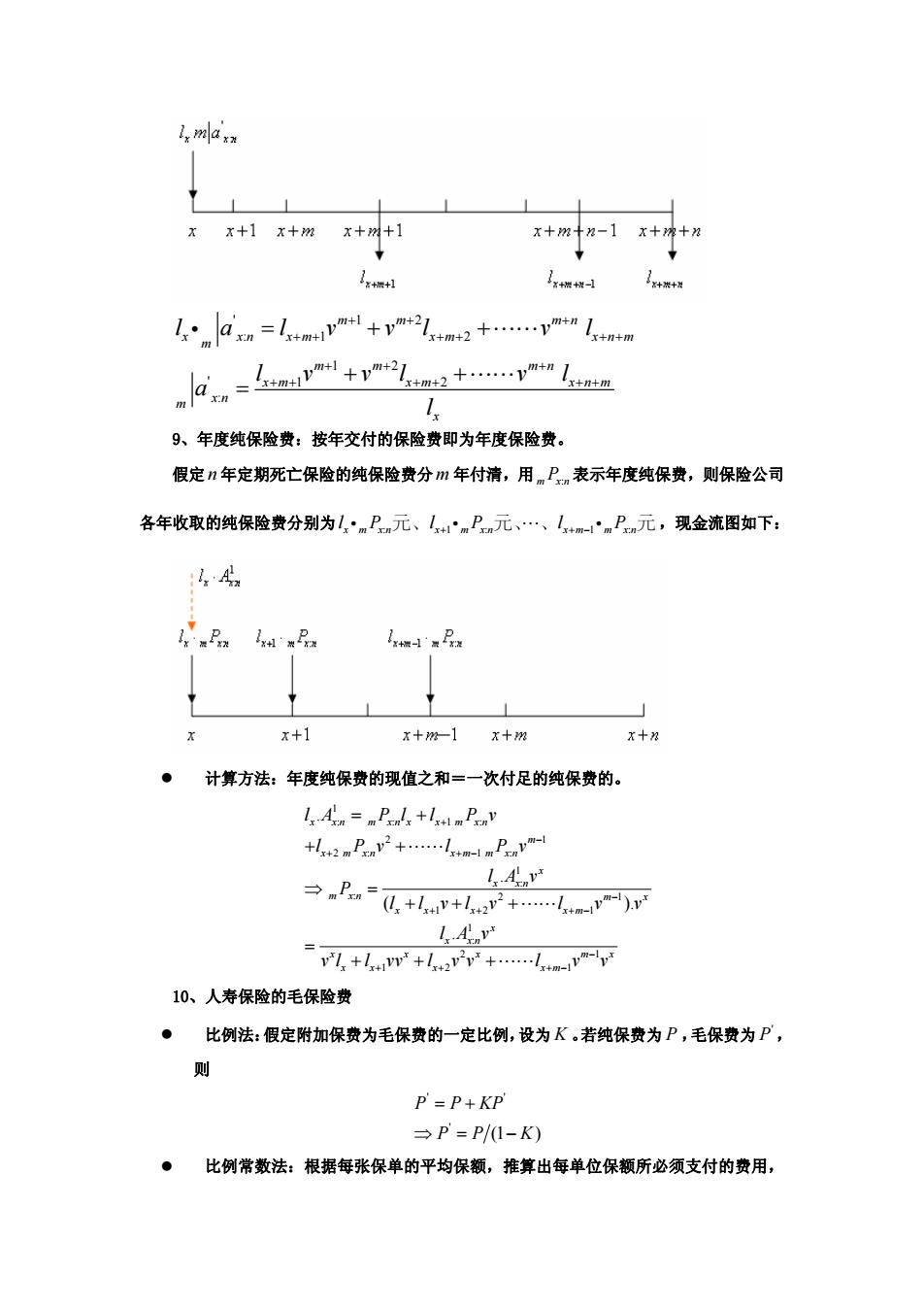
lmax xx+1 x+m x+十2-1 x++1 g+根+w-】 man=ltm4m1+vmt2x+mt2+…ym+n x+n+m a 9、年度纯保险费:按年交付的保险费即为年度保险费。 假定年定期死亡保险的纯保险费分m年付清,用,P表示年度纯保费,则保险公司 各年收取的纯保险费分别为mPn元、I1‘mPn元、…、Ix+m-'mPn元,现金流图如下: xHwR 1w1 x+1 x+m-1x+% x+2 计算方法:年度纯保费的现值之和=一次付足的纯保费的。 l An=mPds +lsemPy +2mPn2+…lm-1mnym lAny .P.0,+l+l2r+n lAny v+lw+l22p+…xmym-v 10、人寿保险的毛保险费 。比例法:假定附加保费为毛保费的一定比例,设为K。若纯保费为P,毛保费为P, 则 P=P+KP →P=P/1-K) ● 比例常数法:根据每张保单的平均保额,推算出每单位保额所必须支付的费用
' 12 :1 2 1 2 ' 1 2 : m m mn x xn x m x m x n m m m m mn xm xm xnm x n m x l a l v vl v l l v vl v l a l ++ + + + + + ++ ++ + + + + + ++ =+ + + + = i "" "" 9、年度纯保险费:按年交付的保险费即为年度保险费。 假定 n 年定期死亡保险的纯保险费分 m 年付清,用 m xn P: 表示年度纯保费,则保险公司 各年收取的纯保险费分别为 x m xn x m xn x m m xn : 1: 1: lP l P l P + +− i i "i 元、 元、 、 元,现金流图如下: z 计算方法:年度纯保费的现值之和=一次付足的纯保费的。 1 : : 1: 2 1 2: 1: 1 : : 2 1 12 1 1 : 2 1 12 1 . . ( ). . x xn m xn x x m xn m x m xn x m m xn x x xn m xn m x x x x xm x x xn x x x mx x x x xm lA Pl l Pv l Pv l Pv lAv P l lvl v l v v lAv v l l vv l v v l v v + − + +− − + + +− − + + +− = + + + ⇒ = ++ + = ++ + "" "" "" 10、人寿保险的毛保险费 z 比例法:假定附加保费为毛保费的一定比例,设为 K 。若纯保费为 P ,毛保费为 ' P , 则 ' ' ' (1 ) P P KP PP K = + ⇒= − z 比例常数法:根据每张保单的平均保额,推算出每单位保额所必须支付的费用

作为一个固定常数(用C表示),然后再确定一个毛保费的比例作为附加费用,则 P=P+KP+C =P=(P+C)/1-K) 11、责任准备金及其计算 ●基本原理:1年以前全部已收纯保险费的积存值十【年以后全部未收纯保险费的现 值=根据生命表1年以前已付保险金的积存值十【年以后保险责任的现值 ●责任准备金的计算方法: 责任准备金=1年以前全部已收纯保险费的积存值一根据生命表[年以前已付保险金的积存 值(过去法) 或 责任准备金=【年以后保险责任的现值一【年以后全部未收纯保险费的现值(未来法) 12.3本章知识点 保险精算的基本原理,非寿险精算中的保险费的厘定方法和大数的测定,寿险精算中 的趸缴纯保费,均衡纯保费、毛保费的计算和理论责任准备金、实际责任准备金的计算。 12.4思考题 1、寿险精算和非寿险精算的基本任务有哪些? 2、大数的测定有何作用? 12.5例题与习题 1、某35岁人投保三年期的定期死亡保险,保险金额为10000元,①若此人保费采取 趸缴的形式,请计算此人应缴纳的趸缴净保费;②若此人保费采取年交付的形式,请计算 年交纯保费。(1s=966400,16=965123,17=963737 ds=1277,d6=1386,d,=1508,预定利率i=2.5%) ①若此人保费采取趸缴的形式 lsA53=ds(1+i)+d6(1+i)2+d,(1+i)- 4s=s1+'+dx0+02+d,+ 4=1277x1+0.025'+1386x1+0.025)+1508×0+0.025) 966400 A53=0.004103(元) 则此人应缴纳的趸缴净保费=10000×A53=10000×0.004103=41.03(元) ②若此人保费采取年交付的形式 第1种方法:
作为一个固定常数(用C 表示),然后再确定一个毛保费的比例作为附加费用,则 ' ' ' ( ) (1 ) P P KP C P PC K =+ + ⇒=+ − 11、责任准备金及其计算 z 基本原理:t 年以前全部已收纯保险费的积存值+t 年以后全部未收纯保险费的现 值=根据生命表t 年以前已付保险金的积存值+t 年以后保险责任的现值 z 责任准备金的计算方法: 责任准备金=t 年以前全部已收纯保险费的积存值-根据生命表t 年以前已付保险金的积存 值 (过去法) 或 责任准备金=t 年以后保险责任的现值-t 年以后全部未收纯保险费的现值 (未来法) 12.3 本章知识点 保险精算的基本原理,非寿险精算中的保险费的厘定方法和大数的测定,寿险精算中 的趸缴纯保费,均衡纯保费、毛保费的计算和理论责任准备金、实际责任准备金的计算。 12.4 思考题 1、 寿险精算和非寿险精算的基本任务有哪些? 2、 大数的测定有何作用? 12.5 例题与习题 1、某 35 岁人投保三年期的定期死亡保险,保险金额为 10000 元,① 若此人保费采取 趸缴的形式,请计算此人应缴纳的趸缴净保费;② 若此人保费采取年交付的形式,请计算 年交纯保费。( 35 36 37 lll === 966400, 965123, 963737, 35 36 37 ddd === 1277, 1386, 1508, 预定利率i = 2.5% ) ① 若此人保费采取趸缴的形式 1 123 35 35:3 35 36 37 123 1 35 36 37 35:3 35 123 1 35:3 1 35:3 (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) 1277 (1 0.025) 1386 (1 0.025) 1508 (1 0.025) 966400 0.004103 lA d i d i d i d id id i A l A A −−− −−− −−− = ++ ++ + ++ ++ + = ×+ + ×+ + ×+ = = (元) 则此人应缴纳的趸缴净保费= 1 35:3 10000 10000 0.004103 41.03 ×= × = A (元) ② 若此人保费采取年交付的形式 第 1 种方法:

4sAs=15‘353+16‘3P5g(1+i)+1,‘33(1+i) 135A353 Bs+1+0+,0+ 966400×0.004103 3B-966400+965123x0+0.025)+963737x1+0.025)7 =0.001403(元) 则此人应缴纳的年交纯保费=10000×,P53=10000×0.001403=14.03(元) 第2种方法: 153s3+6‘33(1+i)+1,‘3P531+)2=ds(1+i)+d6(1+)2+d,1+i)3 3Bg=ds1+'+4s0+02+d60+i少 5+16(1+i)+13,(1+i)2 1277×(1+0.025)+1386×(1+0.025)2+1508×(1+0.025)- 333= 966400+965123×(1+0.025)1+963737×(1+0.025)2 3P53=0.001403(元) 则此人应缴纳的年交纯保费=10000×3P3=10000×0.001403=14.03(元) 2、某35岁人投保二年期的定期死亡保险,保险金额为10000元,①若此人保费采 取趸缴的形式,请计算此人应缴纳的趸缴净保费;②若此人保费采取年交付的形式,请计 算年交纯保费。(15=966400,16=965123,17=963737, d5=1277,d6=1386,d,=1508,预定利率i=2.5%) ①若此人保费采取趸缴的形式 15A52=d4s(1+i)+d6(1+i)2 42=4sl+)+ds1+02 135 42=1277×0+0.025+1386×1+0.025) 966400 A452=0.002654(元) 则此人应缴纳的趸缴净保费=10000×A2=10000×0.002654=26.54(元) ②若此人保费采取年交付的形式 第1种方法:
1 12 35 35:3 35 3 35:3 36 3 35:3 37 3 35:3 1 35 35:3 3 35:3 1 2 35 36 37 3 35:3 1 2 (1 ) (1 ) (1 ) (1 ) 966400 0.004103 966400 965123 (1 0.025) 963737 (1 0.025) 0.001403 lA l P l P i l P i l A P ll i l i P − − − − − − = ⋅ + ⋅ ⋅+ + ⋅ ⋅+ = + ⋅+ + ⋅+ × = + ×+ + ×+ = (元) 则此人应缴纳的年交纯保费= 3 35:3 10000 10000 0.001403 14.03 × P =× = (元) 第 2 种方法: 1 2 123 35 3 35:3 36 3 35:3 37 3 35:3 35 36 37 123 35 36 36 3 35:3 1 2 35 36 37 1 2 3 35:3 (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) 1277 (1 0.025) 1386 (1 0.025) 1508 (1 0.02 lPlP i lP i d i d i d i d id id i P ll i l i P − − −−− −−− − − − − ⋅ + ⋅ ⋅+ + ⋅ ⋅+ = + + + + + ++ ++ + = + ⋅+ + ⋅+ ×+ + ×+ + ×+ = 3 1 2 3 35:3 5) 966400 965123 (1 0.025) 963737 (1 0.025) P 0.001403 − − − + ×+ + ×+ = (元) 则此人应缴纳的年交纯保费= 3 35:3 10000 10000 0.001403 14.03 × P =× = (元) 2、某 35 岁人投保二年期的定期死亡保险,保险金额为 10000 元, ① 若此人保费采 取趸缴的形式,请计算此人应缴纳的趸缴净保费;② 若此人保费采取年交付的形式,请计 算年交纯保费。( 35 36 37 lll === 966400, 965123, 963737, 35 36 37 ddd === 1277, 1386, 1508, 预定利率i = 2.5% ) ① 若此人保费采取趸缴的形式 1 12 35 35:2 35 36 1 2 1 35 36 35:2 35 1 2 1 35:2 1 35:2 (1 ) (1 ) (1 ) (1 ) 1277 (1 0.025) 1386 (1 0.025) 966400 0.002654 lA d i d i d id i A l A A − − − − − − = ++ + ++ + = ×+ + ×+ = = (元) 则此人应缴纳的趸缴净保费= 1 35:2 10000 10000 0.002654 26.54 ×= × = A (元) ② 若此人保费采取年交付的形式 第 1 种方法:

13s452=ls‘2P52+l6‘252(1+i)1 135452 2216+1s1+i 966400×0.002654 ,5:-966400+965123x0+0025T-00134元) 则此人应缴纳的年交纯保费=10000×2P52=10000×0.001344=13.44(元) 第2种方法: 1s‘2P2+l6“2P52(1+i)=ds(1+i0+d6(1+i)2 22=4s1+0+ds1+ 1s+l6(1+i)1 1277×(1+0.025)+1386×(1+0.025)-2 2P352= 966400+965123×(1+0.025)- 2P2=0.001354(元) 则此人应缴纳的年交纯保费=10000×2P52=10000×0.001354=13.54(元)
1 1 35 35:2 35 2 35:2 36 2 35:2 1 35 35:2 2 35:2 1 35 36 2 35:2 1 (1 ) (1 ) 966400 0.002654 0.001344 966400 965123 (1 0.025) lA l P l P i l A P ll i P − − − = ⋅ + ⋅ ⋅+ = + ⋅+ × = = + ×+ (元) 则此人应缴纳的年交纯保费= 2 35:2 10000 10000 0.001344 13.44 × P =× = (元) 第 2 种方法: 1 12 35 2 35:2 36 2 35:2 35 36 1 2 35 36 2 35:2 1 35 36 1 2 2 35:2 1 2 35:2 (1 ) (1 ) (1 ) (1 ) (1 ) (1 ) 1277 (1 0.025) 1386 (1 0.025) 966400 965123 (1 0.025) 0.001354 lPlP i d i d i d id i P ll i P P − − − − − − − − − ⋅ + ⋅ ⋅+ = + + + ++ + = + ⋅+ ×+ + ×+ = + ×+ = (元) 则此人应缴纳的年交纯保费= 2 35:2 10000 10000 0.001354 13.54 × P =× = (元)