
排列组合 1.两个基本原理 分类加法计数原理 分步乘法计数原理
1. 两个基本原理 分类加法计数原理 分步乘法计数原理 排列组合
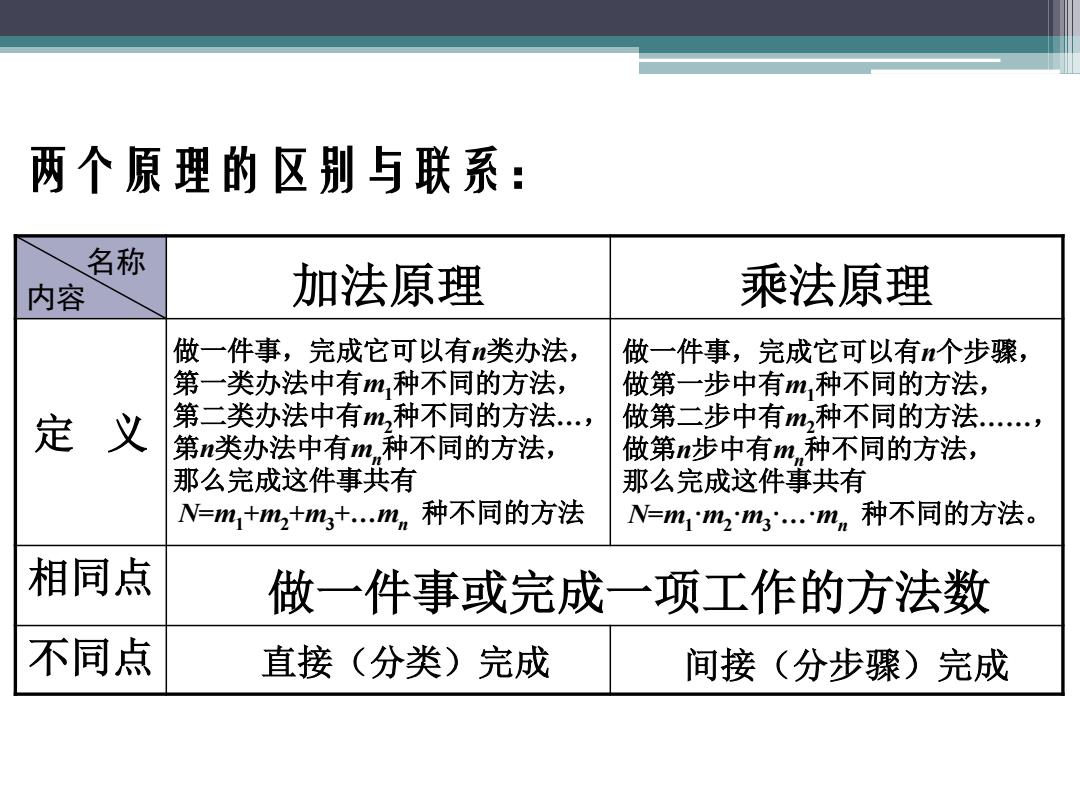
两个原理的区别与联系: 名称 内容 加法原理 乘法原理 做一件事,完成它可以有n类办法, 做一件事,完成它可以有个步骤, 第一类办法中有m种不同的方法, 做第一步中有m,种不同的方法, 定 义 第二类办法中有m,种不同的方法.., 做第二步中有m,种不同的方法., 第n类办法中有m,种不同的方法, 做第n步中有m,种不同的方法, 那么完成这件事共有 那么完成这件事共有 N=m1+m2+m+..mn种不同的方法 N=m1m2%3.mn种不同的方法。 相同点 做一件事或完成一项工作的方法数 不同点 直接(分类)完成 间接(分步骤)完成
名称 内容 加法原理 乘法原理 定 义 相同点 不同点 做一件事,完成它可以有n个步骤, 做第一步中有m1种不同的方法, 做第二步中有m2种不同的方法……, 做第n步中有mn种不同的方法, 那么完成这件事共有 N=m1·m2·m3·…·mn 种不同的方法。 两个原理的区别与联系: 做一件事或完成一项工作的方法数 直接(分类)完成 间接(分步骤)完成 做一件事,完成它可以有n类办法, 第一类办法中有m1种不同的方法, 第二类办法中有m2种不同的方法…, 第n类办法中有mn种不同的方法, 那么完成这件事共有 N=m1+m2+m3+…mn 种不同的方法

例1某校组织学生分4个组从3 处风景点中选一处去春游,则不 同的春游方案的种数是 A.C B.P C.34 D.4 (选C)
例1 某校组织学生分4个组从3 处风景点中选一处去春游,则不 同的春游方案的种数是 A. B. C. D. C3 4 P3 4 4 3 3 4 ( 选 C)

例2 有不同的数学书7本,语文书 5本,英语书4本,由其中取出不是 同一学科的书2本,共有多少种不 同的取法? (7X5+7×4+5X4=83)
例2 有不同的数学书7本,语文书 5本,英语书4本,由其中取出不是 同一学科的书2本,共有多少种不 同的取法? (7×5 + 7×4 + 5×4 = 83)

例3 将数字1、2、3、4填入标号为1、 2、3、4的四个方格里,每格填一个数 字,则每个方格的标号与所填的数字都 不相同的填法共有 A.6种 B.9种 C.11种 D.23种 (3X3X1=9)
例3 将数字1、2、3、4 填入标号为1、 2、3、4 的四个方格里 , 每格填一个数 字,则每个方格的标号与所填的数字都 不相同的填法共有 A. 6 种 B. 9种 C.11种 D.23种 ( 3×3×1= 9)

2.排列、组合的意义 把握排列和组合的区别与联系, 抓住“顺序”这个关键
2. 排列、组合的意义 把握排列和组合的区别与联系, 抓住“顺序”这个关键

3.排列数、组合数计算公式 P0=n(n-1)-(n-2…(n-m+1) Pm=n(n-1)(n-2)…3:21 n! (规定0!=1) (n-m)!
( 1) ( 2) 3 2 1 ( 1) ( 2) ( 1) = ⋅ − ⋅ − ⋅ ⋅ = ⋅ − ⋅ − − + n n n n n n n m P P n n m n ( )! ! n m n Pm n − = (规定 0!=1) 3. 排列数、组合数计算公式

从n个不同元素中取出m个元素的 排列数 Pm=C·P Un 二 D m n(n-1)(n-2)..(n-m+1) 二 m! n! 二 (C9=1) m!(n-m)!
从 n 个不同元素中取出m个元素的 排列数 m m m n m Pn = C ⋅ P ( 1) !( )! ! ! ( 1)( 2)...( 1) 0 = − = − − − + = = n m m m m n n C m n m n m n n n n m P P C

4.组合数的两个性质 C=C CH=CC
4. 组合数的两个性质 1 1 − + − = + = m n m n m n n m n m n C C C C C

例4学生要从六门课中选学两门: (1)有两门课时间冲突,不能同时 学,有几种选法? (2)有两门特别的课,至少选学其 中的一门,有几种选法?
例 4 学生要从六门课中选学两门: (1)有两门课时间冲突,不能同时 学,有几种选法? (2)有两门特别的课,至少选学其 中的一门,有几种选法?