
序言 。什么是“代数”? 用字母代替数一便于研究量之间的规律。 ·《线性代数》研究的内容 用字母代替数组、代替数组的组, 研究数组的运算、关系及其应用的一门学科。 例如 a11X1+412X2=b, 1= 1 412 b 021X1+022X2=b2 a21 21 4=(a1a2b) a11 =(a1a2b2) B.=
什么是“代数” ? 用字母代替数 —— 便于研究量之间的规律。 《线性代数》研究的内容 + = + = . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 用字母代替数组、 11 12 1 1 2 21 22 2 a ab a ab ββ β = = = ( ) ( ) 1 11 12 1 2 21 22 2 aab aab α α = = 研究数组的运算、关系及其应用的一门学科。 代替数组的组 , 11 12 1 21 21 2 aab A aab = 例如 序 言

第一章彳 行列式 本章主要内容: n阶行列式定义(§1.1)、 性质(§1.2、§1.3); 克莱姆法则: n元线性方程组与n阶行列式的关系(§1.4)
第一章 行列式 本章主要内容: n阶行列式 定义(§1.1)、 性质(§1.2、§1.3); 克莱姆法则: n元线性方程组与n阶行列式的关系(§1.4)
§1.1n阶行列式 一、二阶、三阶行列式 1.二阶行列式 分析二元线性方程组的解 411七1+412X2=b1, 021X1+422X2=b2: 对角线法则:主对角线上 两元素乘积减去副对角线 上两元素乘积 则当D≠0,x= X2 【注】分母都为原方 D 程组的系数行列式
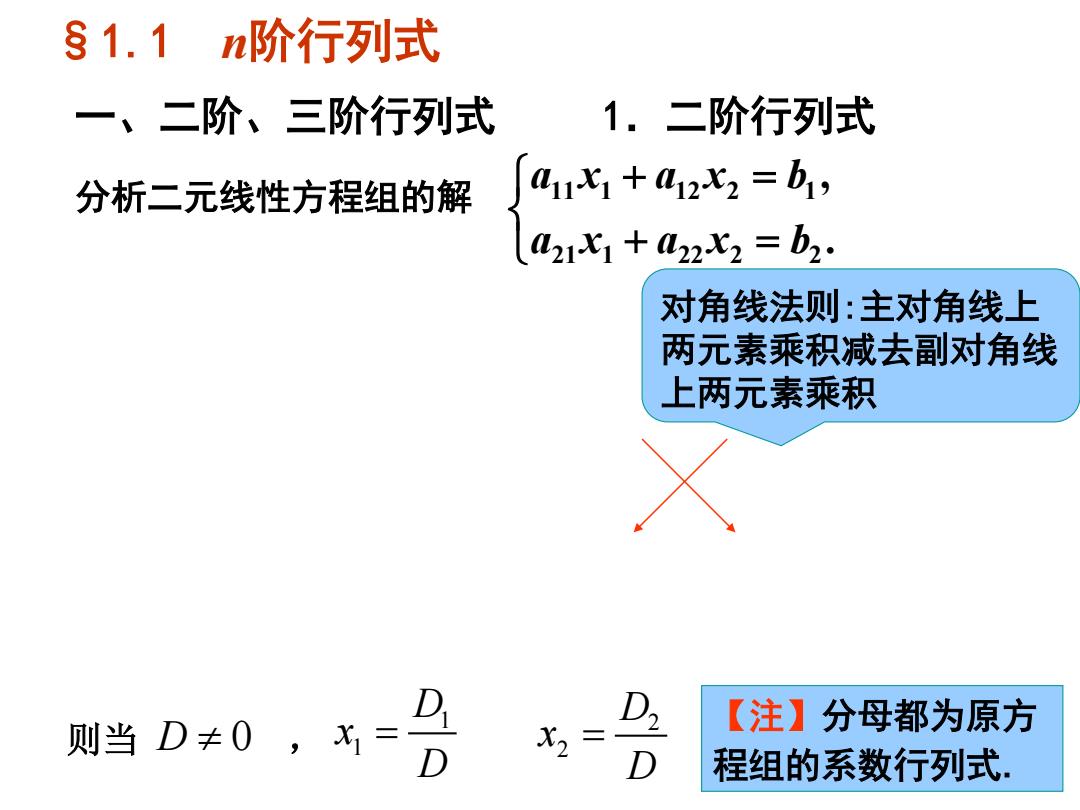
§1.1 n阶行列式 一、二阶、三阶行列式 1.二阶行列式 + = + = . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 分析二元线性方程组的解 1 1 D x D = 2 2 D x D 则当 D ≠ 0 , = 对角线法则:主对角线上 两元素乘积减去副对角线 上两元素乘积 【注】分母都为原方 程组的系数行列式

2x1+3x2=8 例1利用行列式解二元线性方程组 x1-2x2=-3 2 【练习】设D= 31 问入为何值时D=0,入为何值时D0?
【练习】设 2 3 1 D λ λ = 问λ为何值时D=0,λ为何值时D≠0? 例1 利用行列式解二元线性方程组 1 2 1 2 23 8 2 3 x x x x + = − =−

2.三阶行列式 411X1+4122+413X3=b1, 三元线性方程组了 21X1+022X2+23X3=b2, 431x1+432X2+4333=b3; 11 12 413 C12 13 应 D= a21 d22 a23 D1= b2 a22 C23 a31 a32 a33 b3 32 33 C11 b1 a13 C11 a12 D2=a21 b2 a23 D3= a21 22 b2 a31 b3 33 a31 a32 b3 希望当D≠0 也有 ,X2=D ,X3= D 问题 三阶行列式如何计算,使上面结论成立?
2.三阶行列式 希望当 D ≠ 0 也有 D D x D D x D D x 3 3 2 2 1 1 = , = , = + + = + + = + + = ; , , 31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b 问题 三阶行列式如何计算,使上面结论成立? 三元线性方程组 3 32 33 2 22 23 1 12 13 1 b a a b a a b a a 令 D = 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = 31 32 3 21 22 2 11 12 1 3 31 3 33 21 2 23 11 1 13 2 a a b a a b a a b D a b a a b a a b a D = =

三阶行列式的计算 =L112233+41223L31+4132132 -L13022L31-M1202133-411023L32 【注】1.红线上三元素的乘积冠以正号,蓝线上三元素的 乘积冠以负号. 2.三阶行列式包括3!项,每一项都是位于不同行,不同列的 三个元素的乘积,其中三项为正,三项为负. 1 2 3 例2计算 321=12 2 3 b 0 【练习】,b 满足什么条件时有 以上方法只适用于三阶行列式的计算
31 32 33 21 22 23 11 12 13 a a a a a a a a a = a11a22a33 . − a11a23a32 【注】1.红线上三元素的乘积冠以正号,蓝线上三元素的 乘积冠以负号. 2.三阶行列式包括3!项,每一项都是位于不同行,不同列的 三个元素的乘积,其中三项为正,三项为负. + a12a23a31 + a13a21a32 − a13a22a31 − a12a21a33 三阶行列式的计算 123 321 231 例2 计算 =12 【练习】a,b 满足什么条件时有 0 0 0 1 01 a b − = b a 以上方法只适用于三阶行列式的计算

x1-2x2+x3=-2 例3利用行列式解线性方程组{2x+x2一3x3=1 -x1+x2-x3=0 解 由于方程组的系数行列式
解 由于方程组的系数行列式 例3 利用行列式解线性方程组 12 3 1 23 12 3 2 2 2 31 0 xx x xxx xx x − + =− + −= −+ − =

n个未知数的线性方程组 : ax+a2x2+...+axn=b 2 a+a22x2+.+anxn=b2 D= 21 022 a amx+an2x2++ammxn=b n b b 12 a b 42 b2 D b2 022 02 02n b2 D a21 02n D : : .: : an2 an D 希望当 D≠0 .Xn D 问题对角线法则只适用于二阶与三阶行列式. n阶行列式如何计算使上述结论成立?
n个未知数的线性方程组 令 11 1 12 2 1 1 21 1 22 2 2 2 11 2 2 n n n n n n nn n n ax ax ax b ax a x ax b ax ax ax b + ++ = + ++ = + ++ = 11 12 1 21 22 2 1 2 n n n n nn aa a aa a D aa a = 1 12 1 2 22 2 1 2 n n n n nn ba a ba a D ba a = 11 1 1 21 2 2 2 1 n n n n nn ab a ab a D ab a = 11 12 1 21 22 2 1 2 n nn n aa b aa b D aa b = 问题 对角线法则只适用于二阶与三阶行列式. n阶行列式如何计算使上述结论成立? ... 希望当 1 2 1 2 , ,..., n n D D D xx x DD D = = = D ≠ 0

二、排列及其逆序数 定义1把n个不同的数排成一列,叫做这n个数的全排 列(或排列) 特别:由n个自然数1、2、..、n组成的有序数 组称为一个n级(阶、元)排列. n级排列共有n:种. 我们规定各数之间有一个标准次序,规定由小到大 为标准次序,若个不同的自然数按照由小到大排列,称 这样的排列为n元自然序排列. 定义2在一个排列(i2…i,…i,…i)中,若数i,>i, 则称这两个数构成一个逆序. 一个排列中所有逆序的总数称为此排列的逆序数, 记作t(i2…i…i…in)或N(2…i,…i…in)
二、排列及其逆序数 定义2 在一个排列 中,若数 则称这两个数构成一个逆序. ( ) t s n i i i i i 1 2 t s i > i 一个排列中所有逆序的总数称为此排列的逆序数, 记作 ( 1 2 ) ( 1 2 ). tsn tsn τ ii i i i N ii i i i 或 定义1 把n个不同的数排成一列,叫做这n个数的全排 列(或排列). 特别:由n个自然数1、2、…、n组成的有序数 组称为一个n级(阶、元)排列. n级排列共有n!种. 我们规定各数之间有一个标准次序,规定由小到大 为标准次序,若n个不同的自然数按照由小到大排列,称 这样的排列为n元自然序排列

求排列的逆序数两种思路 [方法一] 排列中比每一元素P大的且排在P:前面的元素个数 的总和T=T1+T2+…+Tm,即是这个排列的逆序数。 [方法二] 排列中比每一元素p:小的且排在p:后面的元素个数 ;的总和t=1十t2+…+Tn,也是这个排列的逆序数。 例如:求(32145) 【法一】 【法二】 3 2 1 4 5 3 2 1 4 5 ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ 0 1 2 0 2 1 0 x(32145) =3 (3 2145) =3
求排列的逆序数两种思路 排列中比每一元素 pi 大的且排在 前面的元素个数 i τ 1 2 n 的总和 ττ τ τ =+++ ,即是这个排列的逆序数。 i p [方法一] 排列中比每一元素 小的且排在 后面的元素个数 的总和 ,也是这个排列的逆序数。 i p i p i τ 1 2 n ττ τ τ =+++ [方法二] 例如:求 τ(32145) 32145 01200 τ 32145 3 ↓↓↓↓↓ ∴ 【法一】 ( )= 32145 21000 τ 32145 3 ↓↓↓↓↓ ∴ 【法二】 ( )=