
第1章函数极限连续 §1.1函数概念 ·§1.2常用经济函数 ·§1.3极限概念 ·§1.4极限的运算 ·§1.5无穷小量与无穷大量 ·§1.6函数连续 上页 返回
1 第1章 函数 极限 连续 • §1.1 函数概念 • §1.2 常用经济函数 • §1.3 极限概念 • §1.4 极限的运算 • §1.5 无穷小量与无穷大量 • §1.6 函数连续

§1.1函数概念 王王王王王王王王王 1.1.1函数的概念 1.常量与变量: 在某过程中数值保持不变的量称为常量, 而数值变化的量称为变量 通常用字母4,b,c等表示常量, 用字母x,y等表示变量 变量的取值范围称为变域。若为区间,则变量 是连续变量,否则为离散变量 如:物理中自由落体的距离与时间的关系为s-3, 其中变量的取值为(0,T),T为某个实数,t为连续变量, g=9.8m/s2,是重力加速度,是常量
2 1.常量与变量: 在某过程中数值保持不变的量称为常量, 通常用字母a, b, c等表示常量, 而数值变化的量称为变量. 变量的取值范围称为变域。若为区间,则变量 是连续变量,否则为离散变量. 用字母x, y, t等表示变量. 9.8 / , . (0, ), , , 2 1 2 0 0 2 = ,是重力加速度 是常量 其中变量 的取值为 为某个实数 为连续变量 如:物理中自由落体的距离 与时间 的关系为 , g m s t T T t s t s = gt §1.1 函数概念 1.1.1 函数的概念

2.区间与邻域 (1)区间 Ha,b∈R,且a<b {xa<x<b}称为开区间,记作(a,b) 0 L b x {xa≤x≤b}称为闭区间,记作[a,b] o a b 上页 返回
3 2.区间与邻域 ∀ a,b∈ R,且a < b. {x a < x < b} 称为开区间, 记作 (a,b) {x a ≤ x ≤ b} 称为闭区间, 记作[a,b] o a b x o a b x (1)区间

{xa≤x<b} 称为半开区间, 记作[a,b) {xa<x≤b} 称为半开区间,记作(a,b1 有限区间 [a,+oo)={xa≤x} (-o,b)={xx<b} 无限区间 L 有限区间长度的定义: 两端点间的距离(线段的长度)称为有限区间的长度 上贡 返回
4 {x a ≤ x < b} {x a < x ≤ b} 称为半开区间, 称为半开区间, 记作[a,b) 记作 (a,b] [a,+∞) = {x a ≤ x} (−∞,b) = {x x < b} o a x o b x 有限区间 无限区间 有限区间长度的定义: 两端点间的距离(线段的长度)称为有限区间的长度

(2) 邻域:设a与6是两个实数,且6>0. 数集{xx一a<6}称为点的邻域, 点称为该邻域的中心,6称为该邻域的半径· Os()={xa-<x<a+6}=(a-6,a+6), 6 M-δ L a+δ X 6 6 a-δ L a+δ X 上页 返回
5 (2)邻域:设a与δ是两个实数 , 且δ > 0. 点a称为该邻域的中心 , δ 称为该邻域的半径 . ( ) { δ δ } ( δ , δ ). Oδ a = x a − < x < a + = a − a + a − δ a a + δ x δ δ 数集{x x − a < δ }称为点a的δ邻域 , a − δ a a + δ x δ δ

点a的法心邻域,记作O,(a)八{} 0,(a)\a}={x0<x-d< (a-6,a)U(a,a+) a的左邻域的右邻域 有的书用如下记号: U(a,δ)=(a-6,a+δ); U(a,δ)=(a-6,m)U(a,a+6) 上页 返回
6 O (a) \{a}. 记作 δ 点a的δ去心邻域, ( , ) ( , ) ( ) \ { } { 0 } δ δ δ δ = − + = < − < a a a a O a a x x a a的左邻域 a的右邻域 ( , ) ( , ) ( , ); ( , ) ( , ); δ δ δ δ δ δ = − + = − + U a a a a a U a a a 。 有的书用如下记号:

土王 3.函数概念: 定义1.2设有两个变量x与y,D是一给定的非空实数集合 如果存在一个确定的法则(对应法则)∫,使得对每一个 x∈D,都有唯一的一个实数y与之对应,则称这个对应 法则为定义在实数集合D上的一个一元函数,简称 为函数.D称为的定义域,记为D(f) y 因变量 自变量 当x,∈D时,称yo=f(x)为函数在点x处的函数值, 也可记为yx=, 函数值全体组成的数集 R(f)={yy=f(x),x∈D(f)}称为函数的值域 返回
7 因变量 自变量 . , ( ) , 0 0 0 0 0 x x y x D y f x x = ∈ = 也可记为 当 时 称 为函数在点 处的函数值 ( ) { ( ), ( )}称为函数的值域. 函数值全体组成的数集 R f = y y = f x x∈ D f . , ( ). ( ) , 1.2 . D f D f f D x D y f x y D 为函数 称为 的定义域 记为 法则 为定义在实数集合 上的一个一元函数,简称 ,都有唯一的一个实数 与之对应,则称这个对应 如果存在一个确定的法则 对应法则 使得对每一个 定义 设有两个变量 与 , 是一给定的非空实数集合 ∈ y = f (x) 3.函数概念:

函数的两要素:定义域与对应法则 D Xo) 对应法则力 自变量 R f(xo) 因变量 约定:定义域是自变量所能取的使算式有意义的一 切实数值,在实际背景的函数中的按实际意义确定 例如,y= D:(-1,1) W1-x2 两个函数相同一定义域和对应法则均相同 y= x2-2x+1 与y=x-1不同 x-1 4.函数表示法:解析法、表格法和图形法 8返回
8 ( ( ) ) x0 ( ) x0 f 自变量 因变量 对应法则f 函数的两要素: 定义域与对应法则. x y D R 约定: 定义域是自变量所能取的使算式有意义的一 切实数值,在实际背景的函数中的按实际意义确定. 2 1 1 x y − 例如, = D :(−1,1) 两个函数相同 ⇔ 定义域和对应法则均相同 与 1不同 1 2 1 2 = − − − + = y x x x x y 4.函数表示法:解析法、表格法和图形法

例1求函数y=√16-x2+Igsinx的定义域 上页 下页 返回
9 例1 16 lg sin . 求函数 y = − x2 + x 的定义域
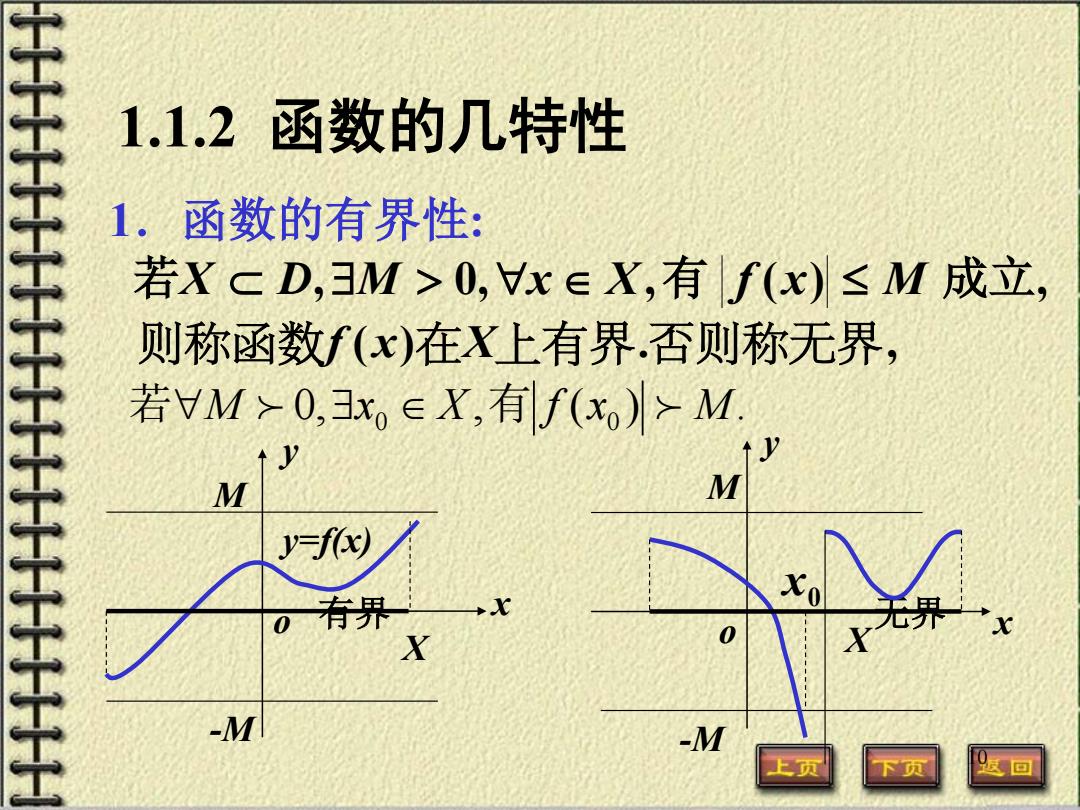
1.1.2函数的几特性 1.函数的有界性: 若XcD,3M>0,x∈X,有f(x)≤M成立, 则称函数f(x)在X上有界否则称无界, 若M>0,x∈X,有f(x)>M ↑y M M yf岁) 一田 Xo 0下 .x X X -M -M 返回
10 1.1.2 函数的几特性 M -M y x o y=f(x) X 有界 无界 M -M y o x X x0 若X ⊂ D,∃M > 0,∀x ∈ X,有 f (x) ≤ M 成立, 1.函数的有界性: 则称函数f (x)在X上有界.否则称无界, 0, , ( ) . 若∀M ∃x0 ∈ X 有 f x0 M