
第2章一元函数微分学 §2.1导数的概念 ·§2.2导数的运算法则与基本公式 §2.3高阶导数 ·§2.4微分及其计算 ·§2.5中值定理罗比塔法则 ·§2.6函数的单调性与极值 §2.7微分在经济中的应用 上页 返回
1 第2章 一元函数微分学 • §2.1 导数的概念 • §2.2 导数的运算法则与基本公式 • §2.3 高阶导数 • §2.4 微分及其计算 • §2.5 中值定理 罗比塔法则 • §2.6 函数的单调性与极值 • §2.7 微分在经济中的应用
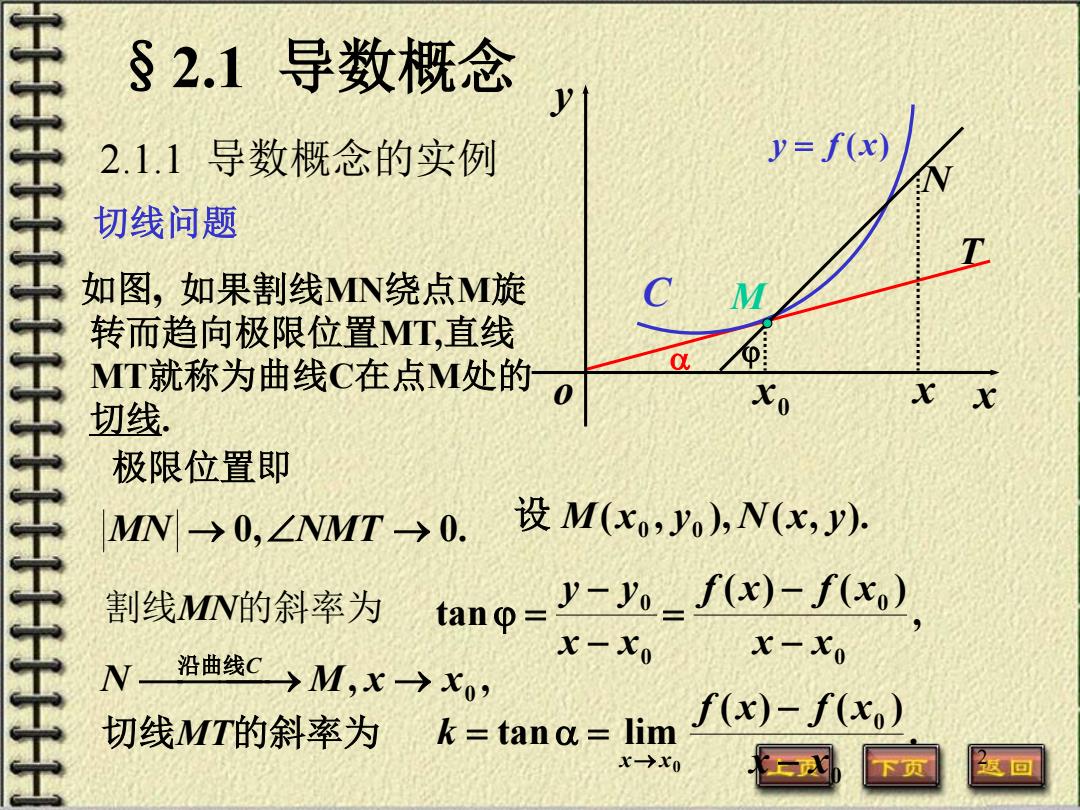
§2.1导数概念 2.1.1导数概念的实例 y=f 切线问题 如图,如果割线MN绕点M旋 转而趋向极限位置T,直线 MT就称为曲线C在点M处的 X x 切线 极限位置即 MN→0,∠NMT→0. 设M(xo,yo),N(x,y) 割线MN的斜率为 tano= y-Yo_f(x)-f(xo) x-xo x-xo N 沿曲线C)M,X→Xo, 切线MT的斜率为 k=tan a=lim f(x)-f(xo) x→x0 返回
2 α ϕ T x0 o x x y y = f (x) C N 如图, 如果割线MN绕点M旋 M 转而趋向极限位置MT,直线 MT就称为曲线C在点M处的 切线. 极限位置即 MN → 0,∠NMT → 0. ( , ), ( , ). 0 0 设 M x y N x y 割线MN的斜率为 0 0 tan x x y y − − ϕ = , ( ) ( ) 0 0 x x f x f x − − = , , N M x x0 沿曲线 C → → 切线MT的斜率为 . ( ) ( ) tan lim 0 0 0 x x f x f x k x x − − = α = → 切线问题 §2.1 导数概念 2.1.1 导数概念的实例

2.1.2导数的定义 定义2.1 设函数y=f(x)在点x的某个邻域内 有定义,当自变量x在x,处取得增量△x(点 x,+△x仍在该邻域内时,相应地函数y取 得增量△y=f(x,+△x)-f(x);如果△y与 △x之比当△x→0时的极限存在则称函数 y=f(x)在点x处可导,并称这个极限为函 数y=f(x)在点x处的导数记为f'(xy-, 上贡 返回
3 2.1.2 导数的定义 ( ) , ( ), , ( ) , 0 , ( ) ( ); ) , , ( ( ) 0 0 0 0 0 0 0 0 0 x x y f x x f x y y f x x x x y f x x f x y x x y x x x y f x x = = ′ ′ = ∆ ∆ → ∆ = + ∆ − ∆ + ∆ ∆ = 数 在点 处的导数 记为 在点 处可导 并称这个极限为函 之比当 时的极限存在 则称函数 得增量 如果 与 仍在该邻域内时 相应地函数 取 有定义 当自变量 在 处取得增量 点 设函数 在点 的某个邻域内 定义2.1

或 (x) dx =x0) 即'x)= Ay=tim f(x+△r)-f(x) Ax-→0△x △x→0 △x 其它形式 f,)= f(xo+h)-f(xo) h f(xo)=lim f(x)-f(xo) x-→x0 x-xo (只须令x=x,+△x,则△x→0,x→x) 上页 页 返回
4 . ( ) ( ) ( ) lim 0 0 0 0 h f x h f x f x h + − ′ = → 其它形式 . ( ) ( ) ( ) lim 0 0 0 0 x x f x f x f x x x − − ′ = → x f x x f x x y f x x x ∆ + ∆ − = ∆ ∆ ′ = ∆ → ∆ → ( ) ( ) ( ) lim lim 0 0 0 0 0 , ( ) 0 0 x x x x dx df x dx dy = 或 = 即 ( , 0, ) 只须令x = x0 + ∆x 则∆x → x → x0

★对于任一x∈I,都对应着f(x)的一个确定的 导数值这个函数叫做原来函数f(x)的导函数 记作y,f'x,或(四 d dx 即y'=lim f(x+△x)-f(x) △x-→0 △x 或f'(x)=1ime+月-fx) h0 h 注:1.f'(x)=f'(x)- 2.导函数(瞬时变化率)是函数平均变化率 的逼近函数. 上页 返回
5 x f x x f x y x ∆ + ∆ − ′ = ∆ → ( ) ( ) lim 0 即 . ( ) ( ) ( ) lim 0 h f x h f x f x h + − ′ = → 或 注: 1. ( ) ( ) . 0 x x0 f x f x = ′ = ′ ★ 2.导函数(瞬时变化率)是函数平均变化率 的逼近函数. . ( ) , ( ), . ( ) . , ( ) dx df x dx dy y f x f x x I f x 记作 或 导数值 这个函数叫做原来函数 的导函数 对于任一 都对应着 的一个确定的 ′ ′ ∈

例1 设函数f(x)=sinx,求(sinx)'及(sinx)' 上页 下页 返回
6 例1 ( ) sin , (sin ) (sin ) . 4 π = = ′ ′ x 设函数 f x x 求 x 及 x 解

★定义2.3单侧导数 1.左导数: f(xo)=lim f(x)-f(xo) lim f(x+△)-fx: x-xo △x→0 △x 2.右导数: (xo)=lim fw)-fx)=lim f(x+△x)-f(xo) x→x0 x-xo △x→0+ △x ★函数fx)在点x,处可导一左导数f(x)和右导 数f(x。)都存在且相等. ★如果f(x)在开区间(a,b)内可导,且f(a)及 '(b)都存在,就说f(x)在闭区间[a,b上可导 上页 返回
7 ★ 2.右导数: 定义2.3 单侧导数 1.左导数: ; ( ) ( ) lim ( ) ( ) ( ) lim 0 0 0 0 0 0 0 x f x x f x x x f x f x f x x x x ∆ + ∆ − = − − ′ = − → − → ∆ − ; ( ) ( ) lim ( ) ( ) ( ) lim 0 0 0 0 0 0 0 x f x x f x x x f x f x f x x x x ∆ + ∆ − = − − ′ = + → + → ∆ + 函数 f (x)在点x0处可导⇔左导数 ( ) x0 f − ′ 和右导 数 ( ) x0 f + ′ 都存在且相等. ★ ★ 如果 f (x)在开区间(a,b)内可导,且 f (a) + ′ 及 f (b) − ′ 都存在,就说 f (x)在闭区间[a,b]上可导

例2 讨论函数f(x)=x在x=0处的可导性. 解 上页 下页 返回
8 例2 讨论函数 f (x) = x 在x = 0处的可导性. 解

2.1.3可导与连续的关系 定理2.1若f(x)在x,点可导,则f(x)在x点连续 证 设函数f(x)在点x,可导, lim A=f(x) Ax-→0△X lim Ay=lim △x-→0 Ay.△x=f'x)0=0 Ax→0△x .函数f(x)在点x连续 注:连续是可导的必要非充分条件,即连续 函数并不一定可导,但不连续函数必不可导. 上贡 返回
9 定理 2.1 证 ( ) , 设函数 f x 在点 x0可导 lim ( ) 0 0 f x x y x = ′ ∆ ∆ ∆ → 0 0 0 0 0 ⋅∆ = ′ ⋅ = ∆ ∆ ∆ = ∆ → ∆ → lim lim x f (x ) x y y x x 函数 ( )在点 连续 . 0 ∴ f x x 注: 连续是可导的必要非充分条件,即连续 函数并不一定可导,但不连续函数必不可导. 若 ( )在 点可导,则 ( )在 点连续. 0 0 f x x f x x 2.1.3 可导与连续的关系
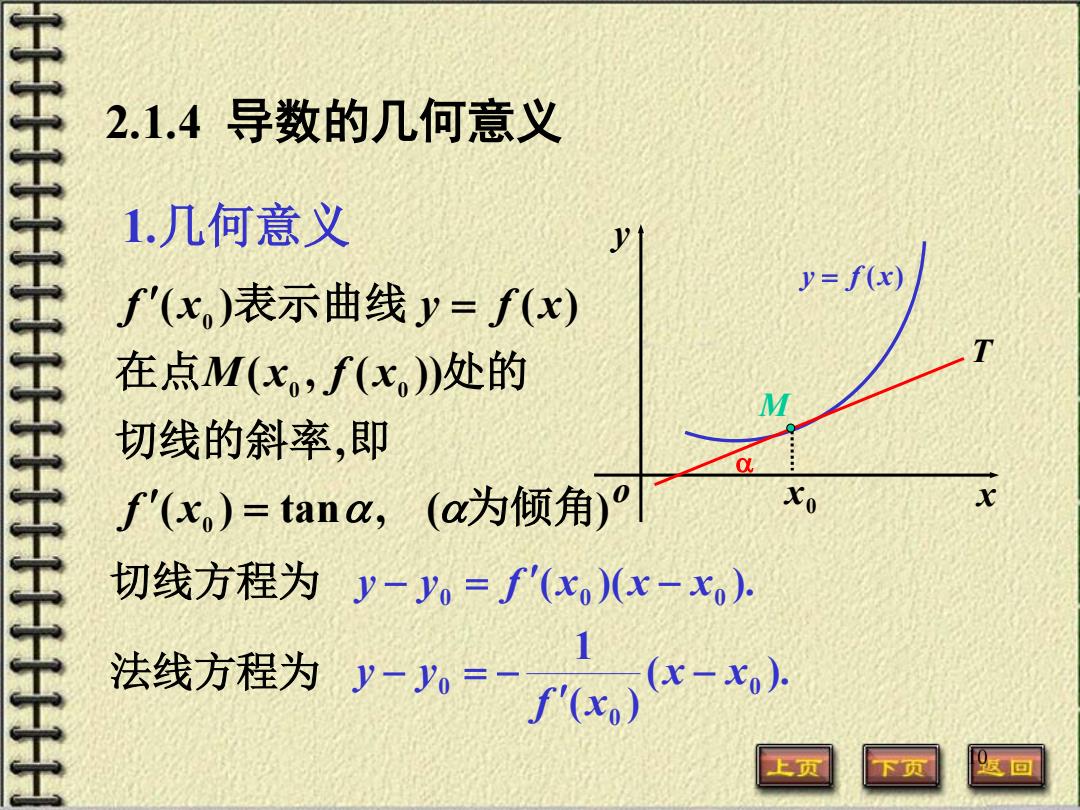
2.1.4导数的几何意义 1.几何意义 f'(x,)表示曲线y=f(x) Y-f(x) T 在点M(x,f(x。)处的 M 切线的斜率,即 f'(x,)=tana,(a为倾角)° Xo X 切线方程为y-y,=f'(x)(x一x) 法线程为y-f代 上页 9返回
10 2.1.4 导数的几何意义 o x y y = f (x) α T x0 M 1.几何意义 ( ) tan , ( ) , ( , ( )) ( ) ( ) 0 0 0 0 为倾角 切线的斜率 即 在点 处的 表示曲线 ′ = α α ′ = f x M x f x f x y f x 切线方程为 法线方程为 ( )( ). 0 x0 x x0 y − y = f ′ − ( ). ( ) 1 0 0 0 x x f x y y − ′ − = −