
二元盖热微积分 一元函数微分学 推广 二元函数微分学 注意:善于类比,区别异同
推广 一元函数微分学 二元函数微分学 注意: 善于类比, 区别异同 二元函数微积分

二元高数的基本橇念 一、区域 二、二元函数的概念
一、区域 二、二元函数的概念 二元函数的基本概念
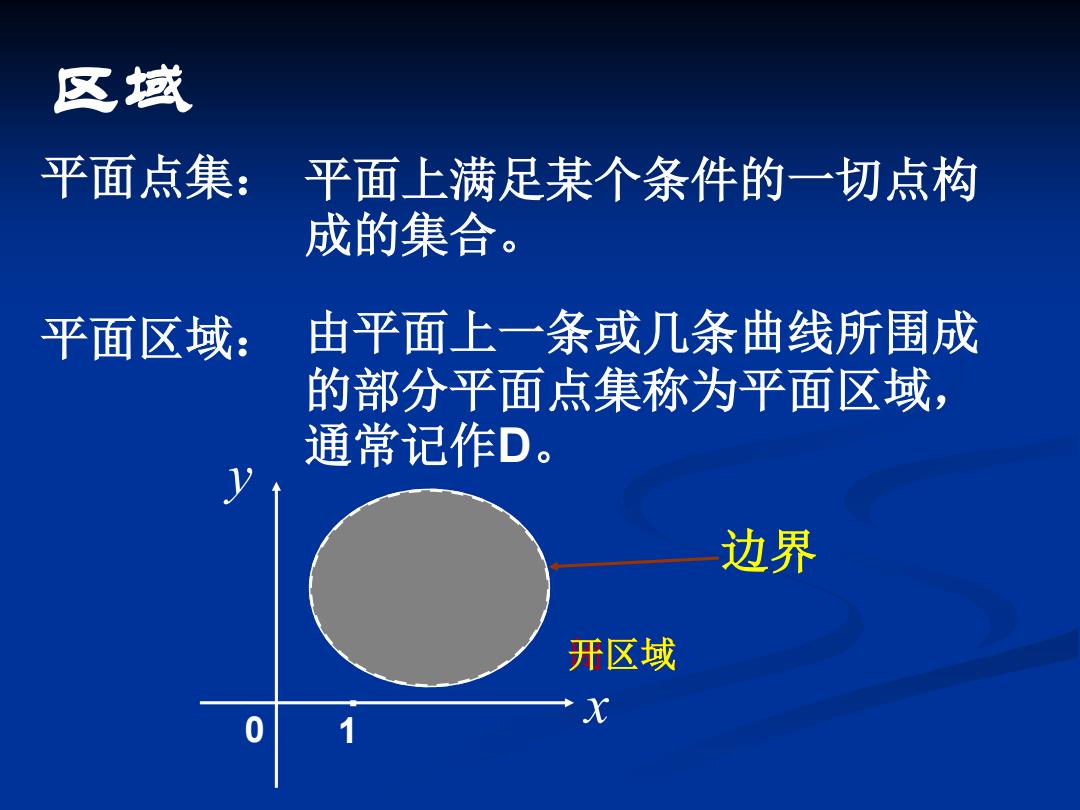
区域 平面点集:平面上满足某个条件的一切点构 成的集合。 平面区域: 由平面上一条或几条曲线所围成 的部分平面点集称为平面区域, 通常记作D。 边界 开区域 X
区域 平面上满足某个条件的一切点构 成的集合。 平面点集: 平面区域: 由平面上一条或几条曲线所围成 的部分平面点集称为平面区域, 通常记作D。 0 x y 1 · 边界 闭区域 开

常见区域 y=P2(x) x=P2(r) y=g(x) 0 a 0 x 文型区域 Y型区域 由x=ax=b 由y=cy=d y=02(x)y=0(x) x=0(Jy)x=02(y) 四条曲线围成 四条曲线围成
0 x y ( ) 1 y =ϕ x ( ) 2 y =ϕ x a b 0 x y c d ( ) 1 x =ϕ y ( ) 2 x =ϕ y X 型区域 Y 型区域 常见区域 x = a x = b ( ) 1 ( ) y =ϕ x 2 y =ϕ x 由 四条曲线围成 由 y = c y = d 四条曲线围成 ( ) 1 x =ϕ y ( ) 2 x =ϕ y

邻域: 平面上以点P(x,y)为圆心,6>0为半径的圆内部构成 的开区-{红,y小(x-x广+0-厂0称 为点(xo,yo)的δ邻域。 Po (Xo-Yo) 0 x
邻域: 平面上以点 ( , ) 0 0 0 P x y 为圆心,δ > 0 为半径的圆内部构成 的有界开区域 {( , ) ( ) ( ) , 0} 2 0 2 D = x y x − x0 + y − y 称 为点 ( , ) 0 0 0 P x y 的δ 邻域。 0 x y 1 · • δ ( , ) 0 0 0 P x y

二元函数的概念 定义:设有三个变量x,y和z,如果当变量x,y 在平面区域D为任取一组值时,变量z按照一定的规 律f,总有唯一确定的数值与之对应,则称z为x,y的 二元函数,记作z=f(x,y),其中x,y称为自变量, 函数z也称为因变量,x,y的变化范围D称为函数的定 义域。 类似的,可以定义三元函数=f(x,y,z)及三元以上的函数
定义:设有三个变量 x, y 和 z ,如果当变量 x, y 在某平面区域 D 内任取一组值时,变量 z 按照一定的规 律 f ,总有唯一确定的数值与之对应,则称 z 为 x, y 的 二元函数,记作 z = f (x, y) ,其中 x, y 称为自变量, 函数 z 也称为因变量,x, y 的变化范围 D 称为函数的定 义域。 类似的,可以定义三元函数u = f (x, y,z) 及三元以上的函数。 二元函数的概念

自变量个数 定义域 一元函数 一个:X 在数轴上讨论 (区间) 二元函数两个:x,y 在平面上讨论 (区域)
一元函数 二元函数 自变量个数 定义域 一个:x 两个:x, y 在数轴上讨论 (区间) 在平面上讨论 (区域)

偏导数 一、偏导数概念及其计算 二、高阶偏导数
一、 偏导数概念及其计算 二 、高阶偏导数 偏导数

定义:设函数z=f(x,y)在点(xo,y0) 的某邻域内 极限 lim f(xo+△x,yo)-f(x,yo) x→0 △x 存在,则称此极限为函数z=f(x,y)在点(x,yo)对x 的偏导数,记为 0z ax(x0,y0)”ax(xo,yo) 2x(x0,0) f(xo,yo);f(xo,yo) 注意:f(x,)1m f(x0+△x,0)-f(x0,o》 △x-→0 △x dx(.)x-x
定义: z = f (x, y)在点 存在, z f (x, y) 在点(x , y ) 对x = 0 0 的偏导数,记为 ( , ) 0 0 x y 的某邻域内 ; ( , ) 0 0 x x y f ∂ ∂ x + ∆x 0 0x 则称此极限为函数 极限 设函数 ∆x ; ( , ) 0 0 x x y z x f x x y f x y x ∆ + ∆ − = ∆ → ( , ) ( , ) lim 0 0 0 0 0 ( , ) 0 0 f x y x 注意: ′

同样可定义对y的偏导数 f(oo)=lim f(x0,o+△y)-f(x0,0) △y-→0 △y f(x0,)= 若函数z=f(x,y)在域D内每一点(x,y)处对x 或y偏导数存在,则该偏导数称为偏导函数,也简称为 偏导数,记为 of ,2x,f(xy),(x,y) 部m.n
同样可定义对 y 的偏导数 lim ∆ →0 = y ( , ) 0 0 f x y y ′ 若函数 z = f ( x , y ) 在域 D 内每一点 ( x , y ) 处对 x 则该偏导数称为偏导函数, 也简称为 偏导数 , ( , ) , ( , ) 2 f x y f x y y ′ ′ ( , ) 0 f x ( , ) 0 − f x ∆y 记为 y + ∆y 0 0 y 或 y 偏导数存在 , , , , y z y f y z ∂ ∂ ∂ ∂