
第二章、经典单方程计量经济学模型:多元线性回归模型 一、内容提要 本章将一元回归模型拓展到了多元回归模型,其基本的建模思想与建模方法与一元的 情形相同。主要内容仍然包括模型的基本假定、模型的估计、模型的检验以及模型在预测方 面的应用等方面。只不过为了多元建模的需要,在基本假设方面以及检验方面有所扩充。 本章仍重点介绍了多元线性回归模型的基本假设、估计方法以及检验程序。与一元回 归分析相比,多元回归分析的基本假设中引入了多个解释变量间不存在(完全)多重共线性 这一假设:在检验部分,一方面引入了修正的可决系数,另一方面引入了对多个解释变量是 否对被解释变量有显著线性影响关系的联合性F检验,并讨论了F检验与拟合优度检验的 内在联系。 本章的另一个重点是将线性回归模型拓展到非线性回归模型,主要学习非线性模型如 何转化为线性回归模型的常见类型与方法。这里需要注意各回归参数的具体经济含义。 本章第三个学习重点是关于模型的约束性检验问题,包括参数的线性约束与非线性约 束检验。参数的线性约束检验包括对参数线性约束的检验、对模型增加或减少解释变量的检 验以及参数的稳定性检验三方面的内容,其中参数稳定性检验又包括邹氏参数稳定性检验与 邹氏预测检验两种类型的检验。检验都是以F检验为主要检验工具,以受约束模型与无约 束模型是否有显著差异为检验基点。参数的非线性约束检验主要包括最大似然比检验、沃尔 德检验与拉格朗日乘数检验。它们仍以估计无约束模型与受约束模型为基础,但以最大似然 原理进行估计,且都适用于大样本情形,都以约束条件个数为自由度的X分布为检验统计 量的分布特征。非线性约束检验中的拉格朗日乘数检验在后面的章节中多次使用。 二、典型例题分析 例1.某地区通过一个样本容量为722的调查数据得到劳动力受教育的一个回归方程为 Y=10.36-0.094X1+0.131X2+0.210X3 R2=0.214 式中,Y为劳动力受教育年数,X为该劳动力家庭中兄弟姐妹的个数,X,与X,分别为母
第二章、经典单方程计量经济学模型:多元线性回归模型 一、内容提要 本章将一元回归模型拓展到了多元回归模型,其基本的建模思想与建模方法与一元的 情形相同。主要内容仍然包括模型的基本假定、模型的估计、模型的检验以及模型在预测方 面的应用等方面。只不过为了多元建模的需要,在基本假设方面以及检验方面有所扩充。 本章仍重点介绍了多元线性回归模型的基本假设、估计方法以及检验程序。与一元回 归分析相比,多元回归分析的基本假设中引入了多个解释变量间不存在(完全)多重共线性 这一假设;在检验部分,一方面引入了修正的可决系数,另一方面引入了对多个解释变量是 否对被解释变量有显著线性影响关系的联合性 F 检验,并讨论了 F 检验与拟合优度检验的 内在联系。 本章的另一个重点是将线性回归模型拓展到非线性回归模型,主要学习非线性模型如 何转化为线性回归模型的常见类型与方法。这里需要注意各回归参数的具体经济含义。 本章第三个学习重点是关于模型的约束性检验问题,包括参数的线性约束与非线性约 束检验。参数的线性约束检验包括对参数线性约束的检验、对模型增加或减少解释变量的检 验以及参数的稳定性检验三方面的内容,其中参数稳定性检验又包括邹氏参数稳定性检验与 邹氏预测检验两种类型的检验。检验都是以 F 检验为主要检验工具,以受约束模型与无约 束模型是否有显著差异为检验基点。参数的非线性约束检验主要包括最大似然比检验、沃尔 德检验与拉格朗日乘数检验。它们仍以估计无约束模型与受约束模型为基础,但以最大似然 原理进行估计,且都适用于大样本情形,都以约束条件个数为自由度的 2 χ 分布为检验统计 量的分布特征。非线性约束检验中的拉格朗日乘数检验在后面的章节中多次使用。 二、典型例题分析 例 1.某地区通过一个样本容量为 722 的调查数据得到劳动力受教育的一个回归方程为 1 2 210 3 Y = 10.36 − 0.094X + 0.131X + 0. X R2 =0.214 式中,Y 为劳动力受教育年数,X1为该劳动力家庭中兄弟姐妹的个数,X 2 与 X3分别为母

亲与父亲受到教育的年数。问 (1)X,是否具有预期的影响?为什么?若X,与X,保持不变,为了使预测的受教育水 平减少一年,需要X,增加多少? (2)请对X2的系数给予适当的解释。 (3)如果两个劳动力都没有兄弟姐妹,但其中一个的父母受教育的年数为12年,另一 个的父母受教育的年数为16年,则两人受教育的年数预期相差多少? 解答: (1)预期X,对劳动者受教育的年数有影响。因此在收入及支出预算约束一定的条件下, 子女越多的家庭,每个孩子接受教育的时间会越短。 根据多元回归模型偏回归系数的含义,X,前的参数估计值-0.094表明,在其他条件不 变的情况下,每增加1个兄弟姐妹,受教育年数会减少0.094年,因此,要减少1年受教育 的时间,兄弟姐妹需增加1/0.094=10.6个。 (2)X,的系数表示当兄弟姐妹数与父亲受教育的年数保持不变时,母亲每增加1年 受教育的机会,其子女作为劳动者就会预期增加0.131年的受教育机会。 (3)首先计算两人受教育的年数分别为 10.36+0.131×12+0.210×12=14.452 10.36+0.131×16+0.210×16=15.816 因此,两人的受教育年限的差别为15.816-14.452=1.364 例2.以企业研发支出(R&D)占销售额的比重为被解释变量(Y),以企业销售额(X,) 与利润占销售额的比重(X,)为解释变量,一个有32容量的样本企业的估计结果如下: Y=0.472+0.321og(X,)+0.05X2 (1.37)(0.22) (0.046) R2=0.099 其中括号中为系数估计值的标准差。 (1)解释log(X)的系数。如果X,增加10%,估计Y会变化多少个百分点?这在经济 上是一个很大的影响吗? (2)针对R&D强度随销售额的增加而提高这一备择假设,检验它不随X,而变化的假 设。分别在5%和10%的显著性水平上进行这个检验。 (3)利润占销售额的比重X,对R&D强度Y是否在统计上有显著的影响? 解答: (1)log(X,)的系数表明在其他条件不变时,1og(X)变化1个单位,Y变化的单位数
亲与父亲受到教育的年数。问 (1)X1是否具有预期的影响?为什么?若 X 2 与 X3保持不变,为了使预测的受教育水 平减少一年,需要 X1增加多少? (2)请对 X 2 的系数给予适当的解释。 (3)如果两个劳动力都没有兄弟姐妹,但其中一个的父母受教育的年数为 12 年,另一 个的父母受教育的年数为 16 年,则两人受教育的年数预期相差多少? 解答: (1)预期 X1对劳动者受教育的年数有影响。因此在收入及支出预算约束一定的条件下, 子女越多的家庭,每个孩子接受教育的时间会越短。 根据多元回归模型偏回归系数的含义, X1前的参数估计值-0.094 表明,在其他条件不 变的情况下,每增加 1 个兄弟姐妹,受教育年数会减少 0.094 年,因此,要减少 1 年受教育 的时间,兄弟姐妹需增加 1/0.094=10.6 个。 (2) X 2 的系数表示当兄弟姐妹数与父亲受教育的年数保持不变时,母亲每增加 1 年 受教育的机会,其子女作为劳动者就会预期增加 0.131 年的受教育机会。 (3)首先计算两人受教育的年数分别为 10.36+0.131×12+0.210×12=14.452 10.36+0.131×16+0.210×16=15.816 因此,两人的受教育年限的差别为 15.816-14.452=1.364 例 2.以企业研发支出(R&D)占销售额的比重为被解释变量(Y ),以企业销售额( X1) 与利润占销售额的比重( X 2 )为解释变量,一个有 32 容量的样本企业的估计结果如下: 0.099 (1.37) (0.22) (0.046) 0.472 0.32log( ) 0.05 2 1 2 = = + + R Y X X 其中括号中为系数估计值的标准差。 (1)解释 log( X1 )的系数。如果 X1增加 10%,估计Y 会变化多少个百分点?这在经济 上是一个很大的影响吗? (2)针对 R&D 强度随销售额的增加而提高这一备择假设,检验它不随 X1而变化的假 设。分别在 5%和 10%的显著性水平上进行这个检验。 (3)利润占销售额的比重 X 2 对 R&D 强度Y 是否在统计上有显著的影响? 解答: (1)log( X1 )的系数表明在其他条件不变时,log( X1 )变化 1 个单位,Y 变化的单位数
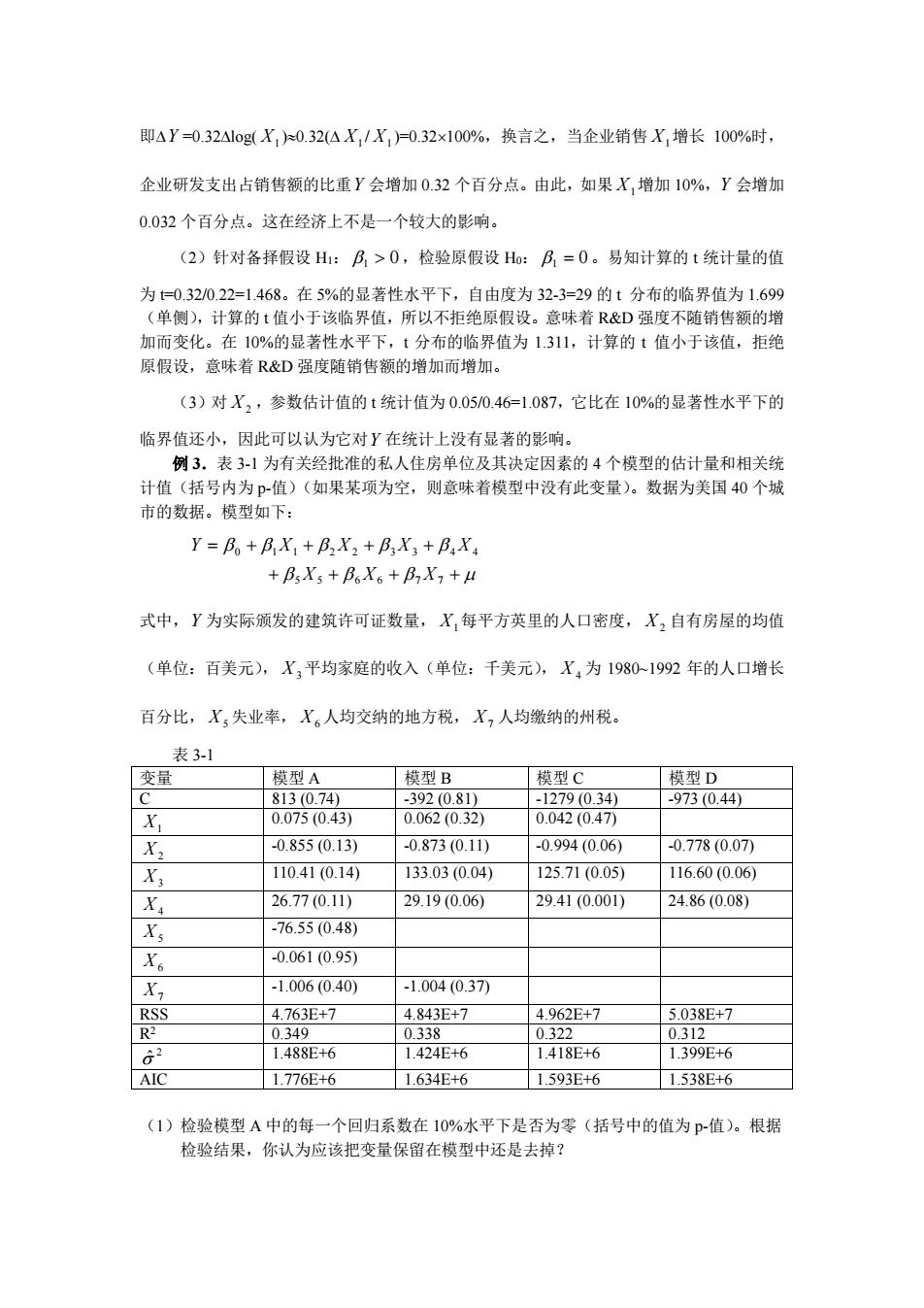
即△Y=0.32△l0g(X,)0.32(△X,/X,)=0.32×100%,换言之,当企业销售X,增长100%时, 企业研发支出占销售额的比重Y会增加0.32个百分点。由此,如果X,增加10%,Y会增加 0.032个百分点。这在经济上不是一个较大的影响。 (2)针对备择假设H:B,>0,检验原假设Ho:B,=0。易知计算的t统计量的值 为=0.32/0.22=1.468。在5%的显著性水平下,自由度为32-3=29的t分布的临界值为1.699 (单侧),计算的t值小于该临界值,所以不拒绝原假设。意味着R&D强度不随销售额的增 加而变化。在10%的显著性水平下,t分布的临界值为1.311,计算的t值小于该值,拒绝 原假设,意味着R&D强度随销售额的增加而增加。 (3)对X2,参数估计值的t统计值为0.05/0.46=1.087,它比在10%的显著性水平下的 临界值还小,因此可以认为它对Y在统计上没有显著的影响。 例3.表3-1为有关经批准的私人住房单位及其决定因素的4个模型的估计量和相关统 计值(括号内为p-值)(如果某项为空,则意味着模型中没有此变量)。数据为美国40个城 市的数据。模型如下: Y=Bo+Bx+Bx2+Bx3+BX +BX5+B6X6+B,X,+4 式中,Y为实际颁发的建筑许可证数量,X,每平方英里的人口密度,X,自有房屋的均值 (单位:百美元),X,平均家庭的收入(单位:千美元),X4为1980-1992年的人口增长 百分比,X,失业率,X。人均交纳的地方税,X,人均缴纳的州税。 表3-1 变量 模型A 模型B 模型C 模型D C 813(0.74) -392(0.81) -1279(0.34) -973(0.44) X 0.075(0.43) 0.062(0.32) 0.042(0.47 X2 -0.855(0.13) -0.873(0.11) -0.994(0.06) -0.778(0.07 X3 110.41(0.14) 133.03(0.04) 125.71(0.05) 116.60(0.06) X 26.77(0.11) 29.19(0.06) 29.41(0.001) 24.86(0.08) X -76.55(0.48) Xo -0.061(0.95) X -1.006(0.40) -1.004(0.37 RSS 4.763E+7 4.843E+7 4.962E+7 5.038E+7 R2 0.349 0.338 0.322 0.312 62 1.488E+6 1.424E+6 1.418E+6 1.399E+6 AIC 1.776E+6 1.634E+6 1.593E+6 1.538E+6 (1)检验模型A中的每一个回归系数在10%水平下是否为零(括号中的值为p-值)。根据 检验结果,你认为应该把变量保留在模型中还是去掉?
即∆Y =0.32∆log( X1 )≈0.32(∆ X1 / X1 )=0.32×100%,换言之,当企业销售 X1增长 100%时, 企业研发支出占销售额的比重Y 会增加 0.32 个百分点。由此,如果 X1增加 10%,Y 会增加 0.032 个百分点。这在经济上不是一个较大的影响。 (2)针对备择假设 H1: β1 > 0 ,检验原假设 H0: β1 = 0。易知计算的 t 统计量的值 为 t=0.32/0.22=1.468。在 5%的显著性水平下,自由度为 32-3=29 的 t 分布的临界值为 1.699 (单侧),计算的 t 值小于该临界值,所以不拒绝原假设。意味着 R&D 强度不随销售额的增 加而变化。在 10%的显著性水平下,t 分布的临界值为 1.311,计算的 t 值小于该值,拒绝 原假设,意味着 R&D 强度随销售额的增加而增加。 (3)对 X 2 ,参数估计值的 t 统计值为 0.05/0.46=1.087,它比在 10%的显著性水平下的 临界值还小,因此可以认为它对Y 在统计上没有显著的影响。 例 3.表 3-1 为有关经批准的私人住房单位及其决定因素的 4 个模型的估计量和相关统 计值(括号内为 p-值)(如果某项为空,则意味着模型中没有此变量)。数据为美国 40 个城 市的数据。模型如下: β β β µ β β β β β + + + + = + + + + 5 5 6 6 7 7 0 1 1 2 2 3 3 4 4 X X X Y X X X X 式中,Y 为实际颁发的建筑许可证数量, X1每平方英里的人口密度, X 2 自有房屋的均值 (单位:百美元), X3平均家庭的收入(单位:千美元), X 4 为 1980~1992 年的人口增长 百分比, X5失业率, X6人均交纳的地方税, X7 人均缴纳的州税。 表 3-1 变量 模型 A 模型 B 模型 C 模型 D C 813 (0.74) -392 (0.81) -1279 (0.34) -973 (0.44) X1 0.075 (0.43) 0.062 (0.32) 0.042 (0.47) X 2 -0.855 (0.13) -0.873 (0.11) -0.994 (0.06) -0.778 (0.07) X3 110.41 (0.14) 133.03 (0.04) 125.71 (0.05) 116.60 (0.06) X 4 26.77 (0.11) 29.19 (0.06) 29.41 (0.001) 24.86 (0.08) X5 -76.55 (0.48) X6 -0.061 (0.95) X7 -1.006 (0.40) -1.004 (0.37) RSS 4.763E+7 4.843E+7 4.962E+7 5.038E+7 R2 0.349 0.338 0.322 0.312 2 σˆ 1.488E+6 1.424E+6 1.418E+6 1.399E+6 AIC 1.776E+6 1.634E+6 1.593E+6 1.538E+6 (1)检验模型 A 中的每一个回归系数在 10%水平下是否为零(括号中的值为 p-值)。根据 检验结果,你认为应该把变量保留在模型中还是去掉?

(2)在模型A中,在10%水平下检验联合假设H0:B,=0(i=1,5,6,7)。说明被择假设,计 算检验统计值,说明其在零假设条件下的分布,拒绝或接受零假设的标准。说明你的 结论。 (3)哪个模型是“最优的”?解释你的选择标准。 (4)说明最优模型中有哪些系数的符号是“错误的”。说明你的预期符号并解释原因。确认 其是否为正确符号。 解答: (1)直接给出了p一值,所以没有必要计算t~统计值以及查t分布表。根据题意,如果p 值0,事实上其估 计值确是大于零的。同样地,随着人口的增加,住房需求也会随之增加,所以我们预期B4>0, 事实上其估计值也是如此。随着房屋价格的上升,我们预期对住房的需求人数减少,即我们 预期B,估计值的符号为负,回归结果与直觉相符。出乎预料的是,地方税与州税为不显著 的。由于税收的增加将使可支配收入降低,所以我们预期住房的需求将下降。虽然模型A 是这种情况,但它们的影响却非常微弱。 例4、在经典线性模型基本假定下,对含有三个自变量的多元回归模型:
(2)在模型 A 中,在 10%水平下检验联合假设 H0:β i =0(i=1,5,6,7)。说明被择假设,计 算检验统计值,说明其在零假设条件下的分布,拒绝或接受零假设的标准。说明你的 结论。 (3)哪个模型是“最优的”?解释你的选择标准。 (4)说明最优模型中有哪些系数的符号是“错误的”。说明你的预期符号并解释原因。确认 其是否为正确符号。 解答: (1)直接给出了 p-值,所以没有必要计算 t-统计值以及查 t 分布表。根据题意,如果 p- 值0,事实上其估 计值确是大于零的。同样地,随着人口的增加,住房需求也会随之增加,所以我们预期 β 4 >0, 事实上其估计值也是如此。随着房屋价格的上升,我们预期对住房的需求人数减少,即我们 预期 β 3估计值的符号为负,回归结果与直觉相符。出乎预料的是,地方税与州税为不显著 的。由于税收的增加将使可支配收入降低,所以我们预期住房的需求将下降。虽然模型 A 是这种情况,但它们的影响却非常微弱。 例 4、在经典线性模型基本假定下,对含有三个自变量的多元回归模型:

Y=B。+BX1+B2X2+E,X3+ 你想检验的虚拟假设是H。:阝-2阝2=1。 (1)用月,B2的方差及其协方差求出Var(B,-2B2)。 (2)写出检验H。:阝-2B2=1的t统计量。 (3)如果定义B-2B2=0,写出一个涉及B。、0、阝2和B3的回归方程,以便能直 接得到B估计值0及其标准误。 解答: (1)由数理统计学知识易知 Var(B-2B2)=Var(B)-4Cov(B .B)+4Var(B.) (2)由数理统计学知识易知 1=月-28,-1,其中5e房-20,)为(店-2月,)的标准差。 se(B1-2B2) (3)由阝,-2阝2=0知B1=0+2B2,代入原模型得 Y=B。+(0+2B2)X1+B2X2+F3X3+4 =B。+X1+B2(2X1+X2)+B3X3+4 这就是所需的模型,其中日估计值日及其标准误都能通过对该模型进行估计得到。 例5、对于涉及到三个变量Y、X,、X,的数据做以下回归: I Y:=do+aXu+u ⅡY,=B。+FX2+42 III Yi=Yo+Xu+r2X2i+3i 问在什么条件下才能有à1=氵,及B,=2,即多元回归与各自的一元回归所得的参数估计 值相同。 解答:由回归模型I与Ⅱ分别知: ∑xy
Y = β 0 + β1X1 + β 2 X 2 + β 3X3 + µ 你想检验的虚拟假设是 H0 : 2 1 β1 − β 2 = 。 (1)用 1 2 ˆ , β ˆ β 的方差及其协方差求出 ) ˆ 2 ˆ ( Var β1 − β 2 。 (2)写出检验 H0 : 2 1 β1 − β 2 = 的 t 统计量。 (3)如果定义 β1 − 2β 2 = θ ,写出一个涉及 β 0 、θ 、 β 2 和 β 3的回归方程,以便能直 接得到θ 估计值θ ˆ及其标准误。 解答: (1)由数理统计学知识易知 ) ˆ ) 4 ( ˆ , ˆ ) 4 ( ˆ ) ( ˆ 2 ˆ ( Var β1 − β 2 = Var β1 − Cov β1 β 2 + Var β 2 (2)由数理统计学知识易知 ) ˆ 2 ˆ ( 1 ˆ 2 ˆ 1 2 1 2 β β β β − − − = se t ,其中 ) ˆ 2 ˆ (β1 − β 2 se 为 ) ˆ 2 ˆ (β1 − β 2 的标准差。 (3)由 β1 − 2β 2 = θ 知 β1 = θ + 2β 2 ,代入原模型得 β θ β β µ β θ β β β µ = + + + + + = + + + + + 0 1 2 1 2 3 3 0 2 1 2 2 3 3 (2 ) ( 2 ) X X X X Y X X X 这就是所需的模型,其中θ 估计值θ ˆ及其标准误都能通过对该模型进行估计得到。 例 5、对于涉及到三个变量Y 、 X1、 X 2 的数据做以下回归: I Yi = α 0 +α1X1i + µ1i II Yi = β 0 + β1X 2i + µ 2i III Yi 0 1X1i 2 X 2i µ3i = γ + γ + γ + 问在什么条件下才能有 1 1 αˆ = γˆ 及 1 2 ˆ ˆ β = γ ,即多元回归与各自的一元回归所得的参数估计 值相同。 解答:由回归模型 I 与 II 分别知: ∑ ∑= 2 1 1 1 ˆ i i i x x y α , ∑ ∑= 2 2 2 1 ˆ i i i x x y β

对模型Ⅲ山,令其样本回归模型的离差形式为 yi=Y xui+y2x2i+e3i 求 ∑e=0y,-1-2x) 的最小值,可得如下正规方程组: ∑yxu=h∑x2+h2∑xx2 ∑yx=1∑x2+2∑x 解此方程组得 月=②)-y3x) ∑x∑-(∑xx) 分,-②)-y∑ ∑x∑x-(∑xx2)月 可见,当∑xx2,=0时,即X,与X2完全线性无关时(正交),有a=方及B,=乃2。由 此得多元回归的一个重要的结论:当各解释变量没有线性相关性时,多元回归中各解释变量 的参数等于分别进行一元回归时解释变量的参数。 三、教材练习题及其参考解答 1、多元线性回归模型的基本假设是什么?试说明在证明最小二乘估计量的无偏性和有 效性的过程中,哪些基本假设起了作用? 答:多元线性回归模型的基本假定仍然是针对随机误差项与针对解释变量两大类的假 设。针对随机误差项的假设有:零均值、同方差、无序列相关且服从正态分布:针对解释变 量的假设有:解释变量应具有非随机性,如果是随机的,则不能与随机误差项相关:各解释 变量之间不存在(完全)线性相关关系。 在证明最小二乘估计量的无偏性中,利用了解释变量非随机或与随机误差项不相关的假 定:在有效性的证明中,利用了随机误差项同方差且无序列相关的假定。 2、在多元线性回归分析中,t检验与F检验有何不同?在一元线性回归分析中二者是 否有等价的作用? 答:在多元线性回归分析中,t检验常被用作检验回归方程中各个参数的显著性,而F
对模型 III,令其样本回归模型的离差形式为 i i i i y x x e = 1 1 + 2 2 + 3 γ γ 求 2 1 1 2 2 2 ∑ = ( − − ) i i i i e y γ x γ x 的最小值,可得如下正规方程组: ∑ i i = ∑ i + ∑ i i y x x x x 2 1 2 2 1 1 1 γ γ ∑ = ∑ + ∑ 2 i 2i 1 1i 2i 2 2i y x γ x x γ x 解此方程组得 ∑ ∑ ∑ ∑ ∑ ∑ ∑ − − = 2 1 2 2 2 2 1 2 1 2 2 1 2 1 ( ) ( )( ) ( )( ) ˆ i i i i i i i i i i i x x x x y x x y x x x γ ∑ ∑ ∑ ∑ ∑ ∑ ∑ − − = 2 1 2 2 2 2 1 1 1 2 2 2 1 2 ( ) ( )( ) ( )( ) ˆ i i i i i i i i i i i x x x x y x x y x x x γ 可见,当∑ = 0 1i 2i x x 时,即 X1与 X 2 完全线性无关时(正交),有 1 1 αˆ = γˆ 及 1 2 ˆ ˆ β = γ 。由 此得多元回归的一个重要的结论:当各解释变量没有线性相关性时,多元回归中各解释变量 的参数等于分别进行一元回归时解释变量的参数。 三、教材练习题及其参考解答 1、多元线性回归模型的基本假设是什么?试说明在证明最小二乘估计量的无偏性和有 效性的过程中,哪些基本假设起了作用? 答:多元线性回归模型的基本假定仍然是针对随机误差项与针对解释变量两大类的假 设。针对随机误差项的假设有:零均值、同方差、无序列相关且服从正态分布;针对解释变 量的假设有:解释变量应具有非随机性,如果是随机的,则不能与随机误差项相关;各解释 变量之间不存在(完全)线性相关关系。 在证明最小二乘估计量的无偏性中,利用了解释变量非随机或与随机误差项不相关的假 定;在有效性的证明中,利用了随机误差项同方差且无序列相关的假定。 2、在多元线性回归分析中,t 检验与 F 检验有何不同?在一元线性回归分析中二者是 否有等价的作用? 答:在多元线性回归分析中,t 检验常被用作检验回归方程中各个参数的显著性,而 F

检验则被用作检验整个回归关系的显著性:各解释变量联合起来对被解释变量有显著的线性 关系,并不意味着每一个解释变量分别对被解释变量有显著的线性关系。在一元线性回归分 析中,二者具有等价作用,因为二者都是对共同的假设一一解释变量的参数等于零一一进行 检验。 3、为什么说对模型参数施加约束条件后,其回归的残差平方和一定不比未施加约束的残 差平方和小?在什么样的条件下,受约束回归与无约束回归的结果相同? 答:对模型参数施加约束条件后,就限制了参数的取值范围,寻找到的参数估计值也是 在此给条件下使残差平方和达到最小,它不可能比未施加约束条件时找到的参数估计值使得 残差平方达到的最小值还要小。但当约束条件为真时,受约束回归与无约束回归的结果就相 同了。 4、在一项调查大学生一学期平均成绩(Y)与每周在学习(X,)、睡觉(X,)、娱乐 (X,)与其他(X,)等各种活动所用时间的关系的研究中,建立如下回归模型: Y=Bo+BX+Bx2+Bx3+Bx+u 如果这些活动所用时间的总和为一周的总小时数168。问:保持其他变量不变,而改变其中 一个变量的说法是否有意义?该模型是否有违背基本假设的情况?如何修改此模型以使其 更加合理。 解答:由于X,+X,+X3+X4=168,当其中一个变量变化时,至少有一个其他变 量也得变化,因此,保持其他变量不变,而改变其中一个变量的说法是无意义的。 显然,由于四类活动的总和为一周的总小时数168,表明四个X间存在完全的线性关系, 因此违背了解释变量间不存在(完全)多重共线性的假设。 可以去掉其中的一个变量,如去掉代表“其他”活动的变量X,则新构成的三变量模 型更加合理。如这时B就测度了当其他两变量不变时,每周增加1小时的学习时间所带来 的学习成绩的平均变化。这时,即使睡觉和娱乐的时间保持不变,也可以通过减少其他活动 的时间来增加学习的时间。而这时三个变量间也不存在明显的共线性问题。 5、考虑下列两个模型: I Y=ao+aXu+a2X2i+u Yi-Xi=Bo+BX+B2x2+v
检验则被用作检验整个回归关系的显著性;各解释变量联合起来对被解释变量有显著的线性 关系,并不意味着每一个解释变量分别对被解释变量有显著的线性关系。在一元线性回归分 析中,二者具有等价作用,因为二者都是对共同的假设——解释变量的参数等于零——进行 检验。 3、为什么说对模型参数施加约束条件后,其回归的残差平方和一定不比未施加约束的残 差平方和小?在什么样的条件下,受约束回归与无约束回归的结果相同? 答:对模型参数施加约束条件后,就限制了参数的取值范围,寻找到的参数估计值也是 在此给条件下使残差平方和达到最小,它不可能比未施加约束条件时找到的参数估计值使得 残差平方达到的最小值还要小。但当约束条件为真时,受约束回归与无约束回归的结果就相 同了。 4、在一项调查大学生一学期平均成绩(Y )与每周在学习( X1)、睡觉( X 2 )、娱乐 ( X3)与其他( X 4 )等各种活动所用时间的关系的研究中,建立如下回归模型: Y = β 0 + β1X1 + β 2 X 2 + β 3X3 + β 4 X 4 + µ 如果这些活动所用时间的总和为一周的总小时数 168。问:保持其他变量不变,而改变其中 一个变量的说法是否有意义?该模型是否有违背基本假设的情况?如何修改此模型以使其 更加合理。 解答:由于 X1 + X 2 + X3 + X 4 = 168 ,当其中一个变量变化时,至少有一个其他变 量也得变化,因此,保持其他变量不变,而改变其中一个变量的说法是无意义的。 显然,由于四类活动的总和为一周的总小时数 168,表明四个 X 间存在完全的线性关系, 因此违背了解释变量间不存在(完全)多重共线性的假设。 可以去掉其中的一个变量,如去掉代表“其他”活动的变量 X 4 ,则新构成的三变量模 型更加合理。如这时 β1就测度了当其他两变量不变时,每周增加 1 小时的学习时间所带来 的学习成绩的平均变化。这时,即使睡觉和娱乐的时间保持不变,也可以通过减少其他活动 的时间来增加学习的时间。而这时三个变量间也不存在明显的共线性问题。 5、考虑下列两个模型: I Yi = α 0 +α1X1i +α 2 X 2i + ui II i i i i i Y − X = + X + X + v 1 β 0 β1 1 β 2 2

(1)证明:月=a1-1,B。=ao,B2=a2。 (2)证明:两个模型的最小二乘残差相等,即对任何i,有ⅱ=,。 (3)在什么条件下,模型Ⅱ的R小于模型I的R2? 解答:(1)对模型Ⅱ变形如下: Y=B。+(B+1)X,+B2X2+ 因此,在与模型I有相同的样本下进行OLS估计,有 a1=月1+1,B。=ao,B2=a2 或 B=a,-l,B。=a,B2=a2 (2)在(1)成立的条件下, i,=Y,-a。-aXu-d2X2 -Y,-B。-(B1+1)X-B2X2 =I,-X-B。-BXu-B2X= (3)对模型I,R2=1 ∑好 ∑Y,-) 对模型Ⅱ,R2=1 ∑好 ∑心,-X)-(夜-x2 由(2)知∑立,=∑,故,只有当∑[(化,-X)-(了-x<∑(化,-)2时, 即模型Ⅱ的总变差(解释变量的离差平方和)小于模型1的总变差(解释变量的离差平方 和)时,才会有模型Ⅱ的R小于模型I的R2。 6、考虑下列三个试验步骤 (1)对Y,=B。+BX,+B2X2+4,进行回归 (2)对X:=+aX2+y,进行回归,计算残差 (3)对Y,=Y。+Y,+Y2X2+w,进行回归 试证明B,=分1,并直观地解释该结果。 证明:由(2)计算残差,:=X:-C。-aX2,代入到(3)的回归中得:
(1)证明: ˆ 1 ˆ β1 = α1 − , 0 0 ˆ β ˆ = α , 2 2 ˆ β ˆ = α 。 (2)证明:两个模型的最小二乘残差相等,即对任何i ,有 i i uˆ = vˆ 。 (3)在什么条件下,模型 II 的 2 R 小于模型 I 的 2 R ? 解答:(1)对模型 II 变形如下: i i i i Y = + + X + X + v 0 1 1 2 2 β (β 1) β 因此,在与模型 I 有相同的样本下进行 OLS 估计,有 1 ˆ ˆα1 = β1 + , 0 0 ˆ β ˆ = α , 2 2 ˆ β ˆ = α 或 ˆ 1 ˆ β1 = α1 − , 0 0 ˆ β ˆ = α , 2 2 ˆ β ˆ = α (2)在(1)成立的条件下, i i i i i i i i i i i i Y X X X v Y X X u Y X X ˆ ˆ ˆ ˆ ˆ 1) ˆ ( ˆ ˆ ˆ ˆ ˆ 1 0 1 1 2 2 0 1 1 2 2 0 1 1 2 2 = − − − − = = − − + − = − − − β β β β β β α α α (3)对模型 I, ∑ ∑ − = − 2 2 2 ( ) ˆ 1 Y Y u R i i 对模型 II, ∑ ∑ − − − = − 2 2 2 2 2 [( ) ( )] ˆ 1 Y X Y X v R i i i 由(2)知∑ i = ∑ i uˆ vˆ ,故,只有当∑ − − − < ∑ − 2 2 2 2 [(Y X ) (Y X )] (Y Y ) i i i 时, 即模型 II 的总变差(解释变量的离差平方和)小于模型 1 的总变差(解释变量的离差平方 和)时,才会有模型 II 的 2 R 小于模型 I 的 2 R 。 6、考虑下列三个试验步骤 (1)对Yi = β 0 + β1X1i + β 2 X 2i + ui 进行回归 (2)对 i i i X = + X + v 1 α 0 α1 2 进行回归,计算残差 i vˆ (3)对 i i X i wi Y = γ 0 + γ 1vˆ + γ 2 2 + 进行回归 试证明 1 1ˆ ˆ β = γ ,并直观地解释该结果。 证明:由(2)计算残差 i vˆ : i X i X i v 1 0 1 2 ˆ = −αˆ −αˆ ,代入到(3)的回归中得:

Yi=Yo+(Xli-ao-ax2i)+Y2X2i+Wi Y=(ro-dor)+Xu+(Y2-a)X2i+w 可见,模型形式与步骤(1)中的完全相同,因此必有B,=1。直观地看,”,测度的是X2 以外的因素对X,的影响。因此对(3)中的模型来说,,对Y的影响只能归结到X,对Y的 影响上来,与X2无关。所以,(1)中模型的B与(3)中模型的y1都是测度排除了X2后 的X,对Y的影响,二者的回归结果应是相等的。 7、考虑以下过原点回归 Y=B Xu+B2x2+e (1)求参数的OLS估计量: (2)对该模型,是否仍有结论∑e,=0,∑e,X,=0,∑e,X,=0。 解:(1)根据最小二乘原理,需求适当的B、B,使得残差平方和最小: Mim∑e=∑(g,-BXu-B2,X2)2 由微积分的知识,对上式分别关于户、户2求偏导,并令导数值为零得如下正规方程组: ∑化-B.X,-B2,X2)Xu=0 ∑,-BX-BX2x)Xx=0 或 B∑X7+B2∑X,X=∑X,Y B∑XX+B2∑X经=∑XY 解得 A=②Yx②X)-②yX2x,K) ∑X∑X2-(∑XX)月 A=②Yx)-②y,X2x,x) ∑X∑X-(∑X,X)月 (2)由(1)中的正规方程组知,对该模型,仍有
Yi = 0 + 1 X1i − 0 − 1X 2i + 2 X 2i + wi γ γ ( αˆ αˆ ) γ 或 Yi = 0 − 0 1 + 1X1i + 2 − 1 1 X 2i + wi (γ αˆ γ ) γ (γ αˆ γ ) 可见,模型形式与步骤(1)中的完全相同,因此必有 1 1ˆ ˆ β = γ 。直观地看, i v 测度的是 X 2 以外的因素对 X1的影响。因此对(3)中的模型来说, i vˆ 对Y 的影响只能归结到 X1对Y 的 影响上来,与 X 2 无关。所以,(1)中模型的 β1与(3)中模型的 1 γ 都是测度排除了 X 2 后 的 X1对Y 的影响,二者的回归结果应是相等的。 7、考虑以下过原点回归 i i i i Y = X + X + e 1 1 2 2 β ˆ β ˆ (1)求参数的 OLS 估计量; (2)对该模型,是否仍有结论∑ = 0 i e , ∑ = 0 i X1i e , ∑ = 0 i X 2i e 。 解:(1)根据最小二乘原理,需求适当的 1 ˆ β 、 2 ˆ β ,使得残差平方和最小: Min ∑ = ∑ − − 2 1 1 2 2 2 ) ˆ ˆ ( i Yi X i i X i e β β 由微积分的知识,对上式分别关于 1 β ˆ 、 2 ˆ β 求偏导,并令导数值为零得如下正规方程组: ∑ − − ) = 0 ˆ ˆ (Yi β1i X1i β 2i X 2i X1i ∑ − − ) = 0 ˆ ˆ (Yi β1i X1i β 2i X 2i X 2i 或 ∑X i + 2∑X1i X 2i = ∑X1i Yi 2 1 1 β ˆ β ˆ ∑X i X i + ∑X i = ∑X 2i Yi 2 1 1 2 2 2 β ˆ β ˆ 解得 ∑ ∑ ∑ ∑ ∑ ∑ ∑ − − = 2 1 2 2 2 2 1 2 1 2 2 1 2 1 ( ) ( )( ) ( )( ) ˆ i i i i i i i i i i i X X X X Y X X Y X X X β ∑ ∑ ∑ ∑ ∑ ∑ ∑ − − = 2 1 2 2 2 2 1 1 1 2 2 2 1 2 ( ) ( )( ) ( )( ) ˆ i i i i i i i i i i i X X X X Y X X Y X X X β (2)由(1)中的正规方程组知,对该模型,仍有

∑e,X,=0 ∑e,Xx=0 但不存在∑,=0。即过原点的残差和不一定为零。 8、对多元线性回归模型Y=X邱+μ,试证明随机误差项4的方差的无偏估计量为 62= e'e 。其中e为相应样本回归模型的残差向量。 n-k-1 证: 由于被解释变量的估计值与观测值之间的残差 e=Y-X邛 =Xβ+μ-X(XX)-X'(XB+μ) =μ-X(XX)-X'μ =(I-X(X'X)X =Mμ 残差的平方和为: e'e=μ'M'Mμ 因为M=(I-X(XX)1X)为对称等幂矩阵,即 M=M' M2=M'M=M 所以有 e'e=μ'Mμ E(e'e)=Eμ'I-X(XX)-X)μ) =σ2tr(I-X(XX)-X') =σ2(trl-tr(X(XX)X') =o2(n-(k+1) 其中符号“”表示矩阵的迹,其定义为矩阵主对角线元素的和。于是 02= E(e'e) n-k-1 以上过程既导出了随机误差项方差的估计量为 2=e'e n-k-1 也证明了该估计量是无偏估计量。 9、对多元线性回归模型Y=X邓+μ,试证明普通最小二乘估计量B具有最小方差性。 证:
∑ = 0 i X1i e ∑ = 0 i X 2i e 但不存在∑ = 0 i e 。即过原点的残差和不一定为零。 8、对多元线性回归模型 Y = Xβ + μ ,试证明随机误差项 µ 的方差的无偏估计量为 1 ˆ 2 − − ′ = n k e e σ 。其中e 为相应样本回归模型的残差向量。 证: 由于被解释变量的估计值与观测值之间的残差 e = Y − Xβˆ Mμ I X X X X μ μ X X X X μ Xβ μ X X X X Xβ μ = = − ′ ′ = − ′ ′ = + − ′ ′ + − − − ( ( ) ) ( ) ( ) ( ) 1 1 1 残差的平方和为: e′e =μ ′M′Mμ 因为 ( ( ) ) 1 M = I − X X′X X′ − 为对称等幂矩阵,即 M M M M M M = ′ = ′ = 2 所以有 e′e = μ ′Mμ ( ( 1)) ( ( ( ) )) ( ( ) ) ( ) ( ( ( ) ) ) 2 2 1 2 1 1 = − + = − ′ ′ = − ′ ′ ′ = ′ − ′ ′ − − − n k tr tr tr E E σ σ σ I X X X X I X X X X e e μ I X X X X μ 其中符号“tr”表示矩阵的迹,其定义为矩阵主对角线元素的和。于是 1 ( ) 2 − − ′ = n k E e e σ 以上过程既导出了随机误差项方差的估计量为 1 ˆ 2 − − ′ = n k e e σ 也证明了该估计量是无偏估计量。 9、对多元线性回归模型Y = Xβ + μ ,试证明普通最小二乘估计量βˆ 具有最小方差性。 证: