
Investment Science Part Il:Single-Period Random Cash Flows Dr.Xi CHEN Department of Management Science and Engineering International Business School Beijing Foreign Studies University 100089,Beijing,People's Republic of China 4口,40+4立4至,三)及0 Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 1/81
Investment Science Part II: Single-Period Random Cash Flows Dr. Xi CHEN Department of Management Science and Engineering International Business School Beijing Foreign Studies University 100089, Beijing, People’s Republic of China Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 1 / 81

Asset Return Outline ①Asset Return Random Variables(self-learning) Random Returns (self-learning) Portfolio Mean and Variance The Feasible Set ⑥The Markowitz Model The Two-Fund Theorem Inclusion of a Risk-Free Asset The One-Fund Theorem 4口40+4三4至,至)只0 Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 3/81
Asset Return Outline 1 Asset Return 2 Random Variables (self-learning) 3 Random Returns (self-learning) 4 Portfolio Mean and Variance 5 The Feasible Set 6 The Markowitz Model 7 The Two-Fund Theorem 8 Inclusion of a Risk-Free Asset 9 The One-Fund Theorem Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 3 / 81

Asset Return An investment instrument that can be bought and sold is frequently called an asset. o Suppose that you purchase an asset at time zero,and 1 year later you sell the asset.The total return on your investment is defined to be amount received total return X amount invested or R=X For simplicity,the term return is used for total return. o The rate of return is rate of return amount received-amount invested amount invested I= X1-Xo Xo =R-1. The shorter expression return is also frequently used for the rate of return. )Q0 Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 4/81
Asset Return An investment instrument that can be bought and sold is frequently called an asset. Suppose that you purchase an asset at time zero, and 1 year later you sell the asset. The total return on your investment is defined to be total return = amount received amount invested or R = X1 X0 . For simplicity, the term return is used for total return. The rate of return is rate of return = amount received - amount invested amount invested r = X1 − X0 X0 = R − 1. The shorter expression return is also frequently used for the rate of return. Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 4 / 81

Asset Return Short Sales Sometimes it is possible to sell an asset that you do not own through the process of short selling,or shorting,the asset. o Short selling is considered quite risky-even dangerous-by many investors. o When short selling a stock,you are essentially duplicating the role of the issuing corporation.You sell the stock to raise immediate capital. If the stock pays dividends during the period that you have borrowed it,you too must pay that same dividend to the person from whom you borrowed the stock. o We receive Xo initially and pay X1 later,so the outlay is-Xo and the final receipt is-X1,and hence R=-X今-X=-X%R=-X(1+) -X0 Therefore,the return value R applies algebraically to both purchases and short sales. Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 5/81
Asset Return Short Sales Sometimes it is possible to sell an asset that you do not own through the process of short selling, or shorting, the asset. Short selling is considered quite risky-even dangerous-by many investors. When short selling a stock, you are essentially duplicating the role of the issuing corporation. You sell the stock to raise immediate capital. If the stock pays dividends during the period that you have borrowed it, you too must pay that same dividend to the person from whom you borrowed the stock. We receive X0 initially and pay X1 later, so the outlay is −X0 and the final receipt is −X1, and hence R = −X1 −X0 ⇒ −X1 = −X0R = −X0(1 + r). Therefore, the return value R applies algebraically to both purchases and short sales. Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 5 / 81

Asset Return Example (A short sale) Suppose I decide to short 100 shares of stock in company CBA.This stock is currently selling for $10 per share.I borrow 100 shares from my broker and sell these in the stock market,receiving $1,000.At the end of 1 year the price of CBA has dropped to $9 per share.I buy back 100 shares for $900 and give these shares to my broker to repay the original loan. Because the stock price fell,this has been a favorable transaction for me.I made a profit of $100. Someone who purchased the stock at the beginning of the year and sold it at the end would have lost $100,with R=0.9 or r=-0.1. The rate of return is clearly negative as r=-0.1.Shorting converts a negative rate of return into a profit because the original investment is also negative.For my shorting activity on CBA my original outlay was-51,000; hence my profit is-$1,000 x r=$100. Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 6/81
Asset Return Example (A short sale) Suppose I decide to short 100 shares of stock in company CBA. This stock is currently selling for $10 per share. I borrow 100 shares from my broker and sell these in the stock market, receiving $1,000. At the end of 1 year the price of CBA has dropped to $9 per share. I buy back 100 shares for $900 and give these shares to my broker to repay the original loan. Because the stock price fell, this has been a favorable transaction for me. I made a profit of $100. Someone who purchased the stock at the beginning of the year and sold it at the end would have lost $100, with R = 0.9 or r = −0.1. The rate of return is clearly negative as r = −0.1. Shorting converts a negative rate of return into a profit because the original investment is also negative. For my shorting activity on CBA my original outlay was -$1,000; hence my profit is −$1, 000 × r = $100. Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 6 / 81

Asset Return Portfolio Return Suppose now that n different assets are available.We can form a master asset,or portfolio,of these n assets. Suppose that this is done by apportioning a total amount Xo among the n assets.We then select amounts Xoi,i=1,2,...,n,such that 1oi=Xo.where Xoi represents the amount invested in the ith asset. If we are allowed to sell an asset short,then some of the Xoi's can be negative;otherwise we restrict the Xoi's to be nonnegative. The amounts invested can be expressed as fractions of Xo,i.e., Xoi wiXo,i=1,2,...,n, ∑%=1, i=1 where wi is the weight or fraction of asset i in the portfolio. )Q0 Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 7/81
Asset Return Portfolio Return Suppose now that n different assets are available. We can form a master asset, or portfolio, of these n assets. Suppose that this is done by apportioning a total amount X0 among the n assets. We then select amounts X0i P , i = 1, 2, . . . , n, such that n i=1 X0i = X0, where X0i represents the amount invested in the ith asset. If we are allowed to sell an asset short, then some of the X0i ’s can be negative; otherwise we restrict the X0i ’s to be nonnegative. The amounts invested can be expressed as fractions of X0, i.e., X0i = wiX0, i = 1, 2, . . . , n, Xn i=1 wi = 1, where wi is the weight or fraction of asset i in the portfolio. Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 7 / 81

Asset Return Let R;denote the total return of asset i.We have R=无2Rw必=2R1+1-1+月 i=1 Formula(Portfolio return) Both total return and the rate of return of a portfolio of assets are equal to the weighted sum of the corresponding individual asset returns,with the weight of an asset being its relative weight(in purchase cost)in the portfolio;that is, R=∑R,=∑ =1 i=1 Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 8/81
Asset Return Let Ri denote the total return of asset i. We have R = 1 X0 Xn i=1 RiwiX0 = Xn i=1 wiRi ⇒ 1 + r = Xn i=1 wi(1 + ri) ⇒ r = Xn i=1 wiri . Formula (Portfolio return) Both total return and the rate of return of a portfolio of assets are equal to the weighted sum of the corresponding individual asset returns, with the weight of an asset being its relative weight (in purchase cost) in the portfolio; that is, R = Xn i=1 wiRi , r = Xn i=1 wiri . Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 8 / 81
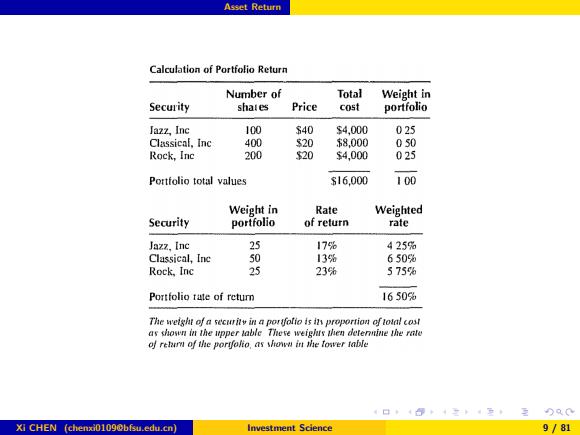
Asset Return Calculation of Portfolio Return Number of Total Weight in Security shales Price cost portfolio Jazz,Inc 100 340 s4,000 025 Classical,Inc 400 $20 $8,000 0s0 Rock,Inc 200 20 s4,000 025 Portfolio total values 316.000 100 Weight in Rate Weighted Security portfolio of return rate Jazz,【nc 25 17% 425% Classical,Inc 50 13% 650% Rock,Inc 25 23% 575% Portfolio tate of retum 1650% The weight of a securits in a poryfolio is in proportion of total cost as shown in the upper lable Theve weighus then deternine the rate of retarn of the porgfolio,as showu in the Tower table Xi CHEN (chenxi01090bfsu.edu.cn) Investment Science 9/81
Asset Return Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 9 / 81

Random Variables (self-learning) Outline 19 Asset Return ② Random Variables (self-learning) Random Returns (self-learning) Portfolio Mean and Variance The Feasible Set ⑥The Markowitz Model The Two-Fund Theorem Inclusion of a Risk-Free Asset The One-Fund Theorem 4口4+4三4至,至)只0 Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 10/81
Random Variables (self-learning) Outline 1 Asset Return 2 Random Variables (self-learning) 3 Random Returns (self-learning) 4 Portfolio Mean and Variance 5 The Feasible Set 6 The Markowitz Model 7 The Two-Fund Theorem 8 Inclusion of a Risk-Free Asset 9 The One-Fund Theorem Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 10 / 81

Random Returns (self-learning) Outline Asset Return Random Variables (self-learning) 3 Random Returns(self-learning) Portfolio Mean and Variance The Feasible Set ⑥The Markowitz Model The Two-Fund Theorem Inclusion of a Risk-Free Asset The One-Fund Theorem 4口4+4三4至,至)只0 Xi CHEN (chenxi01090bfsu.edu.cn) Investment Science 11/81
Random Returns (self-learning) Outline 1 Asset Return 2 Random Variables (self-learning) 3 Random Returns (self-learning) 4 Portfolio Mean and Variance 5 The Feasible Set 6 The Markowitz Model 7 The Two-Fund Theorem 8 Inclusion of a Risk-Free Asset 9 The One-Fund Theorem Xi CHEN (chenxi0109@bfsu.edu.cn) Investment Science 11 / 81