
复习上节课 s=n hv n=为整数。1hv,2hv,3hv 1900年Planck假定: 黑体中的原子分子辐射能量时作简谐振动,它只能发射或吸收频率为ⅴ,数 值为ε=hv的整数倍电磁能,n=为整数。1hv,2hv,3hv 结论:能量量子化
1900年Planck假定: 黑体中的原子分子辐射能量时作简谐振动,它只能发射或吸收频率为ν ,数 值为=hν的整数倍电磁能, n =为整数。 1hν,2hν,3hν = n hν n =为整数。 1hν,2hν,3hν 结论:能量量子化 复习上节课

Ax△px≥h 不确定关系或称不确定原理 适用于电子等微观粒子 不确定关系表明:对于微观粒子不能同 时用确定的位置和确定的动量来描述。 2
2 xpx h 不确定关系表明:对于微观粒子不能同 时用确定的位置和确定的动量来描述。 不确定关系或称不确定原理 适用于电子等微观粒子
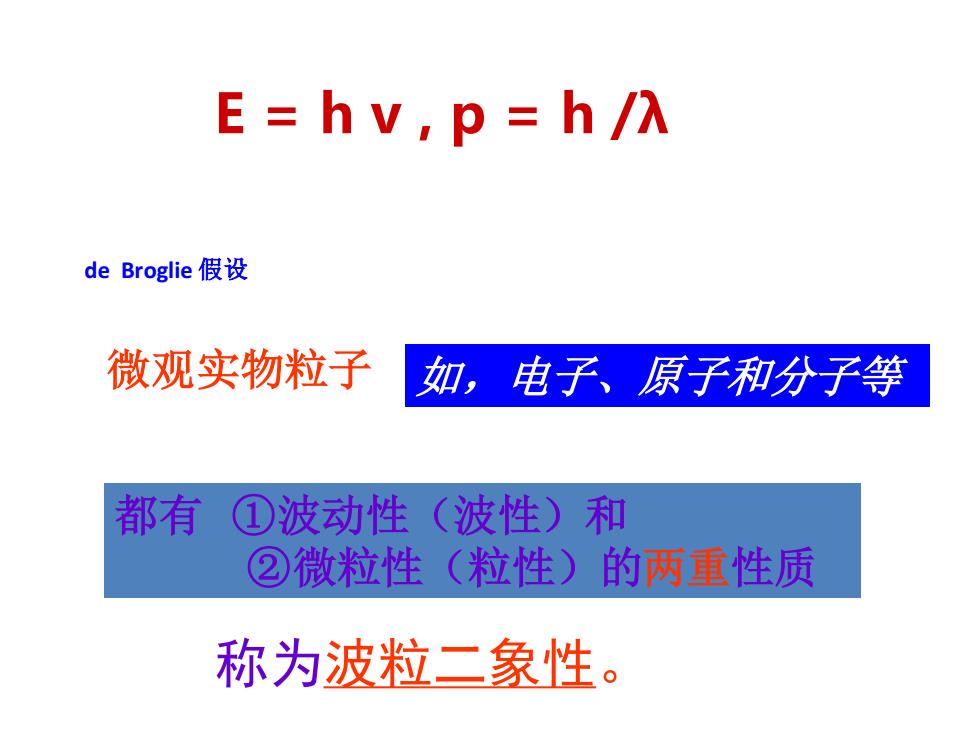
E=hv,p h/A de Broglie假设 微观实物粒子 如,电子、原子和分子等 都有 ①波动性(波性)和 ②微粒性(粒性)的两重性质 称为波粒二象性
E = h v , p = h /λ 称为波粒二象性。 de Broglie 假设 微观实物粒子 如,电子、原子和分子等 都有 ①波动性(波性)和 ②微粒性(粒性)的两重性质

复习上节课 假设3:若某一力学量A的算符[A]作用于某一 状态函数ψ后,等于某一常数a乘以ψ,即 [A]=aΨ 那么对ψ所描述的这个微观体系的状态,其力 学量A具有确定的数值a, a称为力学量算符[A]的本征值, Ψ称为A的本征态或本征波函数, 上式称为A的本征方程
复习上节课 假设3:若某一力学量 A 的算符[A] 作用于某一 状态函数ψ后,等于某一常数 a 乘以ψ,即 [A]ψ= aψ 那么对ψ所描述的这个微观体系的状态,其力 学量 A 具有确定的数值a, a 称为力学量算符 [A] 的本征值, ψ 称为A的本征态或本征波函数, 上式称为A的本征方程
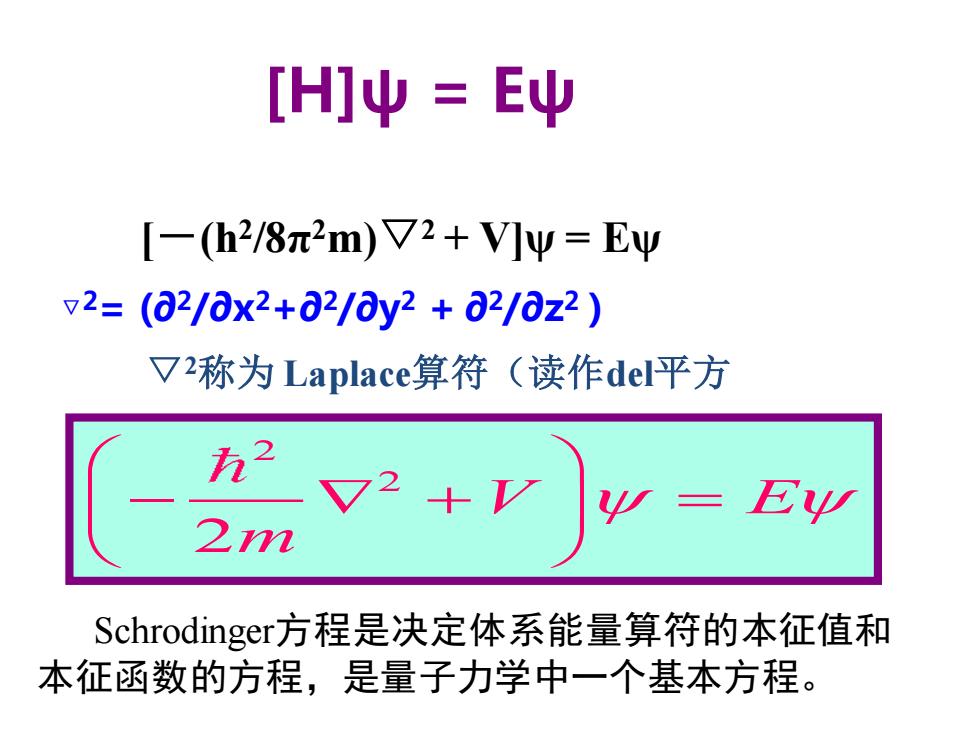
[H]ψ=EΨ [-(h2/8π2m)V2+V]小Ψ=EΨ v2=(a2/ax2+∂2/ay2+a2/az2) V2称为Laplace算符(读作del平方 EΨ Schrodinger方程是决定体系能量算符的本征值和 本征函数的方程,是量子力学中一个基本方程
[-(h2 /8π 2m)▽2 + V]ψ = Eψ [H]ψ = Eψ ▽2= (∂2/∂x 2+∂2/∂y 2 + ∂2/∂z 2 ) ▽2称为 Laplace算符(读作del平方 2 2 2 V E m − + = Schrodinger方程是决定体系能量算符的本征值和 本征函数的方程,是量子力学中一个基本方程

第一章量子力学基础 1.3箱中粒子的Schrodinger方程及其解 v-Ev h2 2m 作者:Abliz Yimit 1
1 第一章量子力学基础 1.3 箱中粒子的 Schrodinger 方程及其解 作者:Abliz Yimit 2 2 2 V E m − + =

第一章量子力学基础 1.3箱中粒子的Schrodinger方程及其解 ①/=01y=0.四y=0 一维势箱中粒子是指: 一个质量为的粒子被置于箱 外势能无穷大、箱内势能为零 (即无限深)的箱中,沿方向 某运婪际问愿,例如金属内的自 ψΨ≠0 由电子或共轭分子的π电子等, ψ=0 Ψ=0 可以作为一种近似,采用势箱 中的粒子模型来处理 0 1 2
第一章量子力学基础 1.3 箱中粒子的 Schrodinger 方程及其解 一维势箱中粒子是指: 一个质量为m的粒子被置于箱 外势能无穷大、箱内势能为零 (即无限深)的箱中,沿x方向 运动. 可以作为一种近似,采用势箱 中的粒子模型来处理 某些实际问题,例如金属内的自 由电子或共轭分子的π电子等, ψ=0 ψ=0 ψ≠0 2

第一章量子力学基础 1.3箱中粒子的Schrodinger方程及其解 0 0<x<l W=o■Iy=0y=o V(x)= x≤0或x≥1 该粒子在箱外永不出现,可以直接写出其零解:只 ψ≠0 有在箱内才需要建立Schr心dinger方程并求解: =0 Ψ=0 由于势箱内V=0,因此箱内的薛定谔方程为: 盆总Ew (其中h=知)》 其通解为: +c2 sin √2mE 3
第一章量子力学基础 1.3 箱中粒子的 Schrodinger 方程及其解 该粒子在箱外永不出现,可以直接写出其零解; 只 有在箱内才需要建立Schrödinger方程并求解: V(x)= 0 0 x l x 0或x l 由于势箱内V=0,因此箱内的薛定谔方程为: (x) E (x) dx d m − 2 = 2 2 2 ( ) 2 h 其中 = 其通解为: ψ=0 ψ=0 ψ≠0 3

第一章量子力学基础 1.3箱中粒子的Schrodinger方程及其解 根据品优波函数的连续性和单值条件, 当x=0和x=1时,ψ=0 即x=0时w(0)=c1cos(0)+c2sin(0)=0 则:c1=0 cl X1+c2 X0=0 x=l时ΨI)=C2sin(8π2mE/h2)2I=0 C2不能为0 故必须是:(8π2mE/h2)2l=n元n=1,2,3,. n≠0 子12 812 Ψ(k)=c2sin(nπx/l)=(2n)2sin(nx/l) 归一化条件求: C2=(2L)2
第一章量子力学基础 1.3 箱中粒子的 Schrodinger 方程及其解 x = l 时 Ψ(l)= c2 sin (8π 2m E / h2 ) 1/2 l = 0 c2不能为 0 故必须是: (8π 2m E / h2 ) 1/2 l = n π n =1,2,3,. n≠ 0 ∴ Ψ(x)= c2 sin (n πx / l )=(2/l )1/2 sin (n πx / l ) 归一化条件求: c2 =(2/l )1/2 根据品优波函数的连续性和单值条件, 当x = 0 和 x = l 时, ψ= 0 即 x = 0 时 ψ(0)= c1cos (0) + c2 sin (0)= 0 则:c1 = 0 c1 ×1+ c2 ×0= 0 4

第一章量子力学基础 1.3箱中粒子的Schrodinger方程及其解 然后用归一化法定出C2 bv"wix-1 2记 令 0 =c2-m2=5-0 2汇 四 =1 2 Sif 5
然后用归一化法定出 令 第一章量子力学基础 1.3 箱中粒子的 Schrodinger 方程及其解 5