
5.5 离域键和共轭效应 5.5.1离域π键的形成和表示法 (一)一般兀键 例如乙烯分子C2H4,每个C原子价轨道作sp杂化, 与另一个C原子和两个H原子形成三个σ键, 还有一个p轨道与另一个C原子的 p轨道重叠,形成双原子的π键。 乙烯分子属于D2对称点群
(一)一般π键 例如乙烯分子C2H4,每个C原子价轨道作sp2杂化, 与另一个C原子和两个H原子形成三个σ键, 5.5.1 离域π键的形成和表示法 1 + - C C 还有一个p轨道与另一个C原子的 p轨道重叠,形成双原子的π键。 乙烯分子属于D2h对称点群

第五章Huckel分子轨道法 (二)离域π键的形成和表示法 形成π键的电子不局限于两个原子的区域,而是在参加成键 的多个原子形成的分子骨架中运动,这种化学键称为离域π键。 在经典结构式中,由单键和双键交替连结的这些原子,通常 能够形成多原子π键,又称离域键。 一般地说,满足下面两个条件就可以形成离域T键: ()原子共面,每个原子可提供一个方向相同的轨道; (②)π电子数少于参加成键的p轨道数的2倍。 ?? 但是要注意,这两个条件并不是绝对的,常常还要由分子 的性质进行判断。 2
(二)离域π键的形成和表示法 形成π键的电子不局限于两个原子的区域,而是在参加成键 的多个原子形成的分子骨架中运动,这种化学键称为离域 π 键。 在经典结构式中,由单键和双键交替连结的这些原子,通常 能够形成多原子π键,又称离域π键。 一般地说,满足下面两个条件就可以形成离域π键: ⑴ 原子共面,每个原子可提供一个方向相同的p轨道; 但是要注意,这两个条件并不是绝对的,常常还要由分子 的性质进行判断。 ⑵ π电子数少于参加成键的p轨道数的2倍。 ??? 第五章 Huckel 分子轨道法 2

第五章Huckel分子轨道法 离域π键可用门m。表示,下标n为参加成键的原子 数目,上标m为电子数。 含有离域π键的分子,常常又称为共轭分子。 共轭分子的结构可用分子的结构式中将参加形成离 域π键的原子间用虚线连接,再将各个原子提供的电 子用黑点表示。 N=N0 3
离域π键可用 Πm n 表示,下标n为参加成键的原子 数目,上标m为电子数。 第五章 Huckel 分子轨道法 含有离域π键的分子,常常又称为共轭分子。 共轭分子的结构可用分子的结构式中将参加形成离 域π键的原子间用虚线连接,再将各个原子提供的电 子用黑点表示。 3 N N O . . . . .

第五章Huckel分子轨道法 共振结构式 也可以用两个或多个价 键共振结构式表达,把分子 的真实结构看作由这些价键 结构的共振式叠加的结果。 4
第五章 Huckel 分子轨道法 共振结构式 4 也可以用两个或多个价 键共振结构式表达,把分子 的真实结构看作由这些价键 结构的共振式叠加的结果
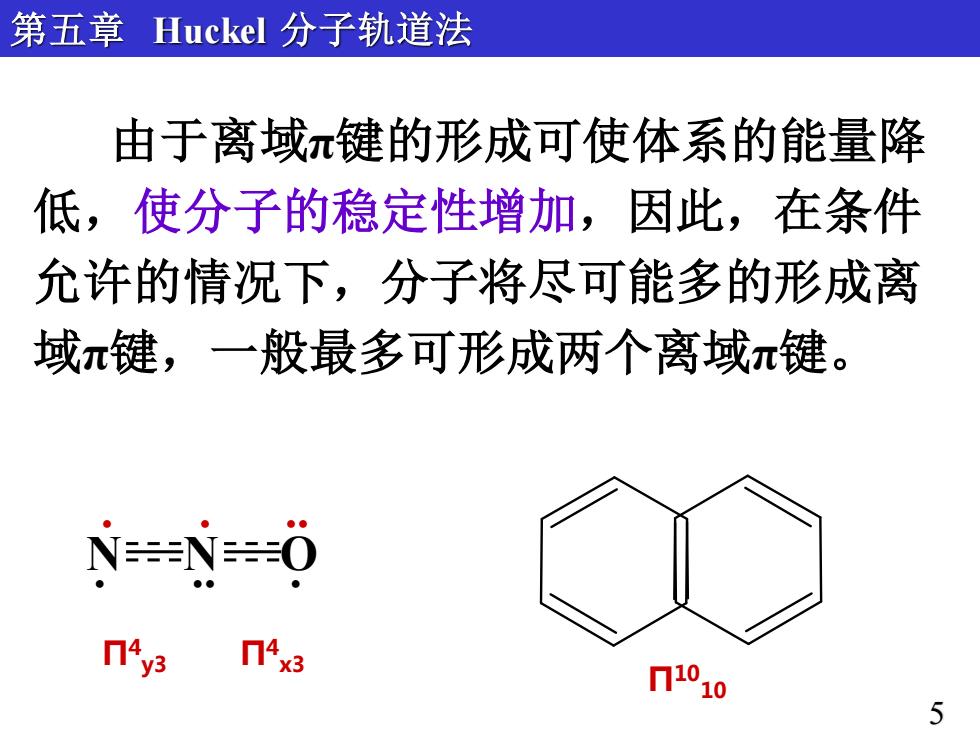
第五章Huckel分子轨道法 由于离域π键的形成可使体系的能量降 低,使分子的稳定性增加,因此,在条件 允许的情况下,分子将尽可能多的形成离 域π键,一般最多可形成两个离域π键。 NN0 Π4y3 n4x3 71010 5
由于离域π键的形成可使体系的能量降 低,使分子的稳定性增加,因此,在条件 允许的情况下,分子将尽可能多的形成离 域π键,一般最多可形成两个离域π键。 第五章 Huckel 分子轨道法 Π10 10 5 Π4 y3 Π4 x3 N N O . . . . .
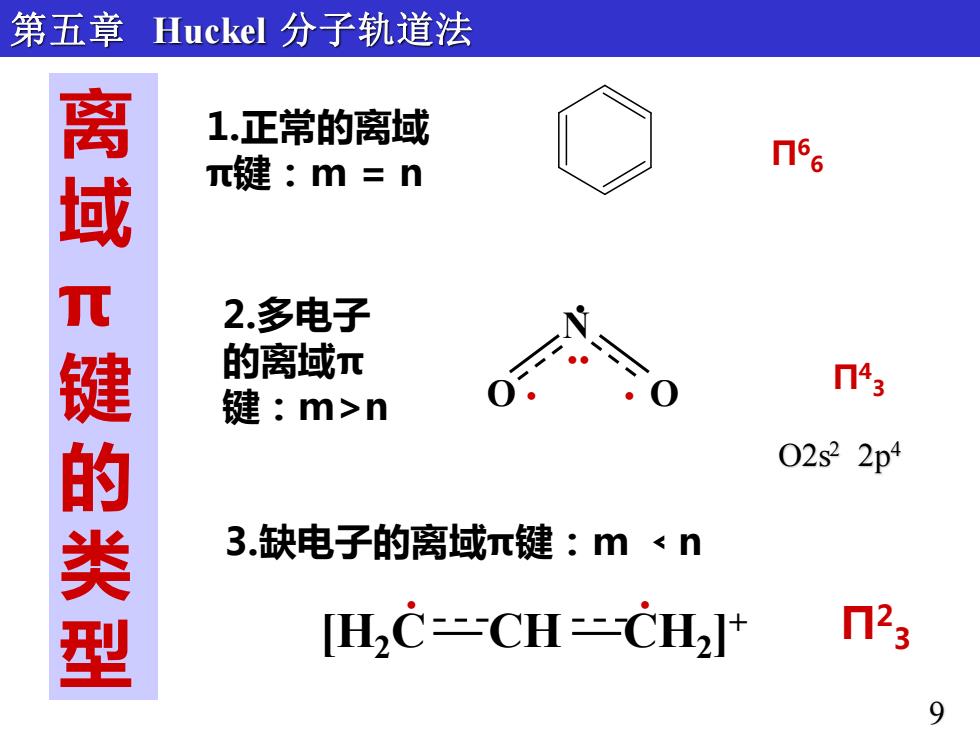
第五章 Huckel分子轨道法 离 1.正常的离域 π键:m=n n66 键的类型 2.多电子 的离域π 门43 键:m>n 02s2 3.缺电子的离域π键:m<n [HC-CH-CH2]i n23 9
离 域 π 键 的 类 型 Π6 6 1.正常的离域 π键:m = n 2.多电子 的离域π 键:m>n 3.缺电子的离域π键:m ﹤n Π2 [H 3 2C CH CH2 ] + . . Π4 3 . . . N O O . 第五章 Huckel 分子轨道法 9 O2s2 2p4
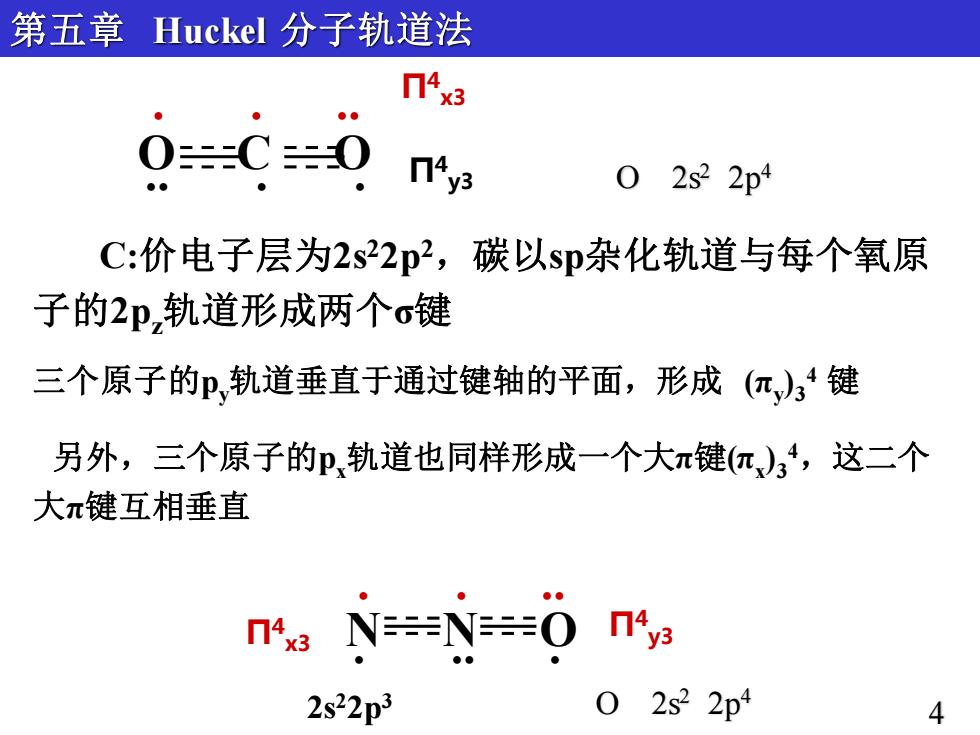
第五章 Huckel分子轨道法 n4x3 0=C=0 nys 0 2s22p4 C:价电子层为2s22p2,碳以sp杂化轨道与每个氧原 子的2p轨道形成两个σ键 三个原子的p,轨道垂直于通过键轴的平面,形成(π,)34键 另外,三个原子的P,轨道也同样形成一个大π键(π,)34,这二个 大π键互相垂直 4x3N=N=O04y 2s22p3 2s22p4 4
Π4 y3 O C O . . . . . . Π4 x3 Π4 Π y3 4 x3 N N O . . . . . . 第五章 Huckel 分子轨道法 C:价电子层为2s22p2,碳以sp杂化轨道与每个氧原 子的2pz轨道形成两个σ键 三个原子的py轨道垂直于通过键轴的平面,形成 (πy ) 3 4 键 另外,三个原子的px轨道也同样形成一个大π键(πx ) 3 4,这二个 大π键互相垂直 4 O 2s2 2p4 2s22p3 O 2s2 2p4
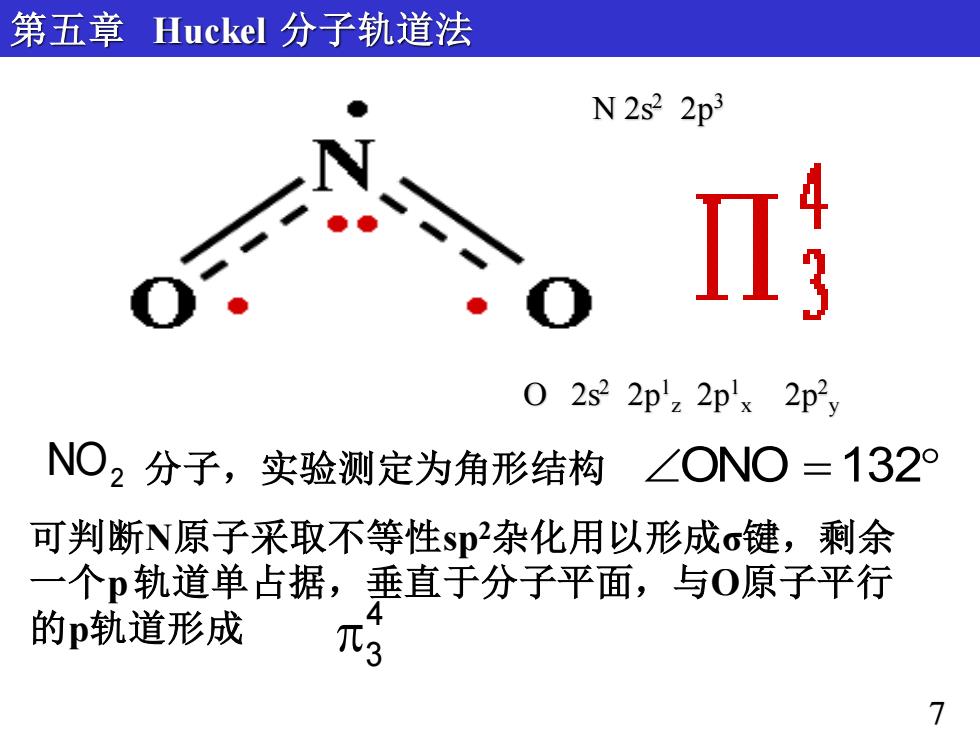
第五章Huckel分子轨道法 N2s2 2p3 02s22p'z2px2p2) NO2分子,实验测定为角形结构 ∠ONO=1329 可判断N原子采取不等性sp杂化用以形成o键,剩余 一个p轨道单占据,垂直于分子平面,与O原子平行 的p轨道形成 Ts 7
NO2 分子,实验测定为角形结构 ONO = 132 可判断N原子采取不等性sp2杂化用以形成σ键,剩余 一个p轨道单占据,垂直于分子平面,与O原子平行 的p轨道形成 4 3 第五章 Huckel 分子轨道法 7 O 2s2 2p1 z 2p1 x 2p2 y N 2s2 2p3

第五章Huckel分子轨道法 H,C-CH-CH-O n44 sp2 C 2s2 2p2 O 2s2 2p!2p's 2p2y R一 Π43 N2s2 2p3 8
Π4 4 H2C CH CH O . . . . O R C NH2 . . . Π4 3 第五章 Huckel 分子轨道法 8 sp2 C 2s2 2p2 O 2s2 2p1 z 2p1 x 2p2 y N 2s2 2p3

第五章Huckel分子轨道法 (四)无机共轭分子 1.二氧化氮NO2: sp2 N2s2 2p3 80022p 33 n43 能量的高低:33>43 此分子的结构为湾曲性;有未成对电子,应有顺磁性。 10
1. 二氧化氮 NO2 : (四)无机共轭分子 Π3 3 . . . N O O . Π4 3 . . . N O O . 能量的高低: Π4 Π 3 3 3 ﹥ 第五章 Huckel 分子轨道法 此分子的结构为湾曲性;有未成对电子,应有顺磁性。 10 sp2 N 2s2 2p3 O 2s2 2p4