
安前化零电子最素 新最大雪化零化工号院 第3章分析化学中的误差与数据处理 §3.1定量分析中的误差 定量分析的任务是准确测定试样中的组分的含量。在实际测定中,由于受分析方法、仪器、试 剂、操作技术等限制,即使采用最可靠的分析方法,使用最精密的仪器,由技术很熟练的人员进行操 作,也不可能得到绝对准确的结果:同一分析人员用同一方法对同一试样在相同条件下进行多次测定, 测定结果也总不能完全一致,分析结果在一定范围内波动。这是因为在任何测量过程中,误差是客观 存在的。因此,在实验过程中,应该了解分析过程中误差产生的原因及其规律性,以便采取相应的措 施,提高分析结果的准确度。同时,对测试数据进行正确的统计处理,以获得最可靠的数据信息。 一、准确度与误差(accuracy and error) 准确度:测量值(x)与真值()之间的符合程度。它说明测定结果的可靠性,用误差值来 量度: 误差是指测定值,与真实值“之差 绝对误差 E=X一H(I) 绝对误差不能完全地说明测定的准确度,即它没有与被测物质的质量联系起来。如果被称量物 质的质量分别为1.0000g和0.1000g,称量的绝对误差同样是0.0001g,则其含义就不同了,故分析结 果的准确度常用相对误差(E,)表示: E=X-1x109% (2) E,反映了误差在真实值中所占的比例,用来比较在各种情况下测定结果的准确度比较合理。 0.0001 如上述两物体的相对偏差分别为:E1= ×100%=0.01% 1.0000 0.0001 E2=0.1000 100%=0.1% 二、精密度与偏差(precision and deviation) 精密度:是在受控条件下多次测定结果的相互符合程度,表达了测定结果的重复性和再现性。用偏差 表示: 】绝对偏差、平均偏差和相对平均信差 (1)绝对偏差: d=x-x (2)平均偏差: a=∑r-4④ 第1页
分析化学电子教案 新疆大学化学化工学院 第 1 页 n x x d − = 第 3 章 分析化学中的误差与数据处理 §3.1 定量分析中的误差 定量分析的任务是准确测定试样中的组分的含量。在实际测定中,由于受分析方法、仪器、试 剂、操作技术等限制,即使采用最可靠的分析方法,使用最精密的仪器,由技术很熟练的人员进行操 作,也不可能得到绝对准确的结果;同一分析人员用同一方法对同一试样在相同条件下进行多次测定, 测定结果也总不能完全一致,分析结果在一定范围内波动。这是因为在任何测量过程中,误差是客观 存在的。因此,在实验过程中,应该了解分析过程中误差产生的原因及其规律性,以便采取相应的措 施,提高分析结果的准确度。同时,对测试数据进行正确的统计处理,以获得最可靠的数据信息。 一、准确度与误差(accuracy and error) 准确度:测量值(x)与真值()之间的符合程度。 它说明测定结果的可靠性,用误差值来 量度: 误差是指测定值 xi 与真实值μ之差 绝对误差 E = xi-μ (1) 绝对误差不能完全地说明测定的准确度,即它没有与被测物质的质量联系起来。如果被称量物 质的质量分别为 1.0000g 和 0.1000g,称量的绝对误差同样是 0.0001g,则其含义就不同了,故分析结 果的准确度常用相对误差(Er)表示: 100% − = x Er (2) Er 反映了误差在真实值中所占的比例,用来比较在各种情况下测定结果的准确度比较合理。 如上述两物体的相对偏差分别为: 100% 0.01% 1.0000 0.0001 Er1 = = ; 100% 0.1% 0.1000 0.0001 Er 2 = = 二、精密度与偏差(precision and deviation) 精密度:是在受控条件下多次测定结果的相互符合程度,表达了测定结果的重复性和再现性。用偏差 表示: 1 绝对偏差、平均偏差和相对平均偏差 (1)绝对偏差: d = x − x (2)平均偏差: (4)

令新化零电子教常 新最女零化季化工号院 (3)相对平均偏差d,-日x100%4 用平均偏差表示精密度比较简单,但不足之处是在一系列测定中,小的偏差测定总次数总是占 多数,而大的偏差的测定总是占少数。因此,在数理统计中,常用标准偏差表示精密度。 2标淮偏差和相对标准偏差 (1)总体标准偏差 当测定次数大量时(>30次),测定的平均值接近真值此时标准偏差用。表示: 2(x-0 0=1 (6) (2)样本标淮偏差 在实际测定中,测定次数有限,一般严30,此时,统计学中,用样本的标准偏差S来衡量分 析数据的分散程度: (x-x2 s=1\n-1 (7 总体一研究对象的全体(测定次数为无限次) 样本一从总体中随机抽出的一小部分 式中(m-1)为自由度,它说明在n次测定中,只有(1)个可变偏差,引入(-1),主要是为了校 正以样本平均值代替总体平均值所引起的误差 即 ==2 n (8) 而 S→ (3)样本的相对标准偏差—变异系数 5.%-Sx% x 9 3样本平均值的标淮偏差 S S:= (10) 此式说明:平均值的标准偏差按测定次数的平方根成正比例减少 第 2页
分析化学电子教案 新疆大学化学化工学院 第 2 页 = 100% x d dr ( 3 )相对平均偏差 (4) 用平均偏差表示精密度比较简单,但不足之处是在一系列测定中,小的偏差测定总次数总是占 多数,而大的偏差的测定总是占少数。因此,在数理统计中,常用标准偏差表示精密度。 2 标准偏差和相对标准偏差 (1)总体标准偏差 当测定次数大量时(>30 次),测定的平均值接近真值此时标准偏差用 表示: n x n i i = − = 1 2 ( ) (6) (2)样本标准偏差 在实际测定中,测定次数有限,一般 n<30 ,此时,统计学中,用样本的标准偏差 S 来衡量分 析数据的分散程度: 1 ( ) 1 2 − − = = n x x S n i i (7) 总体——研究对象的全体(测定次数为无限次) 样本——从总体中随机抽出的一小部分 式中(n-1)为自由度,它说明在 n 次测定中,只有(n-1)个可变偏差,引入(n-1),主要是为了校 正以样本平均值代替总体平均值所引起的误差 即 n x n x x i i n − − − → 2 2 ( ) 1 ( ) lim (8) 而 S → (3)样本的相对标准偏差——变异系数 % = % x S Sr (9) 3 样本平均值的标准偏差 n S S x = (10) 此式说明:平均值的标准偏差按测定次数的平方根成正比例减少

女前化零电子藏素 新最大香化零化工号院 三、准确度与精密度的关系 真值37.40 精密度 准确度 好 好 乙 好 稍差 丙 差 丁 很差 偶然性 36.0036.5037.0037.5038.00 由此可见: 精密度高,不一定准确度高 准确度高,一定要精密度好。 精密度是保证准确度的先决条件,精密度高的分析结果才有可能获得高准确度: 准确度是反映系统误差和随机误差两者的综合指标。 例:分析铁矿中铁含量,得如下数据:37.45%,37.20%,37.50%,37.30%,37.25%。计算此结果 的平均值、平均偏差、标准偏差、变异系数。 天-37.45%+37.20%+37.50%+37.30%+37.25%=37.34% 5 d= 0.11+0.14+0.16+0.04+0.09。 %=0.11% 5 s=-= 0.12+0.142+0.16>°+0.04+0.09yx100%=0.13% 5-1 C103% 四.误差的分类及减免误差的方法 l.系统误差(systermatic error)一可定误差(determinate error) (1)方法误差:拟定的分析方法本身不十分完善所造成: 如:反应不能定量完成:有副反应发生:谪定终点与化学计量点不一致:干扰组分存在等。 (2)仪器误差:主要是仪器本身不够准确或未经校准引起的: 如:量器(容量平、滴定管等)和仪表刻度不准。 第3页
分析化学电子教案 新疆大学化学化工学院 第 3 页 三、 准确度与精密度的关系 由此可见: 精密度高,不一定准确度高; 准确度高,一定要精密度好。 精密度是保证准确度的先决条件,精密度高的分析结果才有可能获得高准确度; 准确度是反映系统误差和随机误差两者的综合指标。 例:分析铁矿中铁含量,得如下数据:37.45% , 37.20%, 37.50% , 37.30% , 37.25%。计算此结果 的平均值、平均偏差、标准偏差、变异系数。 四. 误差的分类及减免误差的方法 1. 系统误差(systermatic error )——可定误差(determinate error) (1)方法误差:拟定的分析方法本身不十分完善所造成; 如:反应不能定量完成;有副反应发生;滴定终点与化学计量点不一致;干扰组分存在等。 (2)仪器误差:主要是仪器本身不够准确或未经校准引起的; 如:量器(容量平、滴定管等)和仪表刻度不准。 精密度 准确度 好 好 好 稍差 差 差 很差 偶然性 . % . % . % . % . % . % 37 34 5 37 45 37 20 37 50 37 30 37 25 = + + + + x = % 0.11% 5 1 0.11 0.14 0.16 0.04 0.09 = + + + + = = = n d d n i i % . % ( . ) ( . ) ( . ) ( . ) ( . ) 100 0 13 5 1 0 11 0 14 0 16 0 04 0 09 1 2 2 2 2 2 1 2 = − + + + + = − = = n d s n i i 100% 0.35% 37.34 0.13 = = = x s CV

令新化零电子教常 新最女零化季化工号院 (3)试剂误差:由于世纪不纯和蒸馏水中含有微量杂质所引起: (4)操作误差:主要指在正常操作情况下,由于分析工作者掌握操作规程与控制条件不当所引起的。 如滴定管读数总是偏高或偏低。 特性:重复性、恒定性、单向性、大小可测出并校正,故有称为可定误差。可以用对照试验、空白试 验、校正仪器等办法加以校正。 (1)采用对照试验检验可消除方法误差 对照试验:选择一种标准方法与所用方法作对比或选择与试样组成接近的标准试样作试验,找出校正 值加以校正。 (2)校正仪器或使用配套仪器消除仪器误差 对仪器在使用前加以校正,如砝码、容量瓶、滴定管、移液管等。 (3)采用空白试验和提纯试剂的方法消除试剂误差。 空白试验:指在不加试样的情况下,按照试样实验步骤和条件进行分析试验,所得结果称为空白值。 (4)同一个人操作消除人为误差 是否存在系统误差,常常通过回收试验加以检查。 回收试验:在测定试样某组分含量(x)的基础上,加入已知量的该组分(x2),再次测定其组分含量(x3)。 由回收试验所得数据计算出回收率。 回收率=二5×10% X2 由回收率的高低来判断有无系统误差存在。常量组分:一般为99%以上,微量组分:90-110% 2、随机误差(random error)一不可测误差(indeterminateerror) 产生原因与系统误差不同,它是由于某些偶然的因素所引起的。 如:测定时环境的温度、湿度和气压的微小波动,以其性能的微小变化等 特性:有时正、有时负,有时大、有时小,不确定性和不可避免性 (方向、大小不固定,似无规律)。 但在消除系统误差后,在同样条件下进行多次测定,则可发现其分布也是服从一定规律(统计学 正态分布),可用统计学方法来处理。 五、随机误差的分布服从正态分布 1、偶然误差的分布规律 当测定次数较多,在系统误差己经排除的情况下,随机误差的分布也有一定的规律。如以横坐标 表示随机误差的大小,以纵坐标表示随机误差出现的概率大小,当测定次数为无限多次时,则随机误 差服从正态分布规律。可用正态分布曲线(高斯分布的正态概率密度函数)表示: 第4页
分析化学电子教案 新疆大学化学化工学院 第 4 页 (3)试剂误差:由于世纪不纯和蒸馏水中含有微量杂质所引起; (4)操作误差:主要指在正常操作情况下,由于分析工作者掌握操作规程与控制条件不当所引起的。 如滴定管读数总是偏高或偏低。 特性:重复性、恒定性、单向性、大小可测出并校正,故有称为可定误差。可以用对照试验、空白试 验、校正仪器等办法加以校正。 (1)采用对照试验检验可消除方法误差 对照试验:选择一种标准方法与所用方法作对比或选择与试样组成接近的标准试样作试验,找出校正 值加以校正。 (2)校正仪器或使用配套仪器消除仪器误差 对仪器在使用前加以校正,如砝码、容量瓶 、滴定管、移液管等。 (3)采用空白试验和提纯试剂的方法消除试剂误差。 空白试验:指在不加试样的情况下,按照试样实验步骤和条件进行分析试验,所得结果称为空白值。 (4)同一个人操作消除人为误差 是否存在系统误差,常常通过回收试验加以检查。 回收试验:在测定试样某组分含量(x1)的基础上,加入已知量的该组分(x2),再次测定其组分含量(x3)。 由回收试验所得数据计算出回收率。 由回收率的高低来判断有无系统误差存在。常量组分: 一般为 99%以上,微量组分: 90~110%。 2、随机误差(random error)——不可测误差(indeterminate error) 产生原因与系统误差不同,它是由于某些偶然的因素所引起的。 如:测定时环境的温度、湿度和气压的微小波动,以其性能的微小变化等。 特性:有时正、有时负,有时大、有时小,不确定性和不可避免性 (方向、大小不固定,似无规律)。 但在消除系统误差后,在同样条件下进行多次测定,则可发现其分布也是服从一定规律(统计学 正态分布),可用统计学方法来处理。 五、随机误差的分布服从正态分布 1、偶然误差的分布规律 当测定次数较多,在系统误差已经排除的情况下,随机误差的分布也有一定的规律。如以横坐标 表示随机误差的大小,以纵坐标表示随机误差出现的概率大小,当测定次数为无限多次时,则随机误 差服从正态分布规律。可用正态分布曲线(高斯分布的正态概率密度函数)表示: 100% 2 3 1 − = x x x 回收率
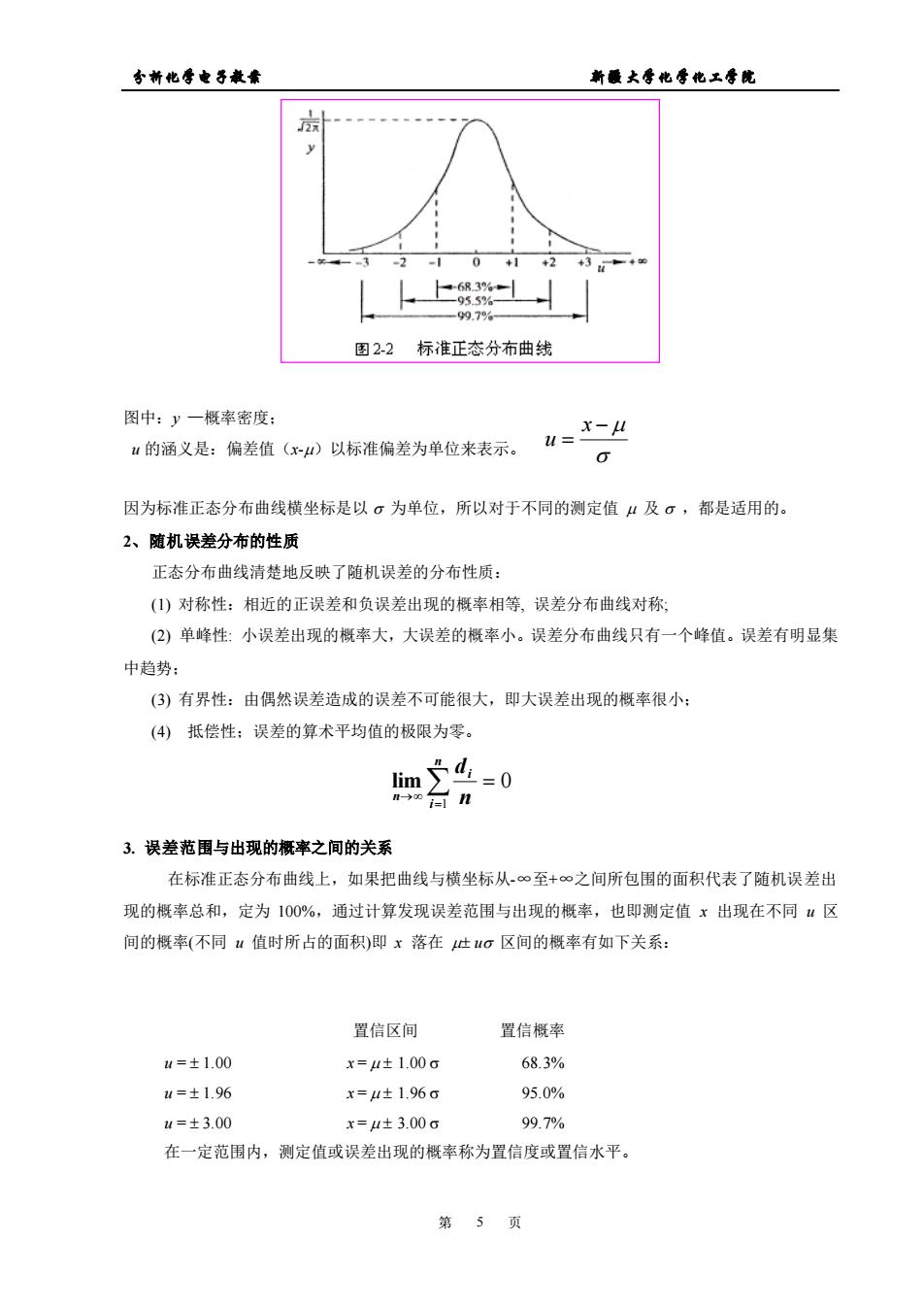
安前他零电子最素 新最大香化零化工号院 图22标准正态分布曲线 图中:y一概率密度 u的酒义是:偏差值(x)以标准偏差为单位来表示。 H=X-H 0 因为标准正态分布曲线横坐标是以。为单位,所以对于不同的测定值“及。,都是适用的。 2、随机误差分布的性质 正态分布曲线清楚地反映了随机误差的分布性质: ()对称性:相近的正误差和负误差出现的概率相等,误差分布曲线对称。 (②)单峰性:小误差出现的概率大,大误差的概率小。误差分布曲线只有一个峰值。误差有明显集 中趋势: (3)有界性:由偶然误差造成的误差不可能很大,即大误差出现的概率很小: (4)抵偿性:误差的算术平均值的极限为零。 =含-0 3.误差范围与出现的概率之间的关系 在标准正态分布曲线上,如果把曲线与横坐标从-∞至+©之间所包围的面积代表了随机误差出 现的概率总和,定为100%,通过计算发现误差范围与出现的概率,也即测定值x出现在不同“区 间的概率(不同“值时所占的面积)即x落在止“o区间的概率有如下关系: 置信区间 置信概率 u=±1.00 x=4±1.00c 68.3% =±1.96 x=4±1.96c 95.0% u=±3.00 x=u±3.00c 9979% 在一定范围内,测定值或误差出现的概率称为置信度或置信水平。 第5页
分析化学电子教案 新疆大学化学化工学院 第 5 页 图中:y —概率密度; u 的涵义是:偏差值(x-)以标准偏差为单位来表示。 因为标准正态分布曲线横坐标是以 为单位,所以对于不同的测定值 及 ,都是适用的。 2、随机误差分布的性质 正态分布曲线清楚地反映了随机误差的分布性质: (1) 对称性:相近的正误差和负误差出现的概率相等, 误差分布曲线对称; (2) 单峰性: 小误差出现的概率大,大误差的概率小。误差分布曲线只有一个峰值。误差有明显集 中趋势; (3) 有界性:由偶然误差造成的误差不可能很大,即大误差出现的概率很小; (4) 抵偿性;误差的算术平均值的极限为零。 3. 误差范围与出现的概率之间的关系 在标准正态分布曲线上,如果把曲线与横坐标从-∞至+∞之间所包围的面积代表了随机误差出 现的概率总和,定为 100%,通过计算发现误差范围与出现的概率,也即测定值 x 出现在不同 u 区 间的概率(不同 u 值时所占的面积)即 x 落在 u 区间的概率有如下关系: 置信区间 置信概率 u = 1.00 x = 1.00 68.3% u = 1.96 x = 1.96 95.0% u = 3.00 x = 3.00 99.7% 在一定范围内,测定值或误差出现的概率称为置信度或置信水平。 = → = n i i n n d 1 lim 0 − = x u

令新化零电子教常 新最女零化零化工季院 六、有限次测定中随机误差服从1分布 在实际测定中,测定次数都是有限的,实验所得到的只有x和S,但平均值毕竟不是真值,在多 数情况下,还需进一步解决平均值与真值间的关系,在一定的置信度下,由平均值估算出其值可能的 范围。 1.1分布曲线(实际测定中,用x、S代替4、) 有限次测定的随机误差并不服从正态分布,而是服从类似于正态分布的1分布,曲线与标准正态 分布曲线相似,纵坐标仍为概率密度,纵坐标则是新的统计量1表示 1=x-4 可衍生出: t=x-业n 1分布曲线随自由度∫(f=m-1)而变,当∫>20时,与正态分布曲线很近似,当∫一∞时 二者一致。1分布在分析化学中应用很多。 不同的f值及概率所对应的1值,已有统计学家计算出来,可由有关表22中查出。 2.平均值的置信区间 由1=天=业后得:4=x土 n 此式表示的是在一定概率下(如95%),以样本平均值为中心包括真值在内的范围,即平均值的 置倍区间。或在一定的概率下,真值将在测定平均值下附近的的一个区间即在下一 至 此式表明:平均值x与真值的关系,即说明平均值的可靠性。 平均值的置信区间取决于测定的精密度、测定次数和置信水平(概奉)。 置信区间的宽窄与置信度、测定值的精密度和测定次数有关,当测定值精密度↑(6值小,测定 次数愈多(1)时,置信区间,即平均值愈接近真值,平均值愈可靠。 置信度选择越高,置信区间越宽,其间包括真值的可能性也越大,在分析工作中常规定为95%。 例1:测定Si02的质量分数,得到下列数据,求平均值、标准偏差、置信度分别为90%和95% 时平均值的置信区间。 28.62,28.59,28.51,28.4828.52.28.63 解: 王=28.62+28.59+28.51+28.48+28.52+28.63=2856 5=@0o+10.03+00s2+0.0s'+004P+0.07-006 6-1 第6页
分析化学电子教案 新疆大学化学化工学院 第 6 页 六、有限次测定中随机误差服从 t 分布 在实际测定中,测定次数都是有限的,实验所得到的只有 x 和 S,但平均值毕竟不是真值,在多 数情况下,还需进一步解决平均值与真值间的关系,在一定的置信度下,由平均值估算出真值可能的 范围。 1. t 分布曲线 (实际测定中,用 x 、S 代替 、) 有限次测定的随机误差并不服从正态分布,而是服从类似于正态分布的 t 分布,曲线与标准正态 分布曲线相似,纵坐标仍为概率密度,纵坐标则是新的统计量 t 表示 S x t − = 可衍生出: t 分布曲线随自由度 f ( f = n - 1)而变,当 f >20 时,与正态分布曲线很近似,当 f →∞时, 二者一致。t 分布在分析化学中应用很多。 不同的 f 值及概率所对应的 t 值,已有统计学家计算出来,可由有关表 2-2 中查出。 2. 平均值的置信区间 由 得: 此式表示的是在一定概率下(如 95%),以样本平均值为中心包括真值在内的范围,即平均值的 置信区间。或在一定的概率下,真值将在测定平均值 x 附近的的一个区间即在 至 之间存在,把握程度为 95%。 此式表明:平均值 x 与真值的关系,即说明平均值的可靠性。 平均值的置信区间取决于测定的精密度、测定次数和置信水平(概率)。 置信区间的宽窄与置信度、测定值的精密度和测定次数有关,当测定值精密度↑(s 值小),测定 次数愈多(n↑)时,置信区间↓,即平均值愈接近真值,平均值愈可靠。 置信度选择越高,置信区间越宽,其间包括真值的可能性也越大,在分析工作中常规定为 95%。 例 1:测定 SiO2 的质量分数,得到下列数据,求平均值、标准偏差、置信度分别为 90%和 95% 时平均值的置信区间。 28.62, 28.59, 28.51, 28.48, 28.52, 28.63 解: n s x t − μ = n s x t − = n ts = x n ts x − n ts x + 28.56 6 28.62 28.59 28.51 28.48 28.52 28.63 = + + + + + x = 0.06 6 1 (0.06) (0.03) (0.05) (0.08) (0.04) (0.07) 2 2 2 2 2 2 = − + + + + + s =

女前化零电子藏素 新最大香化零化工号院 查表2-2置信度为90%,n=6时,1=2.015。 4=28.56±2.571x0.06=28.56士0.05 6 置信度为95%时: 4=28.56±2571x0.06-28.56±0.07 得到启示:置信度1,置信区间↑。 例2:测定钢中含铬量时,先测定两次,测得的质量分数为1.12%和1.15%:再测定三次,测得的数据 为1.11%,1.16%和1.12%。计算两次测定和五次测定平均值的置信区间(95%置信度)。 解:n=2时 F=1.12%+1.15% =1.14% 0015'+0015_0.021 s= 2-1 查表2-2,得5%=12.7。 W。=l14%±27x0021-L14%t019% 2 n=5时:查表2-2,得19%=2.78。 x=126+1.15%+1.11%+1.16%+1.12%=L13% 5 =2-=a022 n-1 W。=L13%±278x002=.13%±Q03% 5 启示:在一定测定次数范围内,适当增加测定次数,可使置信区间显著缩小,即可使测定的平均值与 总体平均值μ接近 §3.2有效数字及其运算规则 1.有效数字的意义和位数 (1)有效数字:所有准确数字和一位可疑数字(实际能测到的数字) (2)有效位数及数据中的0“ 1.0005, 五位有效数字 0.5000, 31.05% 四位有效数字 0.0540, 1.86 三位有效数字 第7页
分析化学电子教案 新疆大学化学化工学院 第 7 页 查表 2-2 置信度为 90%,n = 6 时,t = 2.015。 置信度为 95% 时: 得到启示:置信度↑,置信区间↑。 例2:测定钢中含铬量时,先测定两次,测得的质量分数为1.12%和1.15%;再测定三次, 测得的数据 为1.11%, 1.16%和1.12%。计算两次测定和五次测定平均值的置信区间(95%置信度)。 解: n = 2 时 查表 2-2,得 t95% = 12.7。 n = 5 时:查表 2-2,得 t95% = 2.78。 启示:在一定测定次数范围内,适当增加测定次数,可使置信区间显著缩小,即可使测定的平均值与 总体平均值μ接近 §3.2 有效数字及其运算规则 1. 有效数字的意义和位数 (1)有效数字:所有准确数字和一位可疑数字(实际能测到的数字) (2)有效位数及数据中的“ 0 ” 1.0005, 五位有效数字 0.5000, 31.05% 四位有效数字 0.0540, 1.86 三位有效数字 28.56 0.05 6 2.571 0.06 28.56 = = 28.56 0.07 6 2.571 0.06 28.56 = = . % . % . % . % . % . % x 1 13 5 1 12 1 15 1 11 1 16 1 12 = + + + + = 0.022 1 ( ) 2 = − − = n x x s . % . % . . W . % 1 13 0 03 5 2 78 0 022 Cr 1 13 = = 1.14% 2 1.12% 1.15% = + x = 0.021 2 1 (0.015) (0.015) 2 2 = − + s = . % . % . . W . % 1 14 0 19 2 12 7 0 021 Cr 1 14 = =

令新化零电子教常 新最女零化季化工号院 0.0054 0.40% 两位有效数字 0.5, 0.002% 一位有效数字 2.有效数字的表达及运算规则 (1)记录一个测定值时,只保留一位可疑数据, (2)整理数据和运算中弃取多余数字时,采用“数字修约规则”: 四舍六入五考虑 五后非零则进一 五后皆零视奇偶 五前为奇则进一 五前为偶则舍弃 不许连续修约 (3)加减法:以小数点后位数最少的数据的位数为准,即取决于绝对误差最大的数据位数: (4)乘除法:由有效数字位数最少者为准,即取决于相对误差最大的数据位数: (5)对数:对数的有效数字只计小数点后的数字,即有效数字位数与真数位数一致: (6)常数:常数的有效数字可取无限多位: (7)第一位有效数字等于或大于8时,其有效数字位数可多算一位: (8)在计算过程中,可暂时多保留一位有效数字。 (9)误差或偏差取1~2位有效数字即可。 §3.3分析结果的数据处理 为什么要对数据进行处理? 个别偏离较大的数据(称为离群值或极值)是保留还是该弃去? 测得的平均值与真值(或标准值)的差异,是否合理? 相同方法测得的两组数据或用两种不同方法对同一试样测得的两组数据间的差异是否在允许的 范围内? 数据进行处理包括哪些方面? 可疑数据的取舍—过失误差的判断 分析方法的准确度(可靠性)一系统误差的判断 一、可疑数据的取舍 1.G检验法(Grubbs法) 设有n各数据2.G检验法(Grubbs法) 设有n各数据,从小到大为,2,. 其中x或为可疑数据: (I)计算X(包括可疑值x、在内)人、xX及S 第8页
分析化学电子教案 新疆大学化学化工学院 第 8 页 0.0054, 0.40% 两位有效数字 0.5, 0.002% 一位有效数字 2. 有效数字的表达及运算规则 (1)记录一个测定值时,只保留一位可疑数据, (2)整理数据和运算中弃取多余数字时,采用“数字修约规则”: 四舍六入五考虑 五后非零则进一 五后皆零视奇偶 五前为奇则进一 五前为偶则舍弃 不许连续修约 (3)加减法:以小数点后位数最少的数据的位数为准,即取决于绝对误差最大的数据位数; (4)乘除法:由有效数字位数最少者为准,即取决于相对误差最大的数据位数; (5)对 数:对数的有效数字只计小数点后的数字,即有效数字位数与真数位数一致; (6)常 数:常数的有效数字可取无限多位; (7)第一位有效数字等于或大于 8 时,其有效数字位数可多算一位; (8)在计算过程中,可暂时多保留一位有效数字; (9)误差或偏差取 1~2 位有效数字即可。 §3.3 分析结果的数据处理 为什么要对数据进行处理? 个别偏离较大的数据(称为离群值或极值)是保留还是该弃去? 测得的平均值与真值(或标准值)的差异,是否合理? 相同方法测得的两组数据或用两种不同方法对同一试样测得的两组数据间的差异是否在允许的 范围内? 数据进行处理包括哪些方面? 可疑数据的取舍——过失误差的判断 分析方法的准确度(可靠性)——系统误差的判断 一、可疑数据的取舍 1. G 检验法(Grubbs 法) 设有 n 各数据 2. G 检验法(Grubbs 法) 设有 n 各数据,从小到大为 x1, x2, x3,. xn; 其中 x1 或 xn 为可疑数据: (1) 计算 x (包括可疑值 x1、 xn 在内)、∣x 可疑- x ∣及 S;

安前他零电子最素 新最大雪化雪化工零院 G4=氏~ (2)计算G: S (3)查G值表得GP (4)比较G#与Gp: 若G+2GwP则舍去可疑值: G#G则舍去可疑值: G#Q舍弃该数据,(过失误差造成) 若Q≤Q保留该数据,(偶然误差所致) 例:测定某药物中C0的含量(104)得到结果如下: 1.25,1.27,1.31,1.40, 用Grubbs法和Q值检验法判断1.40是否保留。 解:①用Grubbs法:x=1.31:s=0.066 G计算 140-1.31=1.36 0.066 第9页
分析化学电子教案 新疆大学化学化工学院 第 9 页 (2) 计算 G: s x x G i − 计 = (3) 查 G 值表得 G,P (4) 比较 G 计与 G,P: 若 G 计 G,P则舍去可疑值; G 计 G 表则舍去可疑值; G 计 Qx 舍弃该数据, (过失误差造成) 若 Q ≤ Qx 保留该数据, (偶然误差所致) 例:测定某药物中 Co 的含量(10-4)得到结果如下: 1.25, 1.27, 1.31, 1.40, 用 Grubbs 法和 Q 值检验法判断 1.40 是否保留。 解:① 用 Grubbs 法: x = 1.31 ; s = 0.066 1 2 1 1 1 x x x x Q x x x x Q n n n n − − = − − = − 或 1 36 0 066 1 40 1 31 . . . . = − G计算 =

令新化零电子教常 新最女零化季化工号院 查表2-3,置信度选95%,n=4,G表=1.46 G计算<G表 故1.40应保留 ②用Q值检验法:可疑值x 0*=-=40-131=0.60 xm-x11.40-1.25 查表2-4,n=4, Q0.90=0.76 Qu<Q90 故1.40应保留。 讨论: (1)Q值法不必计算x及s,使用比较方便: (2)Q值法在统计上有可能保留离群较远的值。 (3)Grubbs法引入s,判断更准确。 (4不能追求精密度而随意丢弃数据:必须进行检验: 例:三个测定值,40.12,40.16和40.18 ±合-4015±4031-4015t0 3 置信区间:40.07、40.23之间(置信度为95%)。 舍去40.12 ±=40.17±2-71x0.014=40.170.15 n 2 置信区间:40.0440.30,变大 总之,出现离群数据时,应从技术上查明原因,然后再进行统计检验,切忌任意舍弃 二.平均值与标准值的比较(检验方法的准确度) 1.为了检验一个分析方法是否可靠,是否有足够的准确度,常用已知含量的标准试样进行实验,用 检验法将测定的平均值与已知值(标样值)比较, -n S 若1#≥1则X与有显著性差异(方法不可靠 1<1则x与“无显著性差异(方法可靠》 三.两组平均值的比较 当需要对两个分析人员测定相同试样所得结果进行评价,或需对两种方法进行比较,检验两种方 法是否存在显著性差异,即是否存在系统误差时,可选用!检验法进行检验。 (1)先用F检验法检验两组数据精密度S体小*,有无显著性差异(方法之间) 第10页
分析化学电子教案 新疆大学化学化工学院 第 10 页 查表 2-3,置信度选 95%,n = 4,G 表 = 1.46 G 计算 < G 表 故 1.40 应保留。 ② 用 Q 值检验法:可疑值 xn 查表 2-4, n = 4 , Q0.90 = 0.76 Q 计算 < Q0.90 故 1.40 应保留。 讨论: (1) Q 值法不必计算 x 及 s,使用比较方便; (2) Q 值法在统计上有可能保留离群较远的值。 (3) Grubbs 法引入 s ,判断更准确。 (4) 不能追求精密度而随意丢弃数据;必须进行检验; 例:三个测定值,40.12, 40.16 和 40.18 置信区间: 40.07 ~ 40.23 之间(置信度为 95%)。 舍去 40.12 置信区间:40.04~40.30,变大。 总之,出现离群数据时,应从技术上查明原因,然后再进行统计检验,切忌任意舍弃。 二. 平均值与标准值的比较(检验方法的准确度) 1. 为了检验一个分析方法是否可靠,是否有足够的准确度,常用已知含量的标准试样进行实验,用 t 检验法将测定的平均值与已知值(标样值)比较。 n S x t − 计 = 若 t 计 t 表 则 x 与 有显著性差异(方法不可靠) t 计 < t 表 则 x 与 无显著性差异(方法可靠) 三. 两组平均值的比较 当需要对两个分析人员测定相同试样所得结果进行评价,或需对两种方法进行比较,检验两种方 法是否存在显著性差异,即是否存在系统误差时,可选用 t 检验法进行检验。 (1)先用 F 检验法检验两组数据精密度 S1(小)、S2(大) 有无显著性差异(方法之间) 0 60 1 40 1 25 1 40 1 31 1 1 . . . . . = − − = − − = − x x x x Q n n n 计算 40 15 0 08 3 4 3 0 031 40 15 . . . . . = = n ts x 40 17 0 13 2 12 71 0 014 40 17 . . . . . = = n ts x