
第3章氢化非晶硅薄膜晶体管 简介 3.1a-Si:H半导体的物理基础 3.2a-Si:HTFT的工作原理与特性 3.3a-Si:HTFT中的关键材料 3.4a-Si:HTFT电性能的稳定性
第3章 氢化非晶硅薄膜晶体管 简介 3.1 α-Si:H半导体的物理基础 3.2 α-Si:H TFT 的工作原理与特性 3.3 α-Si:H TFT中的关键材料 3.4 α-Si:H TFT 电性能的稳定性

知识点 1.a-Si结构。 2.电子定域态。 3.a-SiH的态密度分布。 4.a-Si:H结构中存在弱的SiSi键、悬挂键以及被H饱和的Si-H键,它们之间达到一种 亚稳平衡。 5.a-Si:H的光吸收特性。 6.a-SiH的掺杂。 7.多重陷阱俘获-释放模型。 8.背沟刻蚀型结构和刻蚀阻挡型结构。 9.a-Si:HTFT的特性:开态电流、载流子迁移率、关态电流、源漏接触电阻。 10.a-Si:H薄膜和a-SiNx:H薄膜的制备工艺及材料特性。 11.a-Si:HTFT在直流偏压下阈值电压漂移。 12.a-Si:HTFT阈值电压变化量与时间的关系
1. α-Si结构。 2. 电子定域态。 3. α-Si:H的态密度分布。 4. α-Si:H结构中存在弱的Si-Si键、悬挂键以及被H饱和的Si-H键,它们之间达到一种 亚稳平衡。 5. α-Si:H的光吸收特性。 6. α-Si:H的掺杂。 7. 多重陷阱俘获-释放模型。 8. 背沟刻蚀型结构和刻蚀阻挡型结构。 9. α-Si:H TFT的特性:开态电流、载流子迁移率、关态电流、源漏接触电阻。 10. α-Si:H薄膜和α-SiNx:H薄膜的制备工艺及材料特性。 11.α-Si:H TFT在直流偏压下阈值电压漂移。 12. α-Si:H TFT阈值电压变化量与时间的关系。 知识点

简介 。 1975年,Spear&Lecomber小组成功地实现了对非晶硅材料的 p型和n型掺杂。 1977年,RCA实验室的Carlson等做出了第一个非晶硅太阳电 池。 ·1979年,Lecomber做出第一个a-Si TFT(液晶显示)
简介 • 1975年,Spear & Lecomber小组成功地实现了对非晶硅材料的 p型和n型掺杂。 • 1977年,RCA 实验室的Carlson 等做出了第一个非晶硅太阳电 池。 • 1979年,Lecomber做出第一个a-Si TFT(液晶显示)
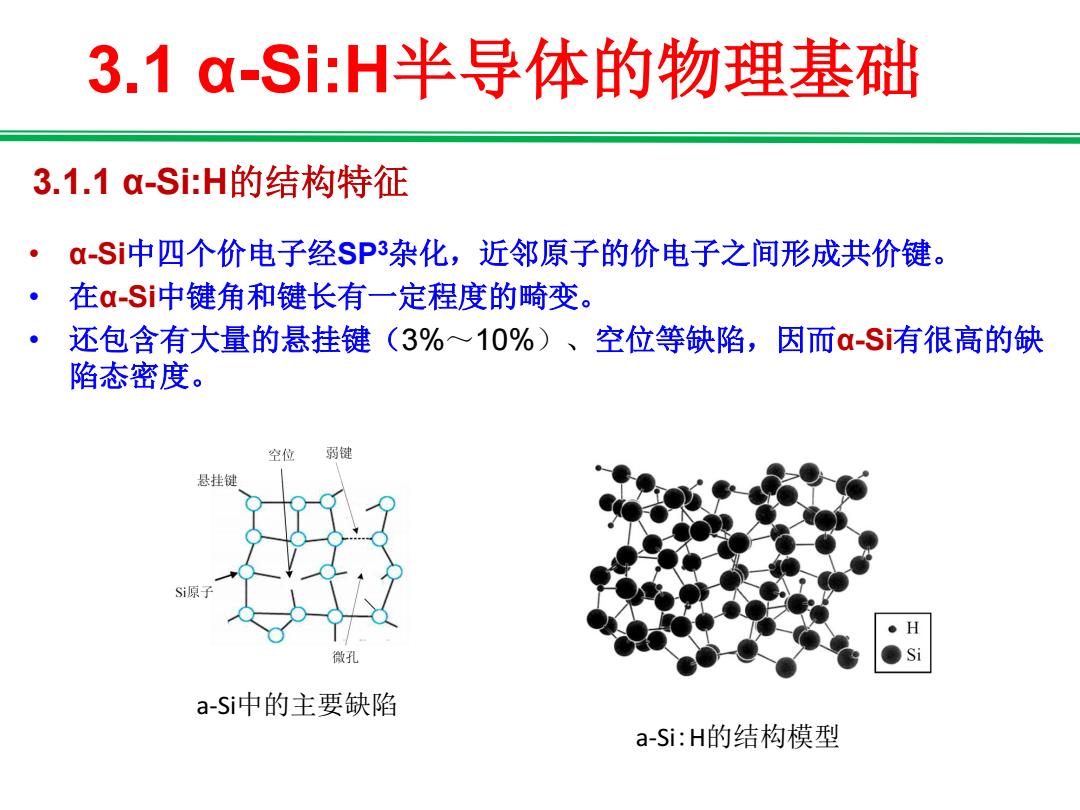
3.1q-Si:H半导体的物理基础 3.1.1a-SiH的结构特征 a-Si中四个价电子经SP3杂化,近邻原子的价电子之间形成共价键。 在α-Si中键角和键长有一定程度的畸变。 还包含有大量的悬挂键(3%~10%)、空位等缺陷,因而α-Si有很高的缺 陷态密度。 空位弱键 悬挂键 Si原了 H 微孔 ●Si a-Si中的主要缺陷 a-Si:H的结构模型
3.1 α-Si:H半导体的物理基础 3.1.1 α-Si:H的结构特征 • α-Si中四个价电子经SP3杂化,近邻原子的价电子之间形成共价键。 • 在α-Si中键角和键长有一定程度的畸变。 • 还包含有大量的悬挂键(3%~10%)、空位等缺陷,因而α-Si有很高的缺 陷态密度。 a-Si中的主要缺陷 a-Si:H的结构模型
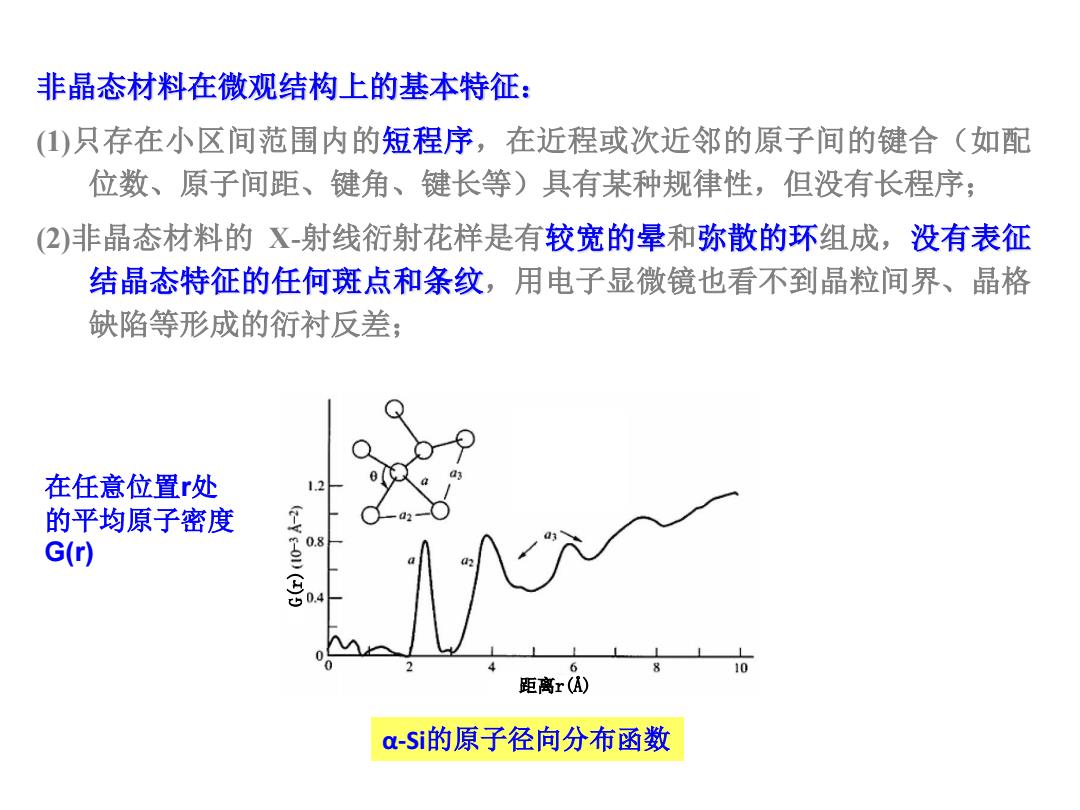
非晶态材料在微观结构上的基本特征: (1)只存在小区间范围内的短程序,在近程或次近邻的原子间的键合(如配 位数、原子间距、键角、键长等)具有某种规律性,但没有长程序; 2)非晶态材料的X-射线衍射花样是有较宽的晕和弥散的环组成,没有表征 结晶态特征的任何斑点和条纹,用电子显微镜也看不到晶粒间界、晶格 缺陷等形成的衍衬反差: 在任意位置r处 的平均原子密度 G(r) 10 距离r(A) a-Si的原子径向分布函数
非晶态材料在微观结构上的基本特征: (1)只存在小区间范围内的短程序,在近程或次近邻的原子间的键合(如配 位数、原子间距、键角、键长等)具有某种规律性,但没有长程序; (2)非晶态材料的 X-射线衍射花样是有较宽的晕和弥散的环组成,没有表征 结晶态特征的任何斑点和条纹,用电子显微镜也看不到晶粒间界、晶格 缺陷等形成的衍衬反差; 距离r(Å) G(r) α-Si的原子径向分布函数 在任意位置r处 的平均原子密度 G(r)

3.1.2a-SiH的电子态和能带模型 1957年,Anderson定域化理论。 60年代,Mott-CFO能带模型。 1977年,Mott,Anderson获诺贝尔奖。 非晶材料的能带一Mot模型 SIR NEVILL F.MOTT (1905-1996) 1977 Nobel Laureate in Physics for their fundamental theoretical investigations of the electronic structure of magnetic and disordered systems
SIR NEVILL F. MOTT (1905-1996) 1977 Nobel Laureate in Physics for their fundamental theoretical investigations of the electronic structure of magnetic and disordered systems. 非晶材料的能带——Mott模型 1957年,Anderson 定域化理论。 60年代,Mott-CFO 能带模型。 1977年,Mott,Anderson 获诺贝尔奖。 3.1.2 α-Si:H的电子态和能带模型

1.无序体系中电子态的定域化 在理想周期势场中,叠加无规势场V。,安德森提出了一个区分扩展态和定域 态的定义:假设一个电子在t=0时处在格点处的某个态中,由于第二项微扰 的作用,电子的波函数随时间变化。如t→∞时在原来状态找到电子的几率为 零,表明电子已扩散走了,就是扩展态;如果t→∞时几率为有限值,就是定 域态。 能量 晶态 V。一无序势 B=2ZI VB大到一定程 态密度 能量 度→定域化 V0:无规势场围绕平均值的变化 非晶态 B:能带宽度 态密度
• 在理想周期势场中,叠加无规势场V0,安德森提出了一个区分扩展态和定域 态的定义:假设一个电子在t=0时处在n格点处的某个态中,由于第二项微扰 的作用,电子的波函数随时间变化。如t→∞时在原来状态找到电子的几率为 零,表明电子已扩散走了,就是扩展态;如果t→∞时几率为有限值,就是定 域态。 V0:无规势场围绕平均值的变化 B:能带宽度 1.无序体系中电子态的定域化
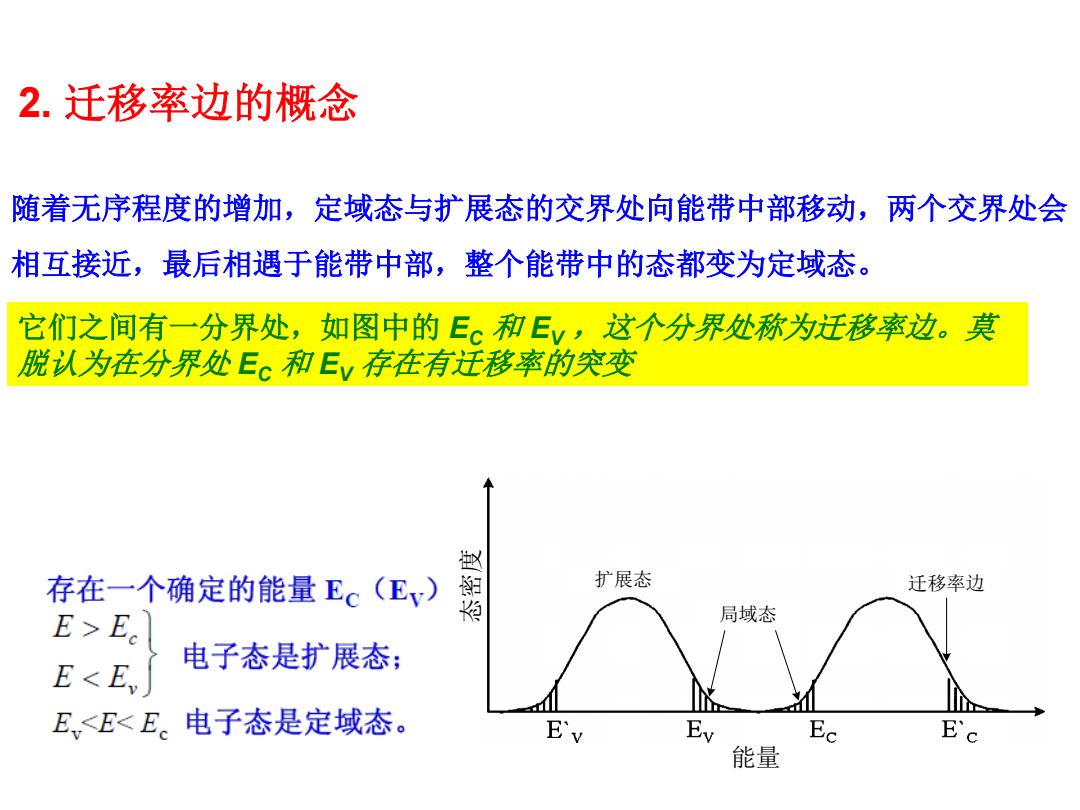
2.迁移率边的概念 随着无序程度的增加,定域态与扩展态的交界处向能带中部移动,两个交界处会 相互接近,最后相遇于能带中部,整个能带中的态都变为定域态。 它们之间有一分界处,如图中的Ec和Ey,这个分界处称为迁移率边。莫 脱认为在分界处E。和E存在有迁移率的突变 存在一个确定的能量Ec(Ev) 扩展态 迁移率边 ExE 局域态 E<E 电子态是扩展态: E,<E<E。电子态是定域态。 Ev Ec 能量
2. 迁移率边的概念 随着无序程度的增加,定域态与扩展态的交界处向能带中部移动,两个交界处会 相互接近,最后相遇于能带中部,整个能带中的态都变为定域态。 它们之间有一分界处,如图中的 EC 和 EV ,这个分界处称为迁移率边。莫 脱认为在分界处 EC 和 EV 存在有迁移率的突变 态 密 度 能量 局域态 扩展态 迁移率边
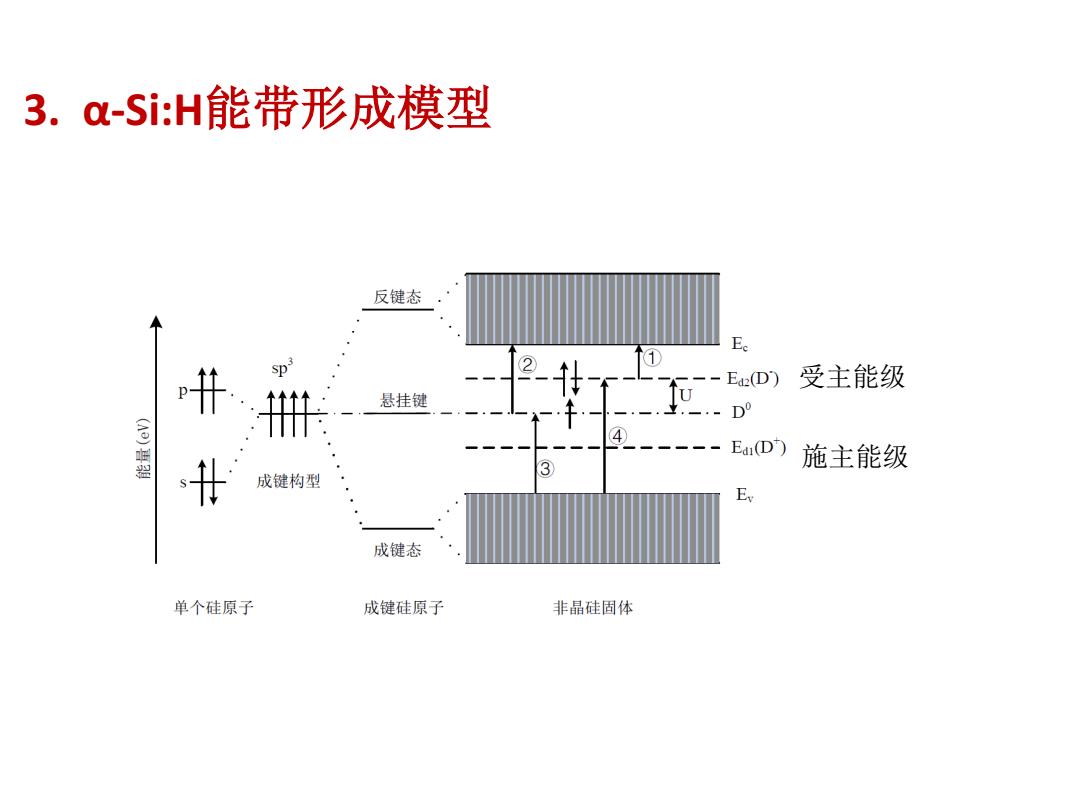
3.a-Si:H能带形成模型 反键态 E 1 --ED)受主能级 悬挂键 4-----Ea(D) 壮 施主能级 成键构型 成键态 单个硅原子 成键硅原子 非晶硅固体
3. α-Si:H能带形成模型 受主能级 施主能级
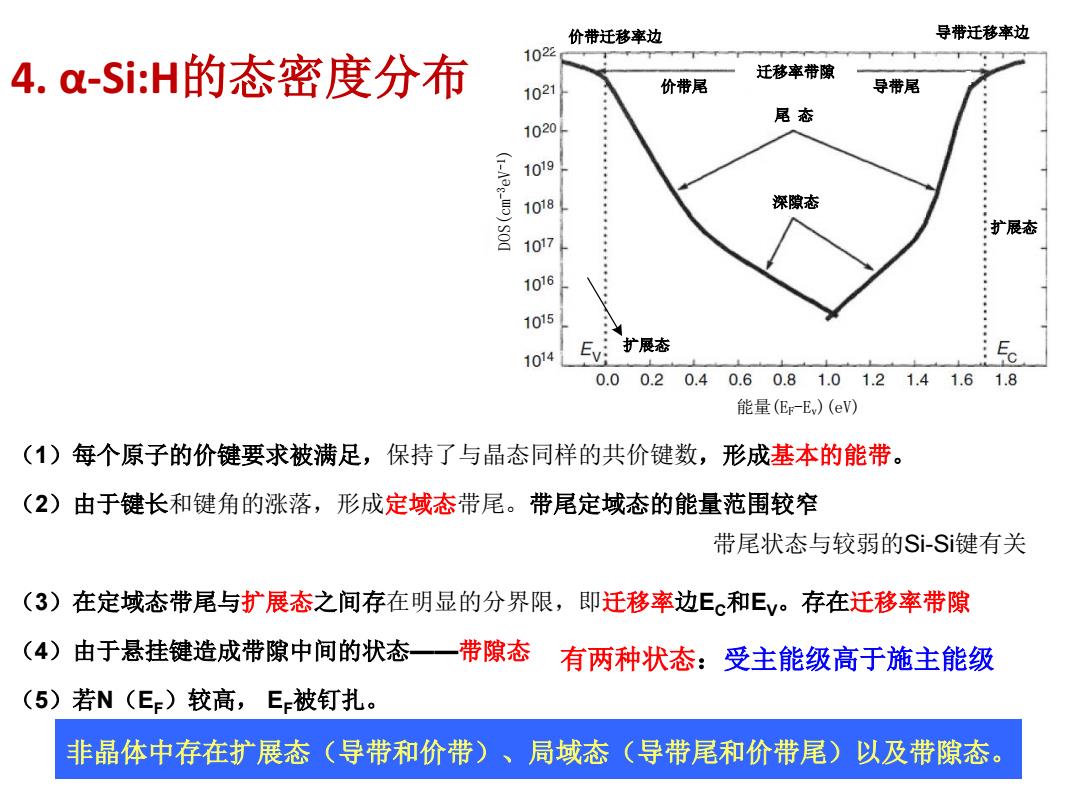
价带迁移率边 导带迁移率边 1022 4.a-Si:H的态密度分布 迁移率带隙 1021 价带尾 导带尾 尾态 10201 1019 1018 深隙态 扩展态 1017 1016 1015 1014 Ev: 扩展态 0.0 0.20.40.60.81.01.21.41.61.8 能量(Er-Ev)(eV) (1)每个原子的价键要求被满足,保持了与晶态同样的共价键数,形成基本的能带。 (2)由于键长和键角的涨落,形成定域态带尾。带尾定域态的能量范围较窄 带尾状态与较弱的Si-Si键有关 (3)在定域态带尾与扩展态之间存在明显的分界限,即迁移率边E。和Ey。存在迁移率带隙 (4)由于悬挂键造成带隙中间的状态一一带隙态 有两种状态:受主能级高于施主能级 (5)若N(EF)较高,E被钉扎。 非晶体中存在扩展态(导带和价带)、局域态(导带尾和价带尾)以及带隙态
(1)每个原子的价键要求被满足,保持了与晶态同样的共价键数,形成基本的能带。 (2)由于键长和键角的涨落,形成定域态带尾。带尾定域态的能量范围较窄 (3)在定域态带尾与扩展态之间存在明显的分界限,即迁移率边EC和EV。存在迁移率带隙 (4)由于悬挂键造成带隙中间的状态——带隙态 (5)若N(EF)较高, EF被钉扎。 带尾状态与较弱的Si-Si键有关 非晶体中存在扩展态(导带和价带)、局域态(导带尾和价带尾)以及带隙态。 有两种状态:受主能级高于施主能级 4. α-Si:H的态密度分布 能量(EF-Ev)(eV) 深隙态 尾 态 价带尾 导带尾 迁移率带隙 价带迁移率边 导带迁移率边 扩展态 扩展态 DOS(cm-3eV-1)