
第六章循环码的译码 陆以勤 2005年5月
第六章 循环码的译码 陆以勤 2005年5月

一、循环码译码的原理 线性分组码的译码:标准阵列译码,伴随式译码 译码电路复杂 r→s计算电路 s→e译码表 r-e电路
一、循环码译码的原理 ◼ 线性分组码的译码:标准阵列译码,伴随式译码 译码电路复杂 r→s计算电路 s→e译码表 r- e电路 ....... r c

一、循环码译码的原理-线性分组码中求伴随式的电路 1110100 例1:[7,4,3]循环汉明码,g(X)=x3+x+1,H= 0111010 1101001 T 1110100 s=rHT=(rers r4r3r2rro) 0111010 fo+rs+ra+r2T(2S0) r5+r4+r3+r1 1101001 r6+r5+r3+ro ro r r2 4 r(x) 60 S2
一、循环码译码的原理----线性分组码中求伴随式的电路 例1:[7,4,3] 循环汉明码,g(x)=x3+x+1,H= 1110100 0111010 1101001 s = r HT= ( r6 r5 r4 r3 r2 r1 r0 ) T r6 + r5 + r4 + r2 r5 + r4 + r3 + r1 r6 + r5 + r3 + r0 = T = (s2 s1 s0 ) r0 + r1 r 2 r 3 r 4 r 5 r 6 + + r(x) s0 s1 s2 1110100 0111010 1101001

一、循环码译码的原理--利用循环码的特殊性简化电路 s=rHT H=[-PTIn-k]=[-(1(X)T-(r2(X)T..-(k(X)Tn-k] 其中,r,x)=-xni(modg(x)(i=1,2…,。 x-1 x-2 HT≡ x- ≡Ln] 七-k-l mod g(x) 1 s≡HT=r(modg(x) s(X)≡rx)≡(c(x)+e(x)≡e(X)(modg(X) 定理1:由g(X)生成的循环码,()的伴随式s()满足: s(x)=r(x)=e(x)(mod g(x)) 因此,求S(x)可用除以gx的电路实现。这样可把n级寄存器降为n-k级
一、循环码译码的原理----利用循环码的特殊性简化电路 ◼ s rHT H=[-P T In-k ]=[-(r1 (x))T -(r2 (x))T…-(rk (x))T In-k ] 其中,ri (x) - x n-i (mod g(x)) (i=1,2,...,k)。 [I ] 1 ... ... H n 1 2 1 T − − − − − n k n k n n x x x x mod g(x) s rHTr (mod g(x)) s(x) r(x) (c(x)+e(x)) e(x) (mod g(x)) 定理1:由g(x)生成的循环码,r(x)的伴随式s (x)满足: s(x) r(x) e(x) (mod g(x)) 因此,求S (x)可用除以g(x)的电路实现。这样可把n级寄存器降为n-k级
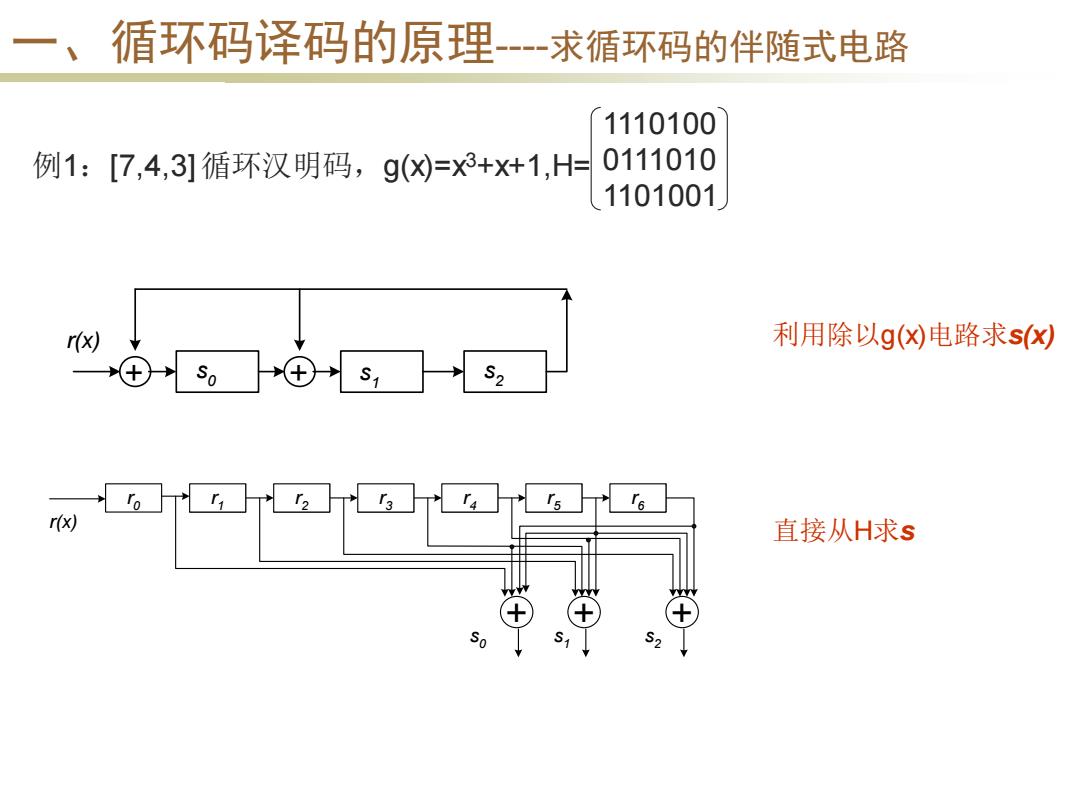
一、循环码译码的原理--求循环码的伴随式电路 1110100 例1:[7,4,3]循环汉明码,g()=x3+x+1,H= 0111010 1101001 r(x) 利用除以g()电路求s(x) So 52 r(x) 直接从H求s So S1
一、循环码译码的原理----求循环码的伴随式电路 r0 + r1 r 2 r 3 r 4 r 5 r 6 + + r(x) s0 s1 s2 例1:[7,4,3] 循环汉明码,g(x)=x3+x+1,H= 1110100 0111010 1101001 + + r(x) s0 s1 s2 直接从H求s 利用除以g(x)电路求s(x)
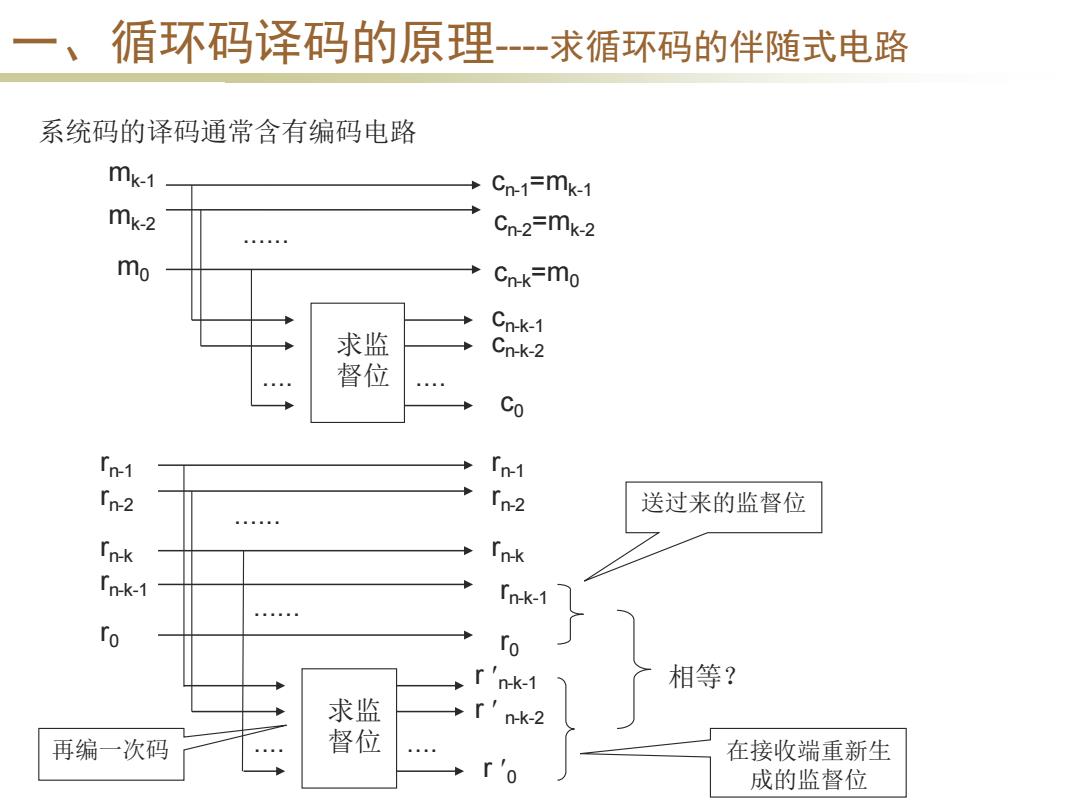
一、循环码译码的原理-求循环码的伴随式电路 系统码的译码通常含有编码电路 mk-1 Cn-1=mk-1 mk-2 Cn-2=mk-2 mo Cnk=mo Cn-k-1 求监 Cn-k-2 督位 Co -1 In Tn-2 送过来的监督位 Tn-k nk-1 In-k- ro ro n-k-1 相等? 求监 n-k-2 再编一次码 督位 在接收端重新生 成的监督位
一、循环码译码的原理----求循环码的伴随式电路 系统码的译码通常含有编码电路 ...... .... mk-1 mk-2 m0 cn-1=mk-1 cn-2=mk-2 cn-k=m0 cn-k-1 cn-k-2 .... c0 求监 督位 ...... .... .... 求监 督位 rn-1 rn-2 rn-k rn-1 rn-k rn-2 ...... rn-k-1 r0 rn-k-1 r0 r n-k-1 r 0 r n-k-2 相等? 再编一次码 送过来的监督位 在接收端重新生 成的监督位

一、循环码译码的原理-求循环码的伴随式电路 定理2(定理6.1.1):设s()是r()的伴随式,令f(X=r(X)(mod xn1),则f((X的伴随式s1(=s((modg()。 证明(课本证明不好): r(☒=rn1X0-1+rn-2X02+ +『1X+r0 灯()=n1X0+rn-2X01+ rx2 +rox f(x)= [n-2X-1+「n-3X-2+.+r1X2+roX+rn1 =-rn-1X0 +X灯( +rn-1 =-rn-1(xn-1) +X灯(X) =-rnh(x)g(x)+x (a(x)g(x)+s(x)) =-rn-h(x)g(x)+x a(x)g(X)+xs(x) =(-rnh(x)+x a(x))g(x)+xs(x) s1(X)=f(X≡Xs(X(modg(X)
一、循环码译码的原理----求循环码的伴随式电路 定理2(定理6.1.1):设s(x)是r(x)的伴随式,令f(x)xr(x) (mod x n -1), 则f(x)的伴随式s1 (x)xs(x) (mod g(x))。 证明(课本证明不好): r(x) =rn-1x n-1+ rn-2x n-2 + …. + r1x +r0 xr(x)=rn-1x n + rn-2x n-1 + …. + r1x 2 +r0x f(x) = rn-2x n-1+ rn-3x n-2 + …. + r1x 2 + r0x +rn-1 =-rn-1x n + xr(x) +rn-1 =- rn-1 (xn -1) + xr(x) = - rn-1h(x)g(x) +x (a(x)g(x)+s(x)) = - rn-1h(x)g(x) +x a(x)g(x)+xs(x) = (- rn-1h(x) +x a(x))g(x) +xs(x) s1 (x)f(x) xs(x) (mod g(x))

一 、循环码译码的原理--求循环码的伴随式电路 定理2(定理6.1.1):设s(凶是r(9的伴随式,令f(x)=灯(X(mod xn-.1),则fx)的 伴随式s1()=s()(modg(). 因此,若对X循环移位,所对应的伴随式相当于在除以g(X)电路中无输入 右移一位。 推论1(推论6.1.1):设s9是r(的伴随式,令r(X)=r((modn-1) (j=0,1,n-1),则r(的伴随式s(X=s(凶(modg()。 ∀a(∈Fg[:r()=a()r((mod xn-1)的伴随式s()=a()s((modg()
一、循环码译码的原理----求循环码的伴随式电路 定理2(定理6.1.1):设s(x)是r(x)的伴随式,令f(x)xr(x) (mod xn -1), 则f(x)的 伴随式s1 (x)xs(x) (mod g(x))。 因此,若对r(x)循环移位,所对应的伴随式相当于在除以g(x)电路中无输入 右移一位。 推论1(推论6.1.1):设s(x)是r(x)的伴随式,令rj (x)x j r(x) (mod xn -1) (j=0,1,…n-1), 则ri (x)的伴随式sj (x)x js(x) (mod g(x))。 a(x)Fq [x]: rj (x)a(x)r(x) (mod xn -1)的伴随式sj (x)a(x)s(x) (mod g(x))

二、循环码的译码电路 --梅吉特译码法(只纠一个错) r(x) 计算s()电路(除以g(x) s)→ec(判别最高位是否有错) rx缓冲 c n-有错,纠正 r(X)=rn-1x-1+rn2x2+...+rx+ro->X((rn-1+1)x-1+rn2x2+...+rx+ro)=X(r(X)+x-1) ≡Xr(X)+1(m0dxn-11) 除以g() 相当于s(X)移位后加1 S(X) xs(X)+1 如果错误发生在最高位,由于接收字不是码字,所以伴随式不为0,可以通过其伴 随式与纠错后(是一个码字)的关系将其校正。 如果错误不发生在最高位,而是发生在次高位,通过将其循环移位就可以将错误图 样移到最高位,而且伴随式可通过刚求出的伴随式通过移位的方法求出
二、循环码的译码电路------梅吉特译码法(只纠一个错) 计算s(x)电路(除以g(x)) s(x)→e(x)(判别最高位是否有错) r(x)缓冲 ....... r(x) + c(x) + r(x)=rn-1x n-1+ rn-2x n-2 +…+r1x+r0 → x((rn-1+1)xn-1+ rn-2x n-2 +…+r1x+r0 )=x(r(x)+xn-1 ) xr(x)+1 (mod xn-1 -1) 除以g(x) s(x) xs(x)+1 如果错误发生在最高位,由于接收字不是码字,所以伴随式不为0,可以通过其伴 随式与纠错后(是一个码字)的关系将其校正。 如果错误不发生在最高位,而是发生在次高位,通过将其循环移位就可以将错误图 样移到最高位,而且伴随式可通过刚求出的伴随式通过移位的方法求出。 rn-1有错,纠正 相当于s(x)移位后加1
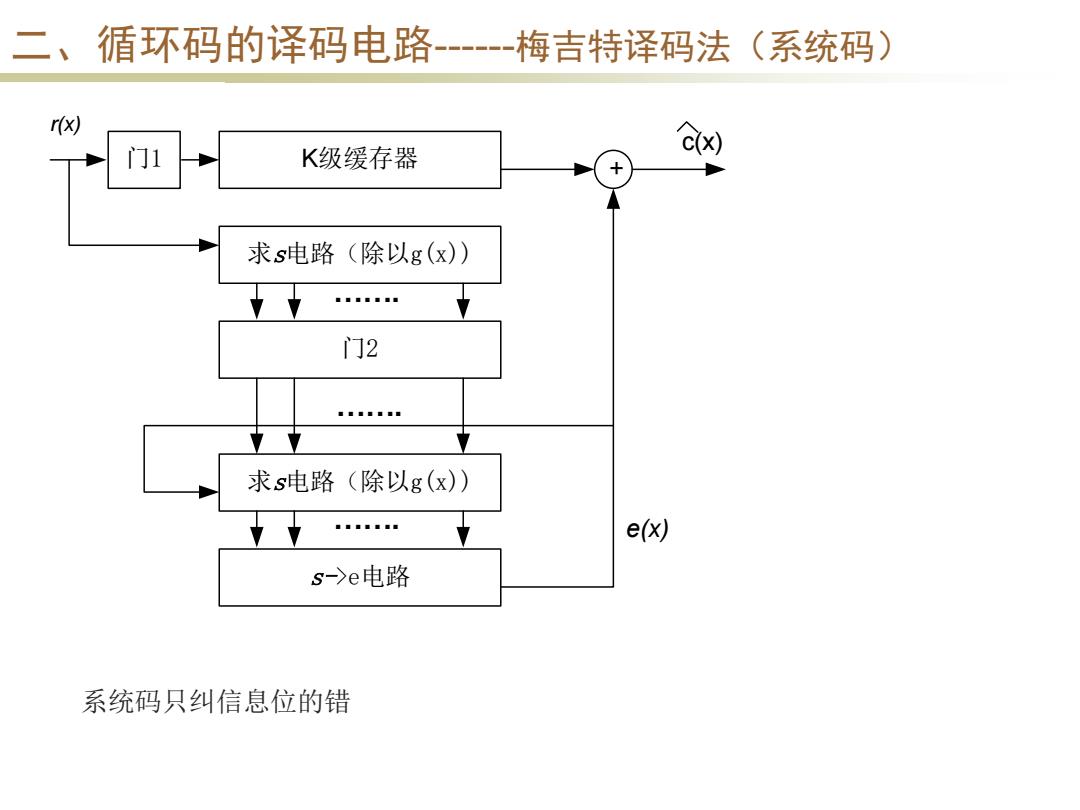
二、循环码的译码电路--梅吉特译码法(系统码) r(x) 门1 K级缓存器 ex刈 求s电路(除以g(x) nnnn■nn 门2 求s电路(除以g(x) e(x) s->e电路 系统码只纠信息位的错
二、循环码的译码电路------梅吉特译码法(系统码) K级缓存器 求s电路(除以g(x)) 求s电路(除以g(x)) 门2 门1 + ……. ……. r(x) s->e电路 ……. e(x) c(x) 系统码只纠信息位的错