
第二章代数基础 陆以勤 2005年3月
第二章 代数基础 陆以勤 2005年3月

一、整数的一些基本性质 1.基本概念 素数 合数 因数(约数) 素因数 0 公约数 最大公约数(greatest common divisor) a,b的最大公约数记为GCD(a,b)或(a,b) ■ 最小公倍数((least common multiple) a,b的最小公倍数记为LCM(a,b)或[a,b]
一、整数的一些基本性质 1. 基本概念 ◼ 素数 ◼ 合数 ◼ 因数(约数) 素因数 公约数 最大公约数(greatest common divisor) a,b的最大公约数记为GCD(a,b) 或(a,b) ◼ 最小公倍数 (least common multiple) a,b的最小公倍数记为LCM(a,b) 或 [a,b]

2.整数的初等运算及性质 加、减、乘、除 定理1。任何正整数a均可唯一地分解为素因数的积。 a=pp22.....om (p1、P2、…pn素数,「1、2、、rn为正整数) 《水浒》 天罡星:36=22×32 地煞星:72=23×32 好汉:108=22×32+23×32=22×32(1+2)=22×33
2. 整数的初等运算及性质 加、减、乘、除 定理1。任何正整数a均可唯一地分解为素因数的积。 a=p1 r1p2 r2……pn rn (p1、p2 、 ……pn素数, r1、r2、……、rn为正整数) 《水浒》 天罡星:36=2 2 × 3 2 地煞星:72=2 3 × 3 2 好汉: 108=2 2 × 3 2 + 23 × 3 2 = 22 × 3 2(1+2)= 2 2 × 3 3

3.欧几里德除法(求最大公约数) 定理2(欧几里德除法):设b是正整数,则任意大于b的正整数a 可唯一地表示为: a=qb+r0≤rb,设a=bq+r,则(a,b)=(b,r)。 解释:利用欧几里德除法求最大公约数。 例2.1.求(150,42) 150=3×42+24 42=24+18 24=18+6 18=3×6 (150,42)=(42,24)=(24,18)=(18,6)=6 求((a,b,c)=(a,b),c
3. 欧几里德除法(求最大公约数) 定理2(欧几里德除法):设b是正整数,则任意大于b的正整数a 可唯一地表示为: a=qb+r 0r b, 设a=bq+r, 则(a,b)=(b,r)。 解释:利用欧几里德除法求最大公约数。 例2.1. 求(150,42) 150=342+24 42=24+18 24=18+6 18=3 6 (150,42)=(42,24)=(24,18)=(18,6)=6 求(a,b,c)=((a,b),c)

4.欧几里德算法 定理4:给定任意a、b,(a,b)=Aa+Bb,(A、B为整数)。 解释:两个正整数的最大公约数可表示为它们的线性组合。 如何求? (150,42) 150=3×42+24 42=24+18 24=18+6 18=3×6 (150,42)=(42,24)=(24,18)=(18,6)=6 (150,42)=24-18=24-(42-24)=2×24-42 =2×(150-3×42)-42 =2×(150-3×42)-42 =2×150-7×42
4. 欧几里德算法 定理4:给定任意a、b, (a,b)=Aa+Bb, (A、B为整数)。 解释:两个正整数的最大公约数可表示为它们的线性组合。 如何求? (150,42) 150=342+24 42=24+18 24=18+6 18=3 6 (150,42)=(42,24)=(24,18)=(18,6)=6 (150,42)=24-18=24-(42-24)=2 24-42 =2 (150-3 42)-42 =2 (150-3 42)-42 = 2 150- 7 42

5.最小公倍数(1) 法1(利用定理1):把a、b分解为素因子,取不同素因子最高 次幂的积。 [198,240,360] 198=2×32×11 240=24×3 ×5 360=23×32 ×5 [198,240,360]=24×32×11×5=7920 法2. I.求两个正整数的GCM 定理5:若a、b为正整数,[a,b]=ab/(a,b)
5. 最小公倍数(1) ◼ 法1(利用定理1):把a、b分解为素因子,取不同素因子最高 次幂的积。 [198,240,360] 198=2 3 2 11 240=2 43 5 360=2 33 2 5 [198,240,360]=2 43 2115 =7920 ◼ 法2. I.求两个正整数的GCM 定理5:若a、b为正整数,[a,b]=ab/(a,b)

5.最小公倍数(2) 求:[24871,3468] I.求两个以上正整数的GCM [a,b,c]=[a,b],c] 求:[198,240,360] 6.同余和剩余类 ① 同余(余数相同):a、b、m为正整数,由欧几理德除法,a,b可 唯一地表示为: a=qim +r1 b=q2m +r2 若r=r2,则称a,b关于模m同余,记为a≡b(modm)
5. 最小公倍数(2) 求:[24871,3468] II. 求两个以上正整数的GCM [a,b,c] = [ [a,b],c] 求:[198,240,360] 6. 同余和剩余类 ① 同余(余数相同):a、b、m为正整数,由欧几理德除法,a,b可 唯一地表示为: a=q1m + r1 b=q2m + r2 若r1=r2,则称a,b关于模m同余,记为ab(mod m)

6.同余和剩余类(2) 2 模m的剩余类(同余):全体整数按模m同余的分为一类, 共有m类,称为模m的同余或剩余类,记为: 0,1,,m-1 或{0},{1},…,{m-1} 定义:{a}+b}={atb} {a}.{b}={a.b} 定理6:若a1≡b1(modm),a2=b2(modm,则 (1)a1+a2=b1+b2(modm); 同余 (2)a1.a2≡b1.b2(modm). a1 b1 a2 b2 a1+a2 b1+b2
6. 同余和剩余类(2) ② 模m的剩余类(同余):全体整数按模m同余的分为一类, 共有m类,称为模m的同余或剩余类,记为: 0, 1, ..., m −1 或{0},{1},… , {m-1} 定义:{a}+{b}={a+b} {a}.{b}={a.b} 定理6:若a1 b1 (mod m), a2 b2 (mod m), 则 (1)a1+a2 b1+b2 (mod m); (2) a1 .a2 b1 .b2 (mod m). a1 a2 b1 b2 a1+a2 b1+b2 同余
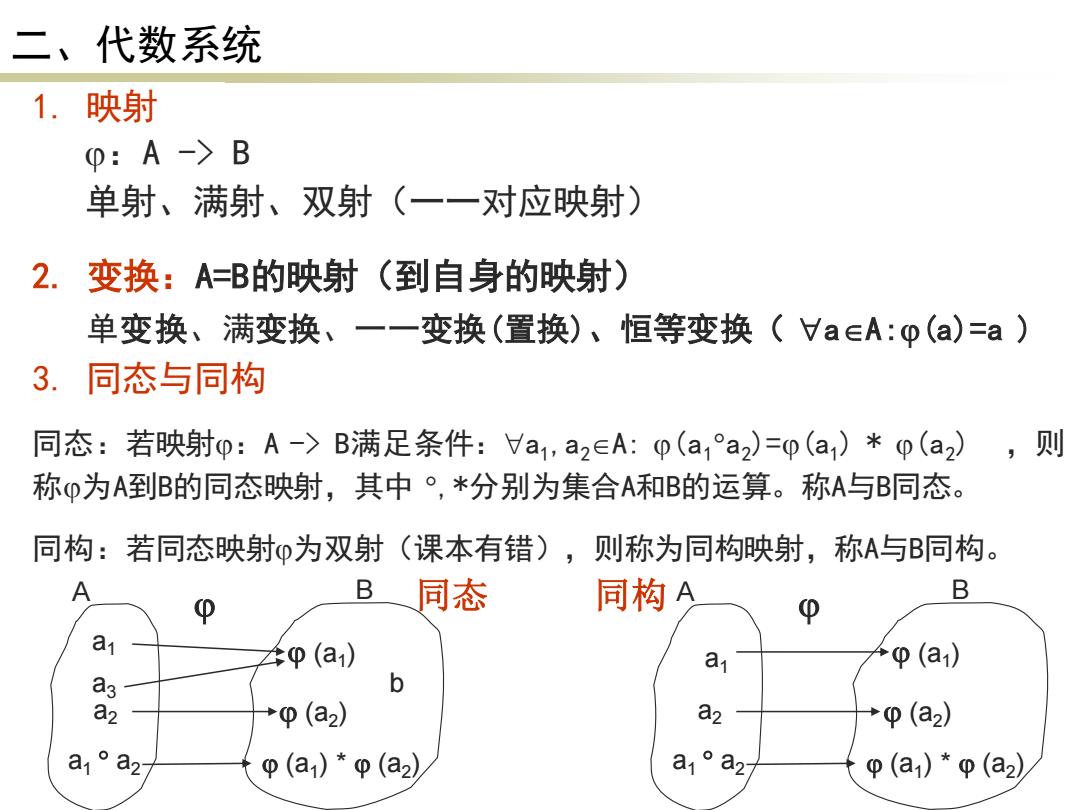
二、代数系统 1.映射 0:A->B 单射、满射、双射(一一对应映射) 2.变换:A=B的映射(到自身的映射) 单变换、满变换、一一变换(置换)、恒等变换(VaeA:p(a)=a) 3.同态与同构 同态:若映射p:A->B满足条件:a1,a2∈A:p(a1°a2)=0(a1)*p(a2),则 称0为A到B的同态映射,其中·,*分别为集合A和B的运算。称A与B同态。 同构:若同态映射0为双射(课本有错),则称为同构映射,称A与B同构。 A B同态 同构A B 81 在p(a) 4p(a) a2 +p(a2) a2 +φ(a2) a1°a27 φ(a)*p(a2) a1°a2 φ(a)*p(a2)
二、代数系统 1. 映射 :A -> B 单射、满射、双射(一一对应映射) 2. 变换:A=B的映射(到自身的映射) 单变换、满变换、一一变换(置换)、恒等变换( aA:(a)=a ) 3. 同态与同构 同态:若映射:A -> B满足条件:a1,a2A: (a1 a2)=(a1) * (a2) ,则 称为A到B的同态映射,其中 ,*分别为集合A和B的运算。称A与B同态。 同构:若同态映射为双射(课本有错),则称为同构映射,称A与B同构。 a1 a2 (a1 ) a1 a2 A B (a2 ) (a1 ) * (a2 ) a3 b a1 a2 (a1 ) a1 a2 A B (a2 ) (a1 ) * (a2 ) 同态 同构

三、群Group 只有一种运算的代数系统 1.定义:设G是非空集合,并在G定义了一种代数运算“o”,若下述公理 成立,则称G为群,记为(G,°): (1)满足封闭性:Va,beG:a°beG; (2)结合律成立:Va,b∈G:(a°b)c=a(bc); (3)存在恒等元:3eeG:Va∈G:a°e=ea=a; (4)每一元素存在逆元:Va∈G:a1∈G:aa1=a1oa=e. 群的阶:IG 有限群:IG<∞ 无限群:IG=oo 阿贝尔群、交换群:Va,beG:ab=b°a. 例:全体整数对于加法构成群,对乘法不构成群。 全体偶数对于加法构成群,对乘法不构成群。 恒等元为 全体实数R对于加法构成群,对乘法不构成群,但R-{O}对乘法构成群。)
三、群 Group 只有一种运算的代数系统 1. 定义:设G是非空集合,并在G定义了一种代数运算“” ,若下述公理 成立,则称G为群,记为(G, ): (1) 满足封闭性: a,bG:a bG; (2) 结合律成立: a,bG: (a b)c = a ( bc) ; (3) 存在恒等元: eG: a G: ae =e a =a; (4) 每一元素存在逆元: a G: a -1 G: a a -1=a-1 a=e. 群的阶:|G| 有限群: |G|< 无限群: |G|= 阿贝尔群、交换群:a,b G: a b=b a. 例:全体整数对于加法构成群,对乘法不构成群。 全体偶数对于加法构成群,对乘法不构成群。 全体实数R对于加法构成群,对乘法不构成群,但R-{0}对乘法构成群。 恒 等 元 为 0