华南理工大学：《现代编码理论与技术》课程教学资源（讲义）第三章线性分码组.doc_大学文库

《纠错码学习大纲》陆以勤第三章孩性分组码一、线性分组码 ●线性分组码[n,kd是方程HC=0T的k维解空间，H是由Fg(g=p",p为素数)中元素组成的秩为rk的 n-k×n矩阵。张成该码空间的一组基组成的k×n矩阵G称为[n,kd的生成矩阵d可由两种方法求出 ()定理4d=mW(c片 (2)定理7：若H的任意r列线性无关，并存在r+1列线性相关，则d=r+1;反之，若d=r+1,则H的任意r列线性无关，而必存在有相关的”+1列，由此可知，只要找到一个秩为-k的nk×n矩阵H或k个线性无关的n维向量（由它们可构成G)就可以生成一个线性分组码[n,内。关键是为使[n,有纠1个错误的能力，必须要d≥21+1.因此，H必须满足任意21列线性无关，并存在21+1列线性相关.对于二元码，只要H任意两列不等并且不含全0的列，这个码至少可纠一个错例如，H的列向量按1~2m1的二进制排列，任意两列线性无关，而存在线性相关的3列，因此可得 [2m.1,2m.1-m,3]的码（汉明码） ●由H的标准形式H=[QI-k]或相应的G的标准形式G=[Uk-Q门确定的线性分组码称为系统码，系统码保留了信息位并在后面加监督位 ●若把H作为生成矩阵则生成[n,kd的对偶码[n,n-k,d],G是它的监督矩阵 ●由己知码[，可对信息段和监督段进行简单的增删构造成新的码，从而使信息段和监督段的长度适合不同的需要.这种构造过程的关键问题是新码最小距离的变化.这可从监督矩阵变换后列向量的相关性的变化来研究 10 H : 例如，由H= 10 可把一个偶检验位加到原码字的最后，使[n,扩展为[什1，.对于汉明一十码[2m1,2m1-m,3】,由于d=3,H任两列线性无关同时存在线性相关的3列，而在H中，任三列线性无关（最后一位3个1相加不为0），但存在线性相关的4列（原在H中线性相关的3列加上H的最后一列)，所以Ⅲ确定了扩展汉明码[2m,2m-1-m,4]

《纠错码学习大纲》陆以勤一、线性分组码 ⚫ 线性分组码[n,k,d]是方程 HCT = 0T的 k 维解空间, H 是由 Fq (q = p m , p 为素数)中元素组成的秩为 n-k 的 n-k  n 矩阵。张成该码空间的一组基组成的 k  n 矩阵 G 称为[n, k, d]的生成矩阵. d 可由两种方法求出 (1) 定理 4: d = min ( ) [n .k,d] W c c ; (2) 定理 7: 若 H 的任意 r 列线性无关,并存在 r +1 列线性相关,则 d = r +1; 反之,若 d = r +1,则 H 的任意 r 列线性无关,而必存在有相关的 r +1 列. 由此可知, 只要找到一个秩为 n-k 的 n-k  n 矩阵 H 或 k 个线性无关的 n 维向量 ( 由它们可构成 G ) 就可以生成一个线性分组码[n,k]。关键是为使[n,k]有纠 t 个错误的能力, 必须要 d  2t+1. 因此, H 必须满足任意 2t 列线性无关,并存在 2t +1 列线性相关. 对于二元码, 只要 H 任意两列不等并且不含全 0 的列, 这个码至少可纠一个错. 例如, H 的列向量按 1 ~ 2 m-1 的二进制排列, 任意两列线性无关, 而存在线性相关的 3 列, 因此可得 [2m-1, 2m-1-m, 3]的码(汉明码). ⚫ 由 H 的标准形式 H = [Q In - k]或相应的 G 的标准形式 G = [I k -QT ]确定的线性分组码称为系统码,系统码保留了信息位并在后面加监督位. ⚫ 若把 H 作为生成矩阵则生成[n,k,d]的对偶码[n, n – k , d’], G 是它的监督矩阵. ⚫ 由已知码[n,k]可对信息段和监督段进行简单的增删构造成新的码, 从而使信息段和监督段的长度适合不同的需要. 这种构造过程的关键问题是新码最小距离的变化. 这可从监督矩阵变换后列向量的相关性的变化来研究. 例如, 由 H=             − − − + − 1 1 1 0 0 | | | |  H  可把一个偶检验位加到原码字的最后, 使[n, k]扩展为[n+1, k]. 对于汉明码[2m -1, 2 m -1-m, 3], 由于 d = 3, H 任两列线性无关同时存在线性相关的 3 列, 而在 H中, 任三列线性无关(最后一位 3 个 1 相加不为 0), 但存在线性相关的 4 列(原在 H 中线性相关的 3 列加上 H的最后一列),所以 H确定了扩展汉明码[2m , 2 m -1-m, 4]

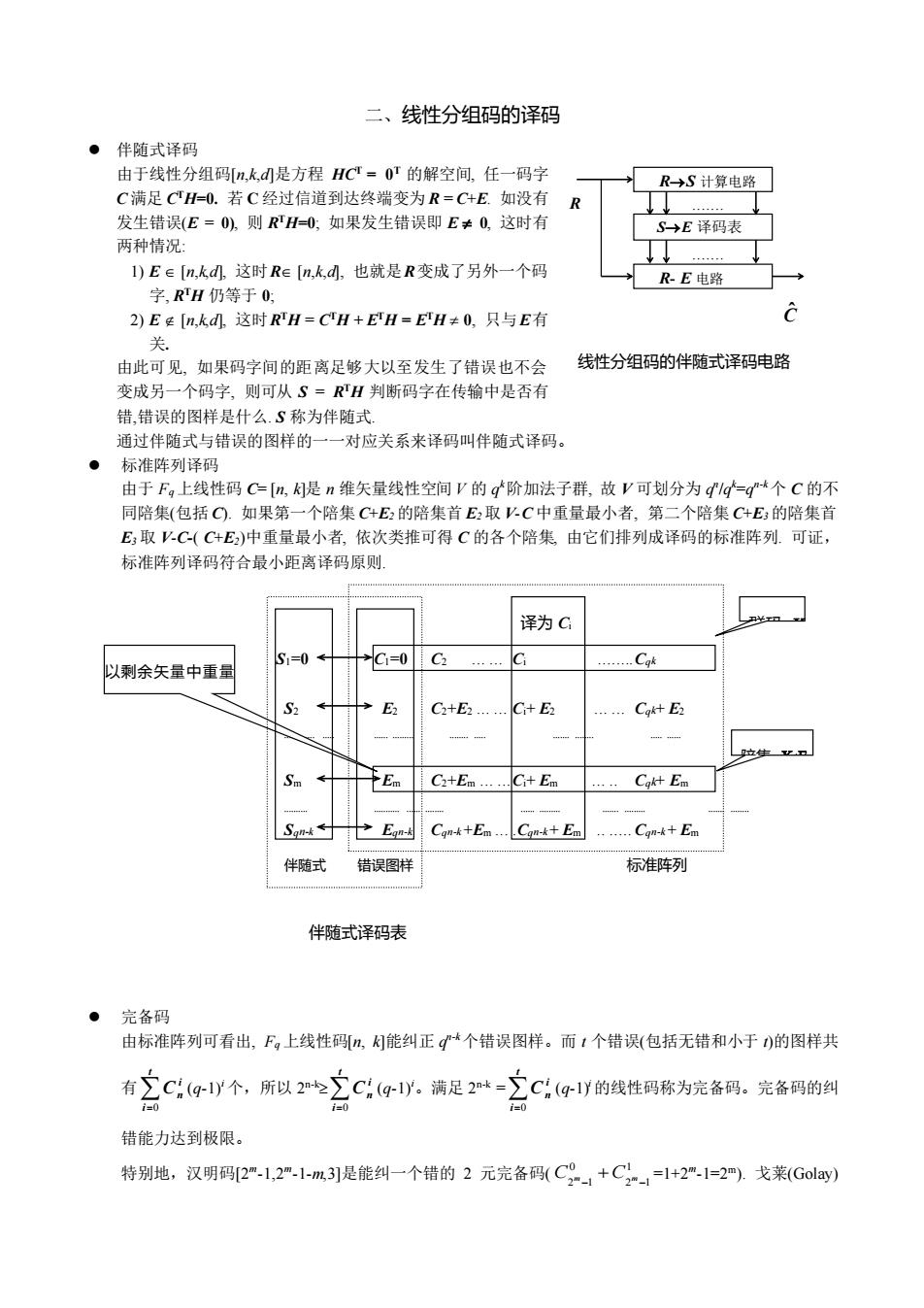
二、线性分组码的译码 ⚫ 伴随式译码由于线性分组码[n,k,d]是方程 HCT = 0T 的解空间, 任一码字 C 满足 C TH=0. 若 C 经过信道到达终端变为 R = C+E. 如没有发生错误(E = 0), 则 R TH=0; 如果发生错误即 E  0, 这时有两种情况: 1) E  [n,k,d], 这时R [n,k,d], 也就是R变成了另外一个码字, R TH 仍等于 0; 2) E  [n,k,d], 这时R TH = C TH + E TH = E TH  0, 只与E有关. 由此可见, 如果码字间的距离足够大以至发生了错误也不会变成另一个码字, 则可从 S = R TH 判断码字在传输中是否有错,错误的图样是什么. S 称为伴随式. 通过伴随式与错误的图样的一一对应关系来译码叫伴随式译码。 ⚫ 标准阵列译码由于 Fq 上线性码 C= [n, k]是 n 维矢量线性空间 V 的 q k阶加法子群, 故 V 可划分为 q n /q k =q n-k个 C 的不同陪集(包括 C). 如果第一个陪集 C+E2 的陪集首 E2 取 V-C 中重量最小者, 第二个陪集 C+E3 的陪集首 E3 取 V-C-( C+E2)中重量最小者, 依次类推可得 C 的各个陪集, 由它们排列成译码的标准阵列. 可证，标准阵列译码符合最小距离译码原则. 译为 Ci S1=0 C1=0 C2 ... ... Ci ........Cqk S2 E2 C2+E2 ... ... Ci+ E2 ... ... Cqk+ E2 ............. ..... ...... ......... ........ ..... ....... ........ ..... ...... Sm Em C2+Em ... ...Ci+ Em ... .. Cqk+ Em .......... ........... ...... ........ ...... ......... ....... ......... ....... ........ Sqn-k Eqn-k Cqn-k +Em ... .Cqn-k + Em .. ..... Cqn-k + Em 伴随式错误图样标准阵列伴随式译码表 ⚫ 完备码由标准阵列可看出, Fq 上线性码[n, k]能纠正 q n-k个错误图样。而 t 个错误(包括无错和小于 t)的图样共有 = t i i Cn 0 (q-1)i 个，所以 2 n-k = t i i Cn 0 (q-1)i。满足 2 n-k == t i i Cn 0 (q-1)i 的线性码称为完备码。完备码的纠错能力达到极限。特别地，汉明码[2m -1,2m -1-m,3]是能纠一个错的 2 元完备码( 1 2 1 0 2 −1 − C m +C m =1+2 m -1=2 m). 戈莱(Golay) R C ˆ 线性分组码的伴随式译码电路群码  陪集 + 以剩余矢量中重量最小者为陪集首 R→S 计算电路 S→E 译码表 R- E 电路 .......

华南理工大学：《现代编码理论与技术》课程教学资源（讲义）第三章 线性分码组

华南理工大学：《现代编码理论与技术》课程教学资源（讲义）第三章线性分码组