第六章循环码的泽码 循环码是线性码,因此遵循线性分组码的译码方法(图1),只是由于它们本身的循环性,在具体实施时 可以应用各种不同的方法简化。 一、循环码求伴随式S的方法 当然,循环码可以象线性码直接从S(x)=R(x)H求出,这时,需要n级寄存器.例如,对于循环汉明码 「1110100 [7,4,3引,H=0111010,gx)=x3+x+1,图2是计算S-S2S1S)的电路.但可利用循环码伴随式的下列 1101001 特性来简化电路: 1)由g(x)生成的循环码,R(x)的伴随式S()满足:S(X=R(x)=E(x)(mod g(x)(定理I)。因此,求S(x) 可用除gx)的电路实现。这样可把n级寄存器降为-k级。图3是循环汉明码[7,4,3]伴随式计算电路。 2)xR(x)(modx”-1)的伴随式是xSx)模gx)的余式。因此,若对R(x)循环移位,所对应的伴随式相当于在除 gx)电路中无输入右移一位。 RS计算电路 R(x) S→E译码表 R-E电路 c So 图1一般线性分组码的伴随式译码电路 图2用一般线性码的伴随式计算电路计算循环汉明码[7,4,3]的伴随式 R(x) 图3计算循环汉明码7,4,3]伴随式简化电路(除g(x) 二、循环码由伴随式S求错误图样E的方法 ●只有一个错误的情况 错误图样E取最高位为1,即Ex)=x-的 R>S电路 情况,这时,S()=E(x)T,S为H的第一 R(x) 列,即当S=(huhm1..h-ki)时,E取最高位为 S L,R的最高位加1得C(x)=R(x+x,这 S>E电路 时,由于R加1,循环移位后变成了最低位 加1,所以应在S的最低位加1以作校正; E)=x6 如果S≠(hh2.hm-k),则E(x)=O,R(x) 7级寄存器 ⊕+C=RXW+x6 循环检查下一位. 图4循环汉明码7,4,3]的译码电路 ●有多个错误的情况 1.突发性错误:捕错译码 捕错译码用于纠正突发性错误,分一般捕错译码和改进捕错译码. 1)一般捕错译码:1个错误全部集中在监督位 用一般捕错译码必须保证个错误全部集中在监督位,最坏的情况是【个错误均匀分布,所以一般
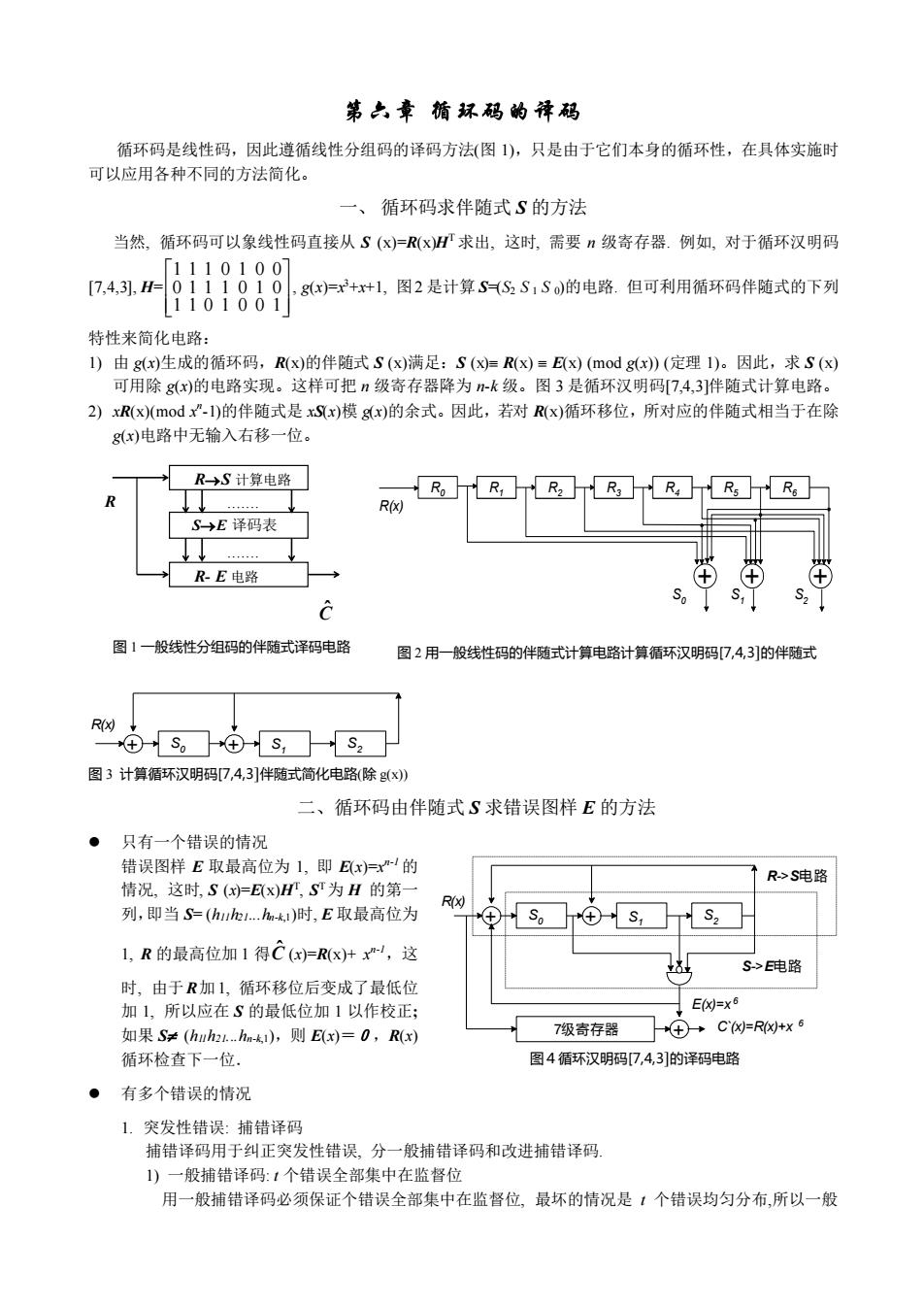
循环码是线性码,因此遵循线性分组码的译码方法(图 1),只是由于它们本身的循环性,在具体实施时 可以应用各种不同的方法简化。 一、 循环码求伴随式 S 的方法 当然, 循环码可以象线性码直接从 S (x)=R(x)HT 求出, 这时, 需要 n 级寄存器. 例如, 对于循环汉明码 [7,4,3], H= 1 1 0 1 0 0 1 0 1 1 1 0 1 0 1 1 1 0 1 0 0 , g(x)=x 3+x+1, 图2 是计算 S=(S2 S 1 S 0)的电路. 但可利用循环码伴随式的下列 特性来简化电路: 1) 由 g(x)生成的循环码,R(x)的伴随式 S (x)满足:S (x) R(x) E(x) (mod g(x)) (定理 1)。因此,求 S (x) 可用除 g(x)的电路实现。这样可把 n 级寄存器降为 n-k 级。图 3 是循环汉明码[7,4,3]伴随式计算电路。 2) xR(x)(mod x n -1)的伴随式是 xS(x)模 g(x)的余式。因此,若对 R(x)循环移位,所对应的伴随式相当于在除 g(x)电路中无输入右移一位。 R0 + R1 R2 R3 R4 R5 R6 + + R(x) S0 S1 S2 图 2 用一般线性码的伴随式计算电路计算循环汉明码[7,4,3]的伴随式 + + R(x) S0 S1 S2 图 3 计算循环汉明码[7,4,3]伴随式简化电路(除 g(x)) 二、循环码由伴随式 S 求错误图样 E 的方法 ⚫ 只有一个错误的情况 错误图样 E 取最高位为 1, 即 E(x)=x n-1 的 情况, 这时, S (x)=E(x)HT , S T为 H 的第一 列,即当 S= (h11h21...hn-k,1)时, E 取最高位为 1, R 的最高位加 1 得 C ˆ (x)=R(x)+ x n-1,这 时, 由于R加1, 循环移位后变成了最低位 加 1, 所以应在 S 的最低位加 1 以作校正; 如果 S (h11h21...hn-k,1),则 E(x)=0,R(x) 循环检查下一位. ⚫ 有多个错误的情况 1. 突发性错误: 捕错译码 捕错译码用于纠正突发性错误, 分一般捕错译码和改进捕错译码. 1) 一般捕错译码: t 个错误全部集中在监督位 用一般捕错译码必须保证个错误全部集中在监督位, 最坏的情况是 t 个错误均匀分布,所以一般 R C ˆ 图 1 一般线性分组码的伴随式译码电路 S->E电 路 + + R(x) S0 S1 S2 7级寄存器 + E(x)=x 6 R->S电 路 C`(x)=R(x)+x 6 图4循环汉明码[7,4,3]的译码电路 R→S 计算电路 S→E 译码表 R- E 电路 .......

捕错译码的先决条件是k≤M-1.如果监督位在最低位,有以下充要条件(定理3):纠1错误的F。 上的n,循环码,捕错译码过程第ⅰ个循环已把1个错误集中在最低-k位以内的充要条件是 (S(x)≤1,其中S(x)为第i个循环的伴随式.用此式可作为判断最低n-k是否有错的条件 2)改进捕错译码:1个错误大部分全部集中在监督位,而发生在信息位的j个错误图样己知为Q(x), Q2(x),,Q(x).可证,出现Q1(x)(=1,2,J》错误图样时,1w(S(xS(x)≤-(Q(x),其中S(x)为Q() 的伴随式,这可作为判断是否出现O(x)错误图样的条件 2.大数逻辑译码 1)一步大数逻辑译码 大数逻辑译码是把H作变换为Ho使H第一位的元素全为山,而其它位的元素只在某一行为1这时, 如果最高位发生错误,而其它的1个错误小于H的列数的一半,则R(x)对于H的伴随式S不为 0的数为多数,用此可判断最高位是否有错.经过循环移位可判断所有的1个错误 2)二步大数逻辑译码 二步大数逻辑译码是先应用一步大数逻辑译码的原理判断某几位是否有错,如果有错,第二步再 判断是具体的那一位
捕错译码的先决条件是 k n/t-1. 如果监督位在最低位, 有以下充要条件(定理 3): 纠 t 错误的 Fq 上的[n, k]循环码, 捕错译码过程第 i 个循环已把 t 个错误集中在最低 n-k 位以内的充要条件是 w(Si(x)) t, 其中 Si(x) 为第 i 个循环的伴随式. 用此式可作为判断最低 n-k 是否有错的条件. 2)改进捕错译码: t 个错误大部分全部集中在监督位, 而发生在信息位的 j 个错误图样已知为 Q1(x), Q2(x),..., Qj(x). 可证, 出现Ql (x) (l=1,2, ..j))错误图样时, w(S(x)-Sl(x)) t-w(Ql (x)),其中Sl(x)为Ql (x) 的伴随式, 这可作为判断是否出现 Ql (x)错误图样的条件. 2. 大数逻辑译码 1) 一步大数逻辑译码 大数逻辑译码是把H作变换为H0 使H0 第一位的元素全为1, 而其它位的元素只在某一行为1.这时, 如果最高位发生错误, 而其它的 t-1 个错误小于 H0 的列数的一半, 则 R(x)对于 H0 的伴随式 S不为 0 的数为多数, 用此可判断最高位是否有错. 经过循环移位可判断所有的 t 个错误. 2) 二步大数逻辑译码 二步大数逻辑译码是先应用一步大数逻辑译码的原理判断某几位是否有错, 如果有错, 第二步再 判断是具体的那一位