
电子种越女学 University of Electroe Scioncad TechofChina 986 Chapter 15 Numerical Strength Reduction Xiang LING National Key Lab of Science and Technology on Communications
Chapter 15 Numerical Strength Reduction Xiang LING National Key Lab of Science and Technology on Communications

Introduction /96 ■ Numerical strength reduction is a transformation techniques for reducing strength of DSP computations. This transformation relays on sub expression elimination (also referred to as substructure sharing). 2021年2月 通信抗干扰技术国家重点实验室 2
2021年2月 通信抗干扰技术国家重点实验室 2 Introduction Numerical strength reduction is a transformation techniques for reducing strength of DSP computations. This transformation relays on sub expression elimination (also referred to as substructure sharing)

Sub-expression elimination 96 Sub-expression elimination is a numerical transformation of the constant multiplications that can lead to efficient hardware in terms of area,power and speed. Sub-expression can only be performed on constant multiplications that operate on a common variable. It is essentially the process of examining the shift and add implementations of the constant multiplications and finding redundant operations. Example:a x and b x,where a=001101 and b=011011 can be performed as follows: ■ a*×=000100*×+001001*× ■ b*×=010010*×+001001*×=(001001*x)<<1+(001001*×) The term 001001 x needs to be computed only once. So,multiplications were implemented using 3 shifts and 3 adds as opposed to 5 shifts and 5 adds. 2021年2月 通信抗干扰技术国家重点实验室 3
2021年2月 通信抗干扰技术国家重点实验室 3 Sub-expression elimination Sub-expression elimination is a numerical transformation of the constant multiplications that can lead to efficient hardware in terms of area, power and speed. Sub-expression can only be performed on constant multiplications that operate on a common variable. It is essentially the process of examining the shift and add implementations of the constant multiplications and finding redundant operations. Example: a * x and b * x, where a = 001101 and b = 011011 can be performed as follows: a * x = 000100 * x + 001001 * x b * x = 010010 * x + 001001 * x = (001001 * x) << 1 +(001001 * x). The term 001001 * x needs to be computed only once. So, multiplications were implemented using 3 shifts and 3 adds as opposed to 5 shifts and 5 adds

Multiple Constant Multiplication The algorithm for MCM uses an iterative matching process that consists of the following steps: 1. Express each constant in the set using a binary format (such as signed,unsigned,2's complement representation). 2. Determine the number of bit-wise matches(nonzero bits)between all of the constants in the set. 3.Choose the best match. 4. Eliminate the redundancy from the best match.Return the remainders and the redundancy to the set of coefficients. 5.Repeat Steps 2-4 until no improvement is achieved. 2021年2月 通信抗干扰技术国家重点实验室 4
2021年2月 通信抗干扰技术国家重点实验室 4 Multiple Constant Multiplication The algorithm for MCM uses an iterative matching process that consists of the following steps: 1. Express each constant in the set using a binary format (such as signed, unsigned, 2’s complement representation). 2. Determine the number of bit-wise matches (nonzero bits) between all of the constants in the set. 3. Choose the best match. 4. Eliminate the redundancy from the best match. Return the remainders and the redundancy to the set of coefficients. 5. Repeat Steps 2-4 until no improvement is achieved

Multiple Constant /96 Multiplication Example: Constant Value Unsigned a 237 11101101 b 182 10110110 93 01011101 Binary representation of constants Constant Unsigned Constant Unsigned Rem.of a 10100000 Rem.of a 00000000 b 10110110 Rem.of b 00010110 Rem.of c 00010000 Rem.of c 00010000 Red.of a,c 01001101 Red.of a,c 01001101 Red.of Rem a,b 10100000 Updated set of constants 1st iteration Updated set of constants 2nd iteration 2021年2月 通信抗干扰技术国家重点实验室 5
2021年2月 通信抗干扰技术国家重点实验室 5 Multiple Constant Multiplication

Linear Transformations 96 A general form of linear transformation is given as: y =T*x where,T is an m by n matrix,y is length-m vector and x is a length-n vector.It can also be written as: Y=2mi=0tǒi=0n o The following steps are followed: Minimize the number of shifts and adds required to compute the products t by using the iterative matching algorithm. Formation of unique products using the sub-expression found in the 1st step. Final step involves the sharing of additions,which is common among the yi's.This step is very similar to the MCM problem. 2021年2月 通信抗干扰技术国家重点实验室 6
2021年2月 通信抗干扰技术国家重点实验室 6 Linear Transformations A general form of linear transformation is given as: y =T*x where, T is an m by n matrix, y is length-m vector and x is a length-n vector. It can also be written as: Yi=Σ n j=0 tijxj i=0,…, n The following steps are followed: Minimize the number of shifts and adds required to compute the products tijxj by using the iterative matching algorithm. Formation of unique products using the sub-expression found in the 1st step. Final step involves the sharing of additions, which is common among the yi’s. This step is very similar to the MCM problem
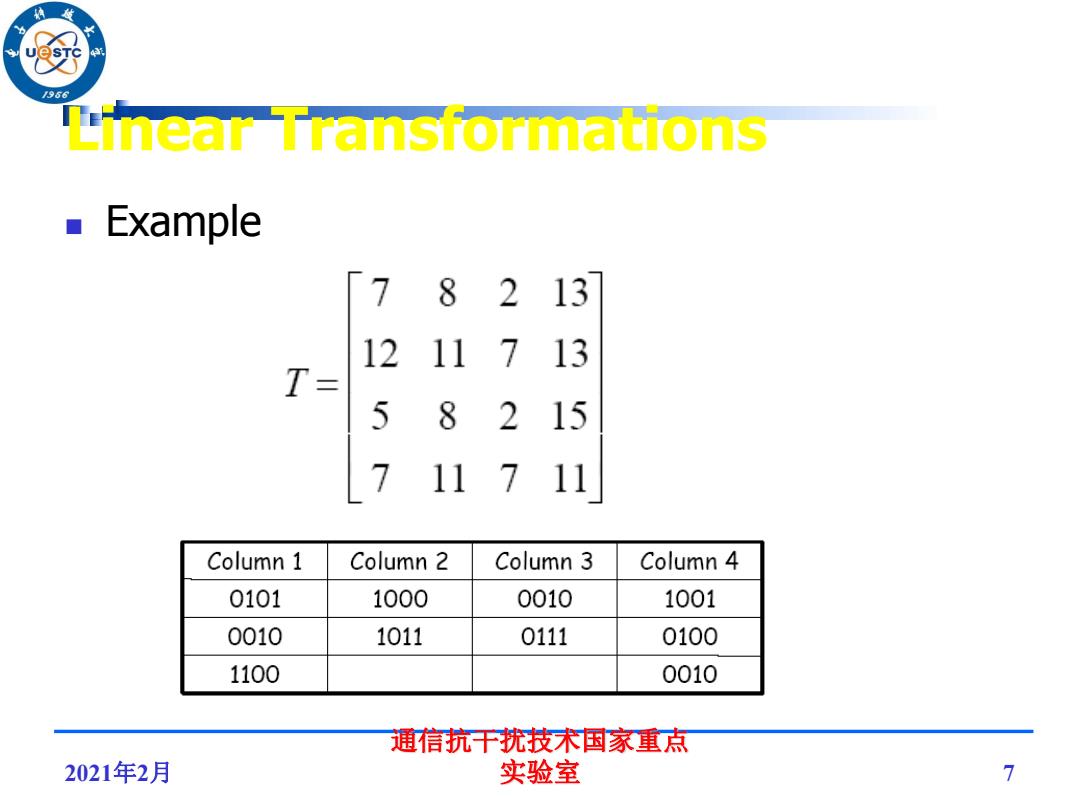
96 Linear Transformations Example 「7 82 13 12 11713 T= 5 8215 7 117 11 Column 1 Column 2 Column 3 Column 4 0101 1000 0010 1001 0010 1011 0111 0100 1100 0010 通信抗干扰技术国家重点 2021年2月 实验室 7
2021年2月 通信抗干扰技术国家重点 实验室 7 Linear Transformations Example

Linear Transformations 96 Next,the unique products are formed as shown below: p1=0101*x1,p2=0010*x1,p3=1100*x1 p4=1000*x2,p5=1011*x2,p6=0010*x3, p7=0111*x3p8=1001*x4,p9=0100*x4, p10=0010*x4 Using these products the yi's are as follows: y1=p1+p2+p4+p6+p8+p9; y2=p3+p5+p7+p8+p9; y3=p1+p4+p6+p8+p9+p10; y4=p1+p2+p5+p7+p8+p10; 2021年2月 通信抗干扰技术国家重点实验室 8
2021年2月 通信抗干扰技术国家重点实验室 8 Linear Transformations Next, the unique products are formed as shown below: p1 = 0101*x1, p2 = 0010*x1, p3 = 1100*x1 p4 = 1000*x2, p5 = 1011*x2, p6 = 0010*x3, p7 = 0111*x3 p8 = 1001*x4, p9 = 0100*x4, p10=0010*x4 Using these products the yi’s are as follows: y1 = p1 + p2 + p4 + p6 + p8 + p9; y2 = p3 + p5 + p7 + p8 + p9; y3 = p1 + p4 + p6 + p8 + p9 + p10; y4 = p1 + p2 + p5 + p7 + p8 + p10;

Linear Transformations /986 Applying iterative matching algorithm to reduce the number of additions required for yi's we get: y1=p2+(p1+p4+p6+p8+p9): y2=p3+p9+(p5+p7+p8)i y3=p10+(p1+p4+p6+p8+p9): y4=p1+p2+p10+(p5+p7+p8)i The total number of additions are reduced from 35to20. 2021年2月 通信抗干扰技术国家重点实验室 9
2021年2月 通信抗干扰技术国家重点实验室 9 Linear Transformations Applying iterative matching algorithm to reduce the number of additions required for yi’s we get: y1 = p2 + (p1 + p4 + p6 + p8 + p9); y2 = p3 + p9 + (p5 + p7 + p8); y3 = p10 + (p1 + p4 + p6 + p8 + p9); y4 = p1 + p2 + p10 + (p5 + p7 + p8); The total number of additions are reduced from 35 to 20

Polynomial Evaluation /96 Evaluating the polynomial: x13+x7+x4+x2+X Without considering the redundancies this polynomial evaluation requires 22 multiplications. Examining the exponents and considering their binary representations: 1=0001,2=0010,4=0100,7=0111,13=1101. x7 can be considered as x4 X x2 Xx.Applying sub-expression sharing to the exponents the polynomial can be evaluated as follows: x8×(x4×x)+x2×(x4×X)+x4+X2+X The terms x2,x4 and x8 each require one multiplication as shown below: X2=X×X,X4=X2×X2,8=x4×X4 Thus,we require 6 instead of 22 multiplications. 2021年2月 通信抗干扰技术国家重点实验室 10
2021年2月 通信抗干扰技术国家重点实验室 10 Polynomial Evaluation Evaluating the polynomial: x 13 + x7 + x4 + x2 + x Without considering the redundancies this polynomial evaluation requires 22 multiplications. Examining the exponents and considering their binary representations: 1 = 0001, 2 = 0010, 4 = 0100, 7 = 0111, 13 = 1101. x7 can be considered as x4 × x 2 × x. Applying sub-expression sharing to the exponents the polynomial can be evaluated as follows: x 8 × (x4 × x) + x2 × (x4 × x) + x4 + x2 + x The terms x2, x4 and x8 each require one multiplication as shown below: x 2 = x × x, x4 = x2 × x 2 , x8 = x4 × x 4 Thus, we require 6 instead of 22 multiplications