
电子料做女学 University of Electroale Science and Technelery of China /986 Chapter 9 Algorithmic strength reduction in filters and transforms Dr.Ling National Key Lab of Science and Technology on Communications
Chapter 9 Algorithmic strength reduction in filters and transforms Dr. Ling National Key Lab of Science and Technology on Communications

9.1 Introduction /96 target Algorithmic strength reduction in parallel FIR filters,discrete cosine transforms. Strength reduction leads to a reduction in hardware complexity by exploiting substructure sharing; This transformation can lead to reduction in silicon area or power consumption in a VLSI implementation or iteration period in a programmable DSP implementation. 2021年2月 2
2021年2月 2 9.1 Introduction target Algorithmic strength reduction in parallel FIR filters, discrete cosine transforms. Strength reduction leads to a reduction in hardware complexity by exploiting substructure sharing; This transformation can lead to reduction in silicon area or power consumption in a VLSI implementation or iteration period in a programmable DSP implementation

96 Parallel FIR Filters Formulation of Parallel FIR Filter Using Polyphase Decomposition design Fast FIR Filter Algorithms Discrete Cosine Transform and Inverse DCT Algorithm-Architecture Transformation Decimation-in-Frequency design Fast DCT for 2M-point DCT 2021年2月 3
2021年2月 3 Parallel FIR Filters Formulation of Parallel FIR Filter Using Polyphase Decomposition design Fast FIR Filter Algorithms Discrete Cosine Transform and Inverse DCT Algorithm-Architecture Transformation Decimation-in-Frequency design Fast DCT for 2M-point DCT

966 Fourier transform F(w)=Ff(t)]=f(t)e-iut dt. Laplac transform F)=Ef}=人feet Z transform Z({xn})=X(z)=∑x(njz-m n=-00 2021年2月 4
2021年2月 4 Fourier transform Laplac transform Z transform
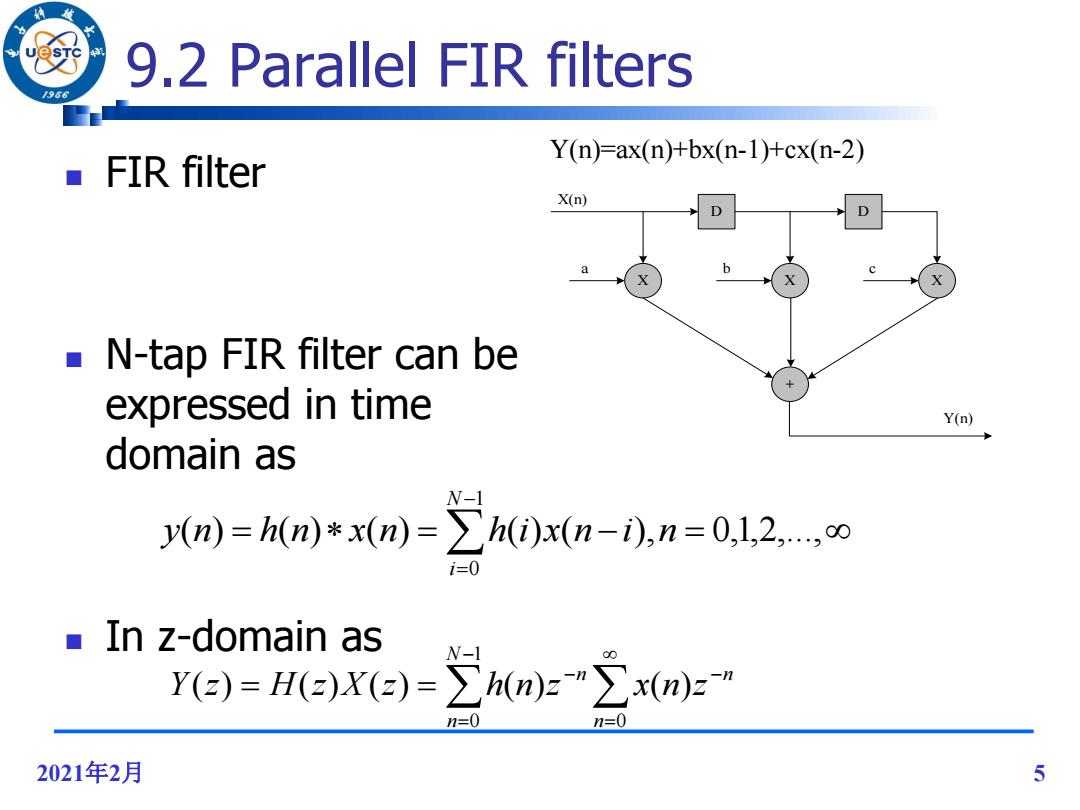
9,2 Parallel FIR filters /96 Y(n)=ax(n)+bx(n-1)+cx(n-2) FIR filter X(n) D b N-tap FIR filter can be expressed in time Y(n) domain as N-1 y(n))=h(n)*x(n)=∑h()x(n-i),n=0,12,,o i=0 In z-domain as N-I Y(e)=lH(a)X(2)=∑h(n)z"∑x(n)z n=0 n=0 2021年2月 5
2021年2月 5 9.2 Parallel FIR filters FIR filter N-tap FIR filter can be expressed in time domain as In z-domain as Y(n)=ax(n)+bx(n-1)+cx(n-2) D D X X X + a b c Y(n) X(n) 1 0 ( ) ( ) ( ) ( ) ( ), 0,1,2,..., N i y n h n x n h i x n i n 0 1 0 ( ) ( ) ( ) ( ) ( ) n n N n n Y z H z X z h n z x n z

9.2.1 Formulation of Parallel FIR using Polyphase Decomposition The input sequence can be decomposed into even-numbered part and odd-numbered part X(2)=0+x21+x222+X323+424+… =(x0+X2z2+X424+.)+z(x1+X322+Xz4+.) =X(z2)+zX(z2) similarly H(z)=H(z2)+z1H1(z2) 2021年2月 6
The input sequence can be decomposed into even-numbered part and odd-numbered part similarly 2021年2月 6 9.2.1 Formulation of Parallel FIR using Polyphase Decomposition ( ) ( ) ( ...) ( ...) ( ) ... 2 1 2 1 0 4 5 2 1 3 4 1 4 2 0 2 4 4 3 3 2 2 1 0 1 X z z X z x x z x z z x x z x z X z x x z x z x z x z ( ) ( ) ( ) 2 1 2 1 0 H z H z z H z

/96 Y(z)=Y(z2)+z1Y(z2) =(X(z2)+z1X(22)H(z2)+z1H(z2) =X(z2)H(z2)+z(X(z2)H1(z2)+X(z2)H(z2) +z2X(22)H(z2) Y(z2)=X(z2)H(z2)+z2X1(z2)H1(z2) Y(z2)=X(z2)H1(z2)+X(z2)H(z2) 2021年2月 7
2021年2月 7 2 1 2 0 1 2 1 2 2 1 2 0 1 0 1 2 2 1 2 2 2 2 0 0 0 1 1 0 2 2 2 1 1 ( ) ( ) ( ) ( ( ) ( ))( ( ) ( )) ( ) ( ) ( ( ) ( ) ( ) ( )) ( ) ( ) Y z Y z z Y z X z z X z H z z H z X z H z z X z H z X z H z z X z H z ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 0 2 1 2 1 2 0 2 1 2 1 2 1 2 2 0 2 0 2 0 Y z X z H z X z H z Y z X z H z z X z H z
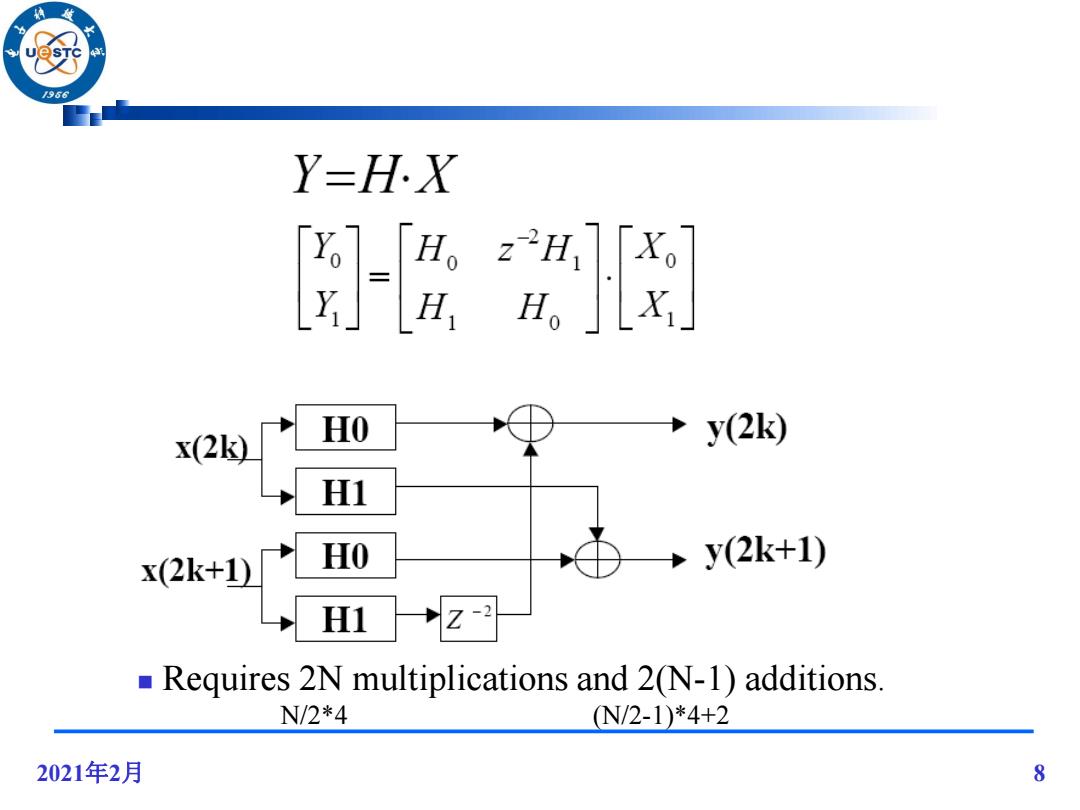
/966 Y-H.X [[医图 H, x(2k) HO y(2k) H1 x(2k+1) HO +y(2k+1) H1 z-2 Requires 2N multiplications and 2(N-1)additions. N/2*4 (N/2-1)*4+2 2021年2月 8
2021年2月 8 Requires 2N multiplications and 2(N-1) additions. N/2*4 (N/2-1)*4+2

/966 3-phase polyphase decomposition X(z)=X(z3)+z1X1(z3)+z2X2(z3) H(2)=H(2)+zH()+zH2() 2021年2月 9
3-phase polyphase decomposition 2021年2月 9 ( ) ( ) ( ) ( ) 3 2 3 2 1 3 1 0 X z X z z X z z X z ( ) ( ) ( ) ( ) 3 2 3 2 1 3 1 0 H z H z z H z z H z

Y(2)=Y(z3)+z1Y(z3)+z2Y(z3) =(X(z3)+zX(z3)+z2X2(z3)H(z3)+zH1(z3)+z2H2(z3) =X(z3)H(z3)+z(X(z3)H1(z3)+X(z3)H(23) +z2(X1(z3)H1(z3)+X2(z3)H(z3)+X(z3)H2(z3) +z3(X(z3)H2(z3)+X(z3)H1(z3)+z4X2(z3)H2(z3) Y(z3)=Xo(z3)H(z3)+z3X(z3)H2(z3)+z3X(z3)H(z3) Y(z3)=X(z3)H(z3)+X(z3)H(z3)+zX2(z3)H2(z) Y,(z3)=X(z3)H2(z3)+X2(23)H(z3)+X(z3)H1(z3) 2021年2月 10
2021年2月 10 ( ( ) ( ) ( ) ( )) ( ) ( ) ( ( ) ( ) ( ) ( ) ( ) ( )) ( ) ( ) ( ( ) ( ) ( ) ( )) ( ( ) ( ) ( ))( ( ) ( ) ( )) ( ) ( ) ( ) ( ) 3 2 3 2 3 4 1 3 2 3 2 3 1 3 3 2 3 0 3 0 3 2 3 1 3 1 2 3 0 3 1 3 1 3 0 3 1 0 3 0 3 2 3 2 1 3 1 0 3 2 3 2 1 3 1 0 3 2 3 2 1 3 1 0 z X z H z X z H z z X z H z z X z H z X z H z X z H z X z H z z X z H z X z H z X z z X z z X z H z z H z z H z Y z Y z z Y z z Y z 3 3 3 3 3 3 3 3 3 0 0 0 1 2 2 1 3 3 3 3 3 3 3 3 1 0 1 1 0 2 2 3 3 3 3 3 3 3 2 0 2 2 0 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Y z X z H z z X z H z z X z H z Y z X z H z X z H z z X z H z Y z X z H z X z H z X z H z