
电子料做女学 University of Electroe Scioncad TechofChina 986 Chapter 2 Iteration Bound Dr.Ling National Key Lab of Science and Technology on Communication
Chapter 2 Iteration Bound Dr. Ling National Key Lab of Science and Technology on Communication

2.1 Introduction /96 What is the maximum sample,operation frequency? The iteration bound is a characteristic of the representation of an algorithm in the form of a data flow graph(DFG); Different representation of the same algorithm may lead to different iteration bounds. It is not possible to achieve an iteration period less than the iteration bound even when infinite processors are available. 2021年2月 2
2021年2月 2 2.1 Introduction What is the maximum sample, operation frequency? The iteration bound is a characteristic of the representation of an algorithm in the form of a data flow graph (DFG); Different representation of the same algorithm may lead to different iteration bounds. It is not possible to achieve an iteration period less than the iteration bound even when infinite processors are available
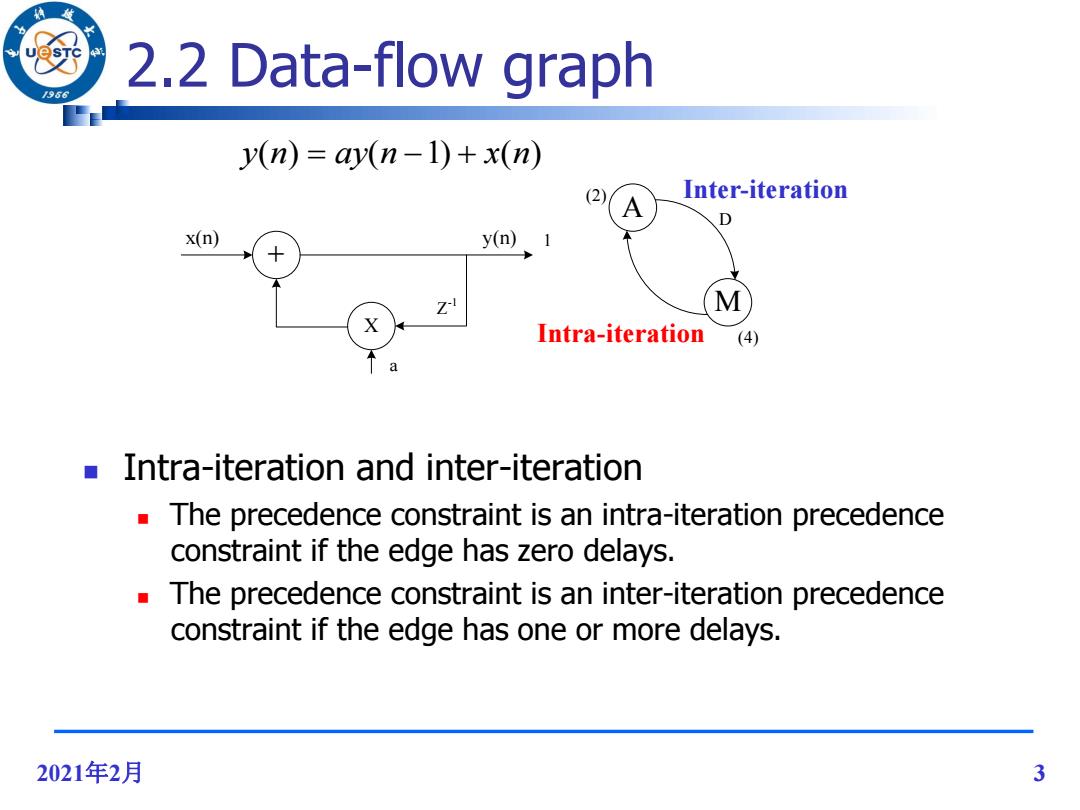
2.2 Data-flow graph 966 y(n)=ay(n-1)+x(n) (2) Inter-iteration A D x(n) y(n).1 M Intra-iteration (4) Intra-iteration and inter-iteration The precedence constraint is an intra-iteration precedence constraint if the edge has zero delays. The precedence constraint is an inter-iteration precedence constraint if the edge has one or more delays. 2021年2月 3
2021年2月 3 2.2 Data-flow graph y(n) ay(n 1) x(n) X + x(n) y(n) a Z-1 A M D 1 (4) (2) Intra-iteration and inter-iteration The precedence constraint is an intra-iteration precedence constraint if the edge has zero delays. The precedence constraint is an inter-iteration precedence constraint if the edge has one or more delays. Intra-iteration Inter-iteration
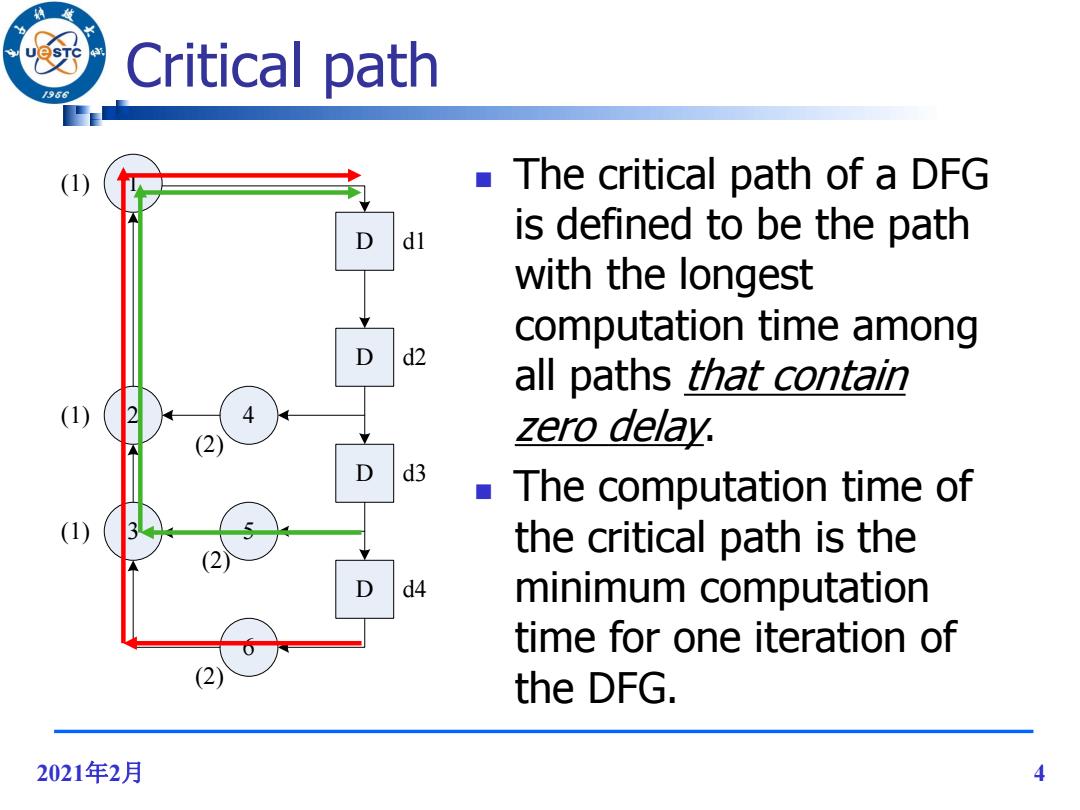
Critical path /96 The critical path of a DFG is defined to be the path with the longest computation time among d2 all paths that contain 4 zero delay. d3 The computation time of the critical path is the d4 minimum computation time for one iteration of (2 the DFG. 2021年2月 4
2021年2月 4 Critical path D 1 D D D 3 2 4 5 6 (1) (1) (2) (2) (2) (1) d1 d4 d3 d2 The critical path of a DFG is defined to be the path with the longest computation time among all paths that contain zero delay. The computation time of the critical path is the minimum computation time for one iteration of the DFG
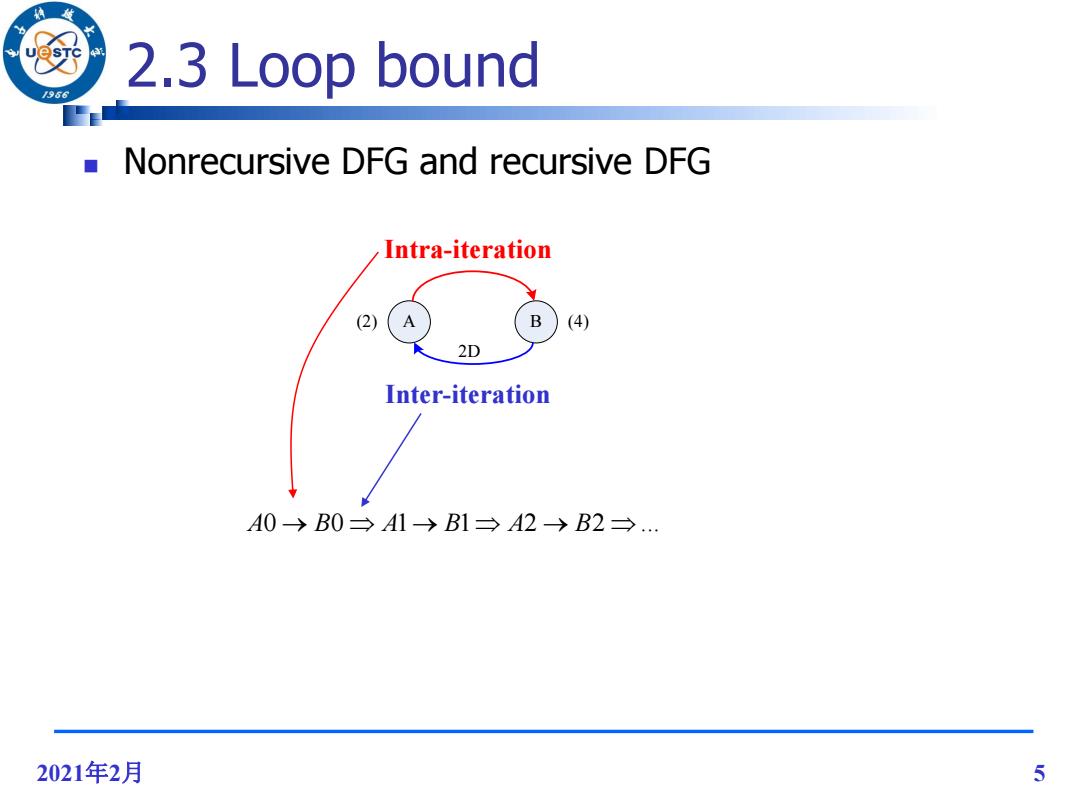
2.3 Loop bound 966 Nonrecursive DFG and recursive DFG Intra-iteration (2) (4) 2D Inter-iteration A0→B0→A1→B1→A2→B2→.. 2021年2月 5
2021年2月 5 2.3 Loop bound Nonrecursive DFG and recursive DFG (2) A B (4) 2D Intra-iteration Inter-iteration A B A B A B 0 0 1 1 2 2 ...
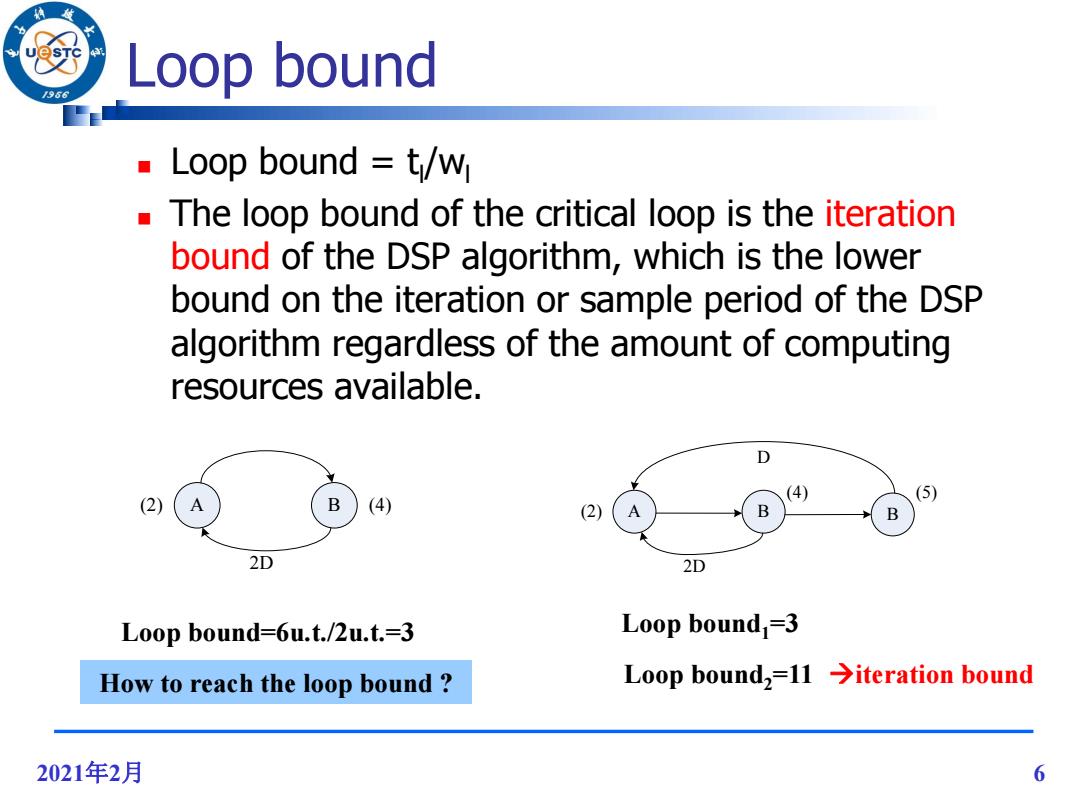
Loop bound /96 Loop bound t/w The loop bound of the critical loop is the iteration bound of the DSP algorithm,which is the lower bound on the iteration or sample period of the DSP algorithm regardless of the amount of computing resources available. D (4) (5) B (4) 2 B B 2D 2D Loop bound=6u.t./2u.t.=3 Loop bound =3 How to reach the loop bound Loop bound,=11 >iteration bound 2021年2月 6
2021年2月 6 Loop bound Loop bound = tl /wl The loop bound of the critical loop is the iteration bound of the DSP algorithm, which is the lower bound on the iteration or sample period of the DSP algorithm regardless of the amount of computing resources available. (2) A B (4) 2D B (5) D (2) A B (4) 2D Loop bound=6u.t./2u.t.=3 How to reach the loop bound ? Loop bound1=3 Loop bound2=11 iteration bound

2.3 Iteration bound 956 .n How to calculate the iteration bound? Finding all loops.>boring!!! Longest path matrix algorithm (LPM) Minimum cycle mean algorithm (MCM) Negative cycle detection algorithm 2021年2月 7
2021年2月 7 2.3 Iteration bound How to calculate the iteration bound? Finding all loops. boring!!! Longest path matrix algorithm (LPM) Minimum cycle mean algorithm (MCM) Negative cycle detection algorithm l l l L w t T max

2.4.1LPM /96 In the longest path matrix algorithm(LPM),series of matrices is constructed,the iteration bound is found by examining the diagonal elements of the matrices. L(m),m=1,2,..,d,are constructed such that value of the element I(m)is the longest computation time of all paths from delay element d to delay element d;that pass through exactly m-1 delays. If no such path exists,the I(m=-1. m Delay=m-1 (m) 72 1(m) Lm)= Longest Computation time 14 ad From i to j 2021年2月 8
2021年2月 8 2.4.1 LPM In the longest path matrix algorithm (LPM), series of matrices is constructed, the iteration bound is found by examining the diagonal elements of the matrices. L (m), m=1,2,..,d, are constructed such that value of the element l (m) i,j is the longest computation time of all paths from delay element di to delay element dj that pass through exactly m-1 delays. If no such path exists, the l(m) i,j=-1. ( ) ( ) ( ) 11 12 1 ( ) ( ) ( ) ( ) 21 22 2 ( ) ( ) ( ) 1 2 ... ... ... ... m m m d m m m m d m m m d d dd l l l l l l L l l l Delay=m-1 From i to j Longest Computation time
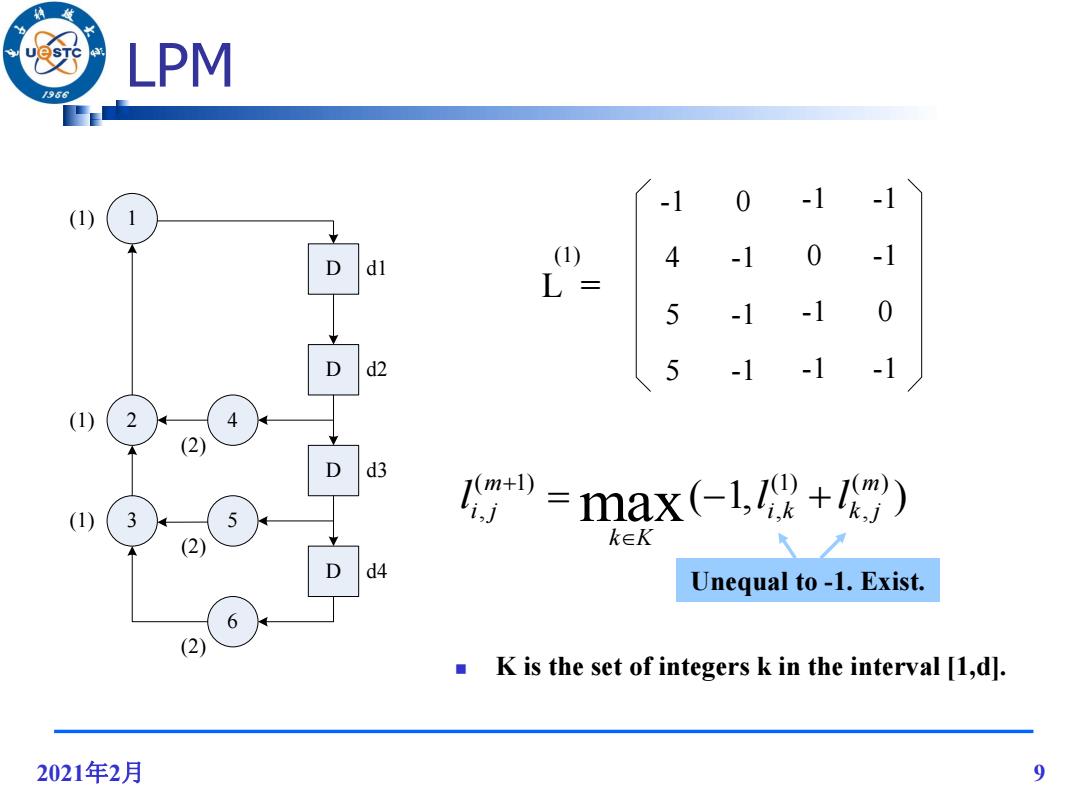
LPM 966 0 -1 -1 1) (1) 4 -1 0 -1 d L 5 -1 -1 0 d2 5 -1 -1 -1 (1) 4 (2) D d3 (1) 3 5 w+w=max-1,l供+1w) (2) k∈K d4 Unequal to -1.Exist. 6 (2) K is the set of integers k in the interval [1,d]. 2021年2月 9
2021年2月 9 LPM -1 0 -1 -1 4 -1 0 -1 5 -1 -1 -1 5 -1 -1 0 L = (1) ( 1, ) ( ) , (1) , ( 1) , max m i k k j k K m i j l l l K is the set of integers k in the interval [1,d]. D 1 D D D 3 2 4 5 6 (1) (1) (2) (2) (2) (1) d1 d4 d3 d2 Unequal to -1. Exist
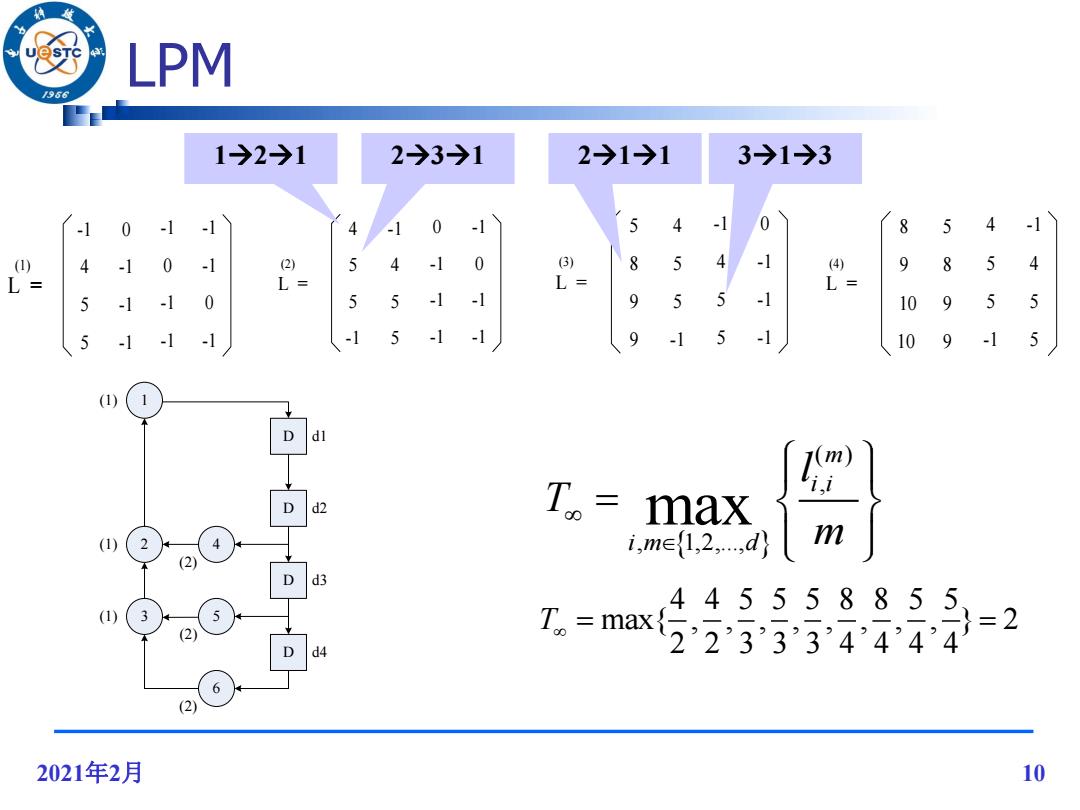
★ LPM /966 1→2→1 2→3→1 2→1→1 3→1→3 -1 0 -1 -1 4 0 5 4 -1 0 8 5 4 -1 (1) 4 -1 0 -1 (2) 5 4 -1 0 (3) 8 5 4 -1 (4) 9 8 5 4 L= L= L= L= 5 -1 -1 0 5 5 -1 -1 9 5 5 -1 10 9 5 5 5 -1 -1 -1 -1 5 -1 -1 9 -1 -1 10 9 -1 5 (1) 7.-max 2 4 i,me{1,2,…,d m (2) d3 (1) 44555885,5=2 (2) d4 T.=ma{223334444 6 (2) 2021年2月 10
2021年2月 10 LPM 4 -1 0 -1 5 4 -1 0 -1 5 -1 -1 5 5 -1 -1 L = (2) 5 4 -1 0 8 5 4 -1 9 -1 5 -1 9 5 5 -1 L = (3) 4 4 5 5 5 8 8 5 5 max{ , , , , , , , , } 2 2 2 3 3 3 4 4 4 4 T 8 5 4 -1 9 8 5 4 10 9 -1 5 10 9 5 5 L = (4) ( ) , , 1,2,..., max m i i i m d l T m 121 231 313 D 1 D D D 3 2 4 5 6 (1) (1) (2) (2) (2) (1) d1 d4 d3 d2 211 -1 0 -1 -1 4 -1 0 -1 5 -1 -1 -1 5 -1 -1 0 L = (1)