
电子料做女学 University of Electroe Scioncad TechofChina /986 Chapter 13 Bit-Level Arithmetic Architectures Xiang LING National Key Lab of Science and Technology on Communications
Chapter 13 Bit-Level Arithmetic Architectures Xiang LING National Key Lab of Science and Technology on Communications

13.1 Introduction /956 Three implementation styles ■bit parallel bit serial ■digit serial The major emphasis is on architecture design methodologies for mapping algorithms to arithmetic architecture at bit-level. 2021年2月 2
13.1 Introduction Three implementation styles bit parallel bit serial digit serial The major emphasis is on architecture design methodologies for mapping algorithms to arithmetic architecture at bit-level. 2021年2月 2

Number representation /96 A W-bit fixed point two's complement number A is represented as A=aw-1.aw-2...a1ao where the bits ai,0≤i≤W-l,are either0or1, and the MSB is the sign bit. The value of this number is in the range of [-1,1-2-W+1]and is given by A=-aw-1+∑aw-1-i2 example: 如 1000=[-1]cmp ■ 0111=-0+0.5+0.25+0.125=[0.875]cmp=1-23 ,0101=-0+0.5+0.125=[0.625]cmp 2021年2月 3
Number representation A W-bit fixed point two’s complement number A is represented as : A=aw-1 .aw-2…a1a0 where the bits ai , 0 ≤ i ≤ W-1, are either 0 or 1, and the MSB is the sign bit. The value of this number is in the range of [-1, 1–2 -W+1] and is given by : A = - aw-1 + Σaw-1-i2 -i example: 1000=[-1]cmp 0111=-0+0.5+0.25+0.125=[0.875]cmp=1-2 -3 0101=-0+0.5+0.125=[0.625]cmp 2021年2月 3

/966 For bit-serial implementations,constant word length multipliers are considered.For a WXW bit multiplication the W most-significant bits of the (2W-1)-bit product are retained. 2021年2月 4
For bit-serial implementations, constant word length multipliers are considered. For a W×W bit multiplication the W most-significant bits of the (2W-1)-bit product are retained. 2021年2月 4

13.2 Parallel Multipliers 96 Multiply A=aw-1.aw-2...a1.o=-w1aw-1-i2i B=bw-1.bw2bo=-bb Their product is given by 2T-2 P=-P2w-2+gP2w-2-2 In constant word length multiplication,W-1 lower order bits in the product P are ignored and the Product is denoted r-1 X=-Xw-1+三×w-12-1 2021年2月 5
13.2 Parallel Multipliers Multiply Their product is given by : In constant word length multiplication, W–1 lower order bits in the product P are ignored and the Product is denoted 2021年2月 5

/96 13.2.1 Parallel Multiplication with Sign Extension Using Horner's rule,multiplication of A and B can be written as P=A×(-bw1+∑bw-12-) =-A.bw-1+[A.bw-2+[A.bw-3t[.+[A.b1+Abo21]2-1]]2-1]2-1 where 2-1 denotes scaling operation. 2021年2月 6
13.2.1 Parallel Multiplication with Sign Extension Using Horner’s rule, multiplication of A and B can be written as where 2-1 denotes scaling operation. 2021年2月 6

/966 In 2's complement,negating a number is equivalent to taking its 1's complement and adding 1 to LSB as shown below: -A=m1-ga-2 =a-+0-a-- =a.-1+1-a-1-)2-1+2r1 =-1-a.-)+0-a.1-)2+2 W-1 =-āw-1+∑aw-1-2-i+2-W+1 取反加一 i=l Example: ■ 0101=>1010+1=1011=-1+0.25+0.125=[-0.625]cmp 7
In 2’s complement, negating a number is equivalent to taking its 1’s complement and adding 1 to LSB as shown below: Example: 0101 => 1010+1=1011=-1+0.25+0.125=[-0.625]cmp 7 取反加一

/966 w-1 -A= -āw-1+∑aw-1-2-i+2-W+1 i=1 -A×b3 -a3bg+a2bg2-1+a1bg2-2+a0b32-3+b32-3 Tabular form of bit-level array multiplication a3 a2 aj ao b3 b2 b1 bo Ca3bo 0 a2bo a1bo aobo ≤a3b a2b1 a1b1 aobi 二a3b2 a2b2 a162 aob2 -a3b3 a2b3 a1b3 aob3 b3 Pe Ps P4 P3 P2 P1 Po The additions cannot be carried out directly due to terms having negative weight.Sign extension is used to solve this problem
Tabular form of bit-level array multiplication 2021年2月 8 -A The additions cannot be carried out directly due to terms having negative weight. Sign extension is used to solve this problem

/966 For example, A-a3+a22-1+a122+a02-3 =-a32+a3+a22-1+a12-2+a02-3 =-a322+a32+a3+a22-1+a12-2+a2-3 a3- a2 a1 ao 3. b2 b1、 bo a3bo ←a3b0 a2bo aibo aobo a3b1 a2b1 ajbi aobi pp ←pp3 pp pp ypo a3b2 a2b2 a1b2 aob2 p ←ppi pp吃 poi ppa a3b3 a2b3 a1b3 aob3 U3 I3. C2 t1 To 2021年2月 9
For example, 2021年2月 9
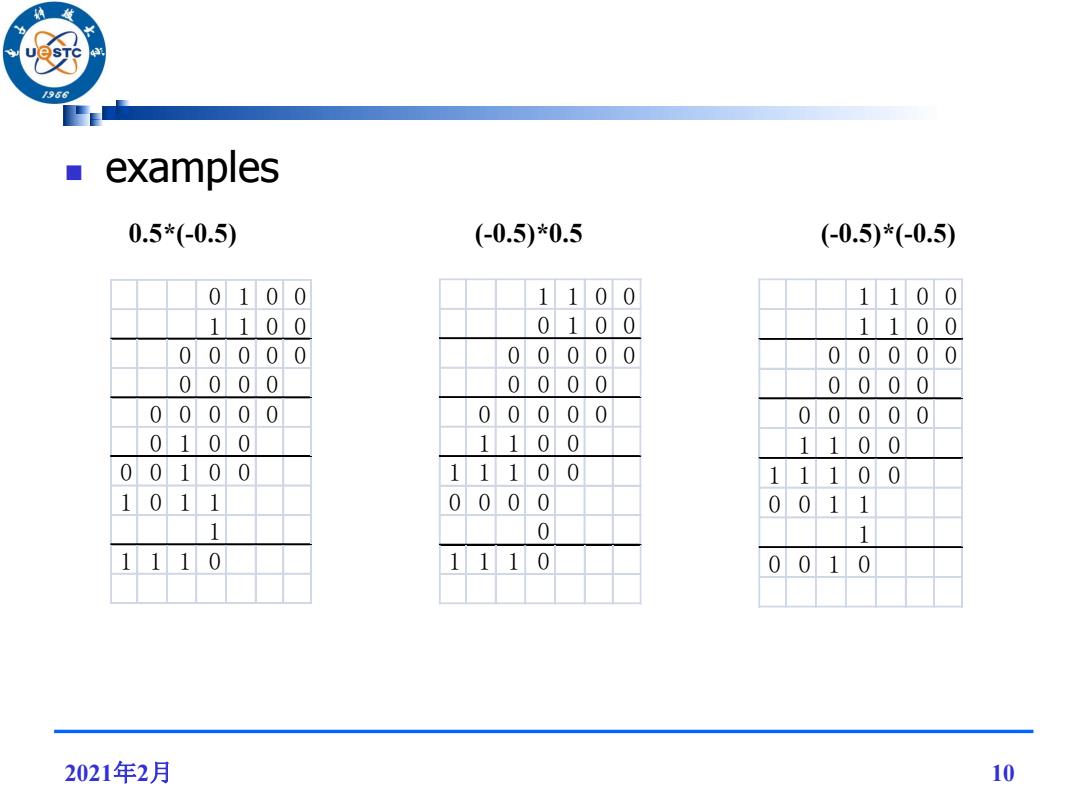
女 /966 examples 0.5*(-0.5) (-0.5)*0.5 (-0.5)*(-0.5) 0100 1 100 1100 1100 0100 1100 00000 00000 00000 0000 0000 0000 00000 00000 00000 0100 1100 1100 00100 11100 11100 1011 0000 0011 1 0 1 1110 1110 0010 2021年2月 10
examples 2021年2月 10 0.5*(-0.5) (-0.5)*0.5 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 (-0.5)*(-0.5) 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 1 1 1 0 0 1 0