
第十三章Turboi码 陆以勤
第十三章 Turbo码 陆以勤
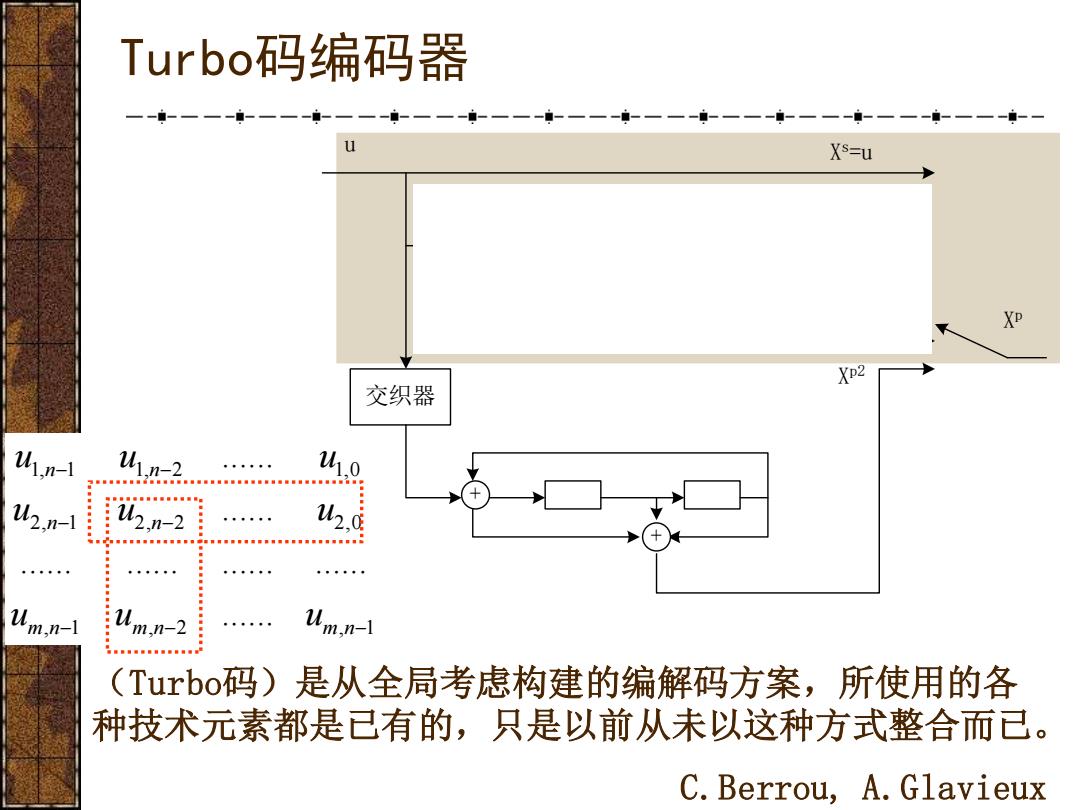
Turbo码编码器 Xs=u XP XP2 交织器 4,n- U 1,n-2 .外 男年0用年用用用是g用图里。 U2,n-1月 2,n-2 1110n1日 Um.n-1 :u. m,n-2 Um.n-1 EAMnEEMnnana (Turbo码)是从全局考虑构建的编解码方案,所使用的各 种技术元素都是已有的,只是以前从未以这种方式整合而已。 C.Berrou,A.Glavieux
Turbo码编码器 + + 交织器 + + Xs=u Xp1 Xp2 Xp u (Turbo码)是从全局考虑构建的编解码方案,所使用的各 种技术元素都是已有的,只是以前从未以这种方式整合而已。 C.Berrou, A.Glavieux , 1 , 2 , 1 2, 1 2, 2 2,0 1, 1 1, 2 1,0 ...... ...... ...... ...... ...... ...... ...... − − − − − − − m n m n m n n n n n u u u u u u u u u

设2LwP L(ug)= P(44=0,(y,2,,yw》/P(04,2,yw》 ∑P(e,04,h,yw》 P(44=1,(0y,y2,yv》 e,uk= P(uk=0,(0y1,2,,yN) ∑P(e,(y,2,yx》 e,k=0 根据BCR算法(课本参考文献[12]) P(e,(,》码块为(yy2,y)同时在k时刻分支为e的概率 =P(sg(e),(y,2,,yk-i》P(s(e),yg/s-(e》P(yk+1yk+2,yw)/s(e》 x(S)=P(s,(y,2,,y) Y(e)=P(s(e).v:Isj(e)) 注意:s(e)=s(e)s-(e) B()=P(yk+1,yk+2,,yN)/S) e P(e,(y,2,,yw))=&k-1(s(e)y(e)B(s(e) i-(e),ck-1(e) >a(s(e)r:(e)B(sj(e)) Sk-s(e)… L(ug)=In e,k=] ∑a4-(s-(e7(e)p,(s(e) k-1时刻 k时刻 e,ug =0
= = = = = = = = = = = = = − = − − + + − − − − − − + + = = , 0 1 1 , 1 1 1 1 2 1 1 1 2 1 1 1 1 2 1 1 2 1 1 1 2 1 2 , 0 1 2 , 1 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ( ( )) ( ) ( ( )) ( ( )) ( ) ( ( )) ( ) ln ( ,( , ,...,, )) ( ( )) ( ) ( ( )) ( ) (( , ,...,, )/ ) ( ) ( ( ), / ( )) ( ) ( ) ( ) ( ,( , ,...,, )) ( ( ),( , ,...,, )) ( ( ), / ( )) (( , ,...,, )/ ( )) ( ,( , ,..., )) BCJR [12]) ( ,( , ,...,, )) ( ,( , ,...,, )) ln ( 0,( , ,...,, )) ( 1,( , ,...,, )) ln ( 0,( , ,...,, ))/ (( , ,...,, )) ( 1,( , ,...,, ))/ (( , ,...,, )) ( ) ln k k k k e u S k k k S k k e u S k k k S k k k S k k k S N k k k k k N S k E k S k k E k k k k S k k N k S k k S k k S k N e u N e u N k N k N k N N k N N k s e e s e s e e s e L u P e y y y s e e s e s P y y y s e P s e y s e s e s e s P s y y y P s e y y y P s e y s e P y y y s e P e y y y P e y y y P e y y y P u y y y P u y y y P u y y y P y y y P u y y y P y y y L u - - = - 注意: = 根据 算法(课本参考文献 设yk=(y s k , y p k ) 码块为(y1,y2 ,…., yN)同时在k时刻分支为e的概率 Sk-1 S(e) SE k-1(e) k-1时刻 k时刻 e uk-1(e),ck-1(e)

ak(s)=P(s ,(yi,y22...,)) 前k个码字为y1,y2,,y)同时在k时刻到达状态为s的概率 体现了时刻k之前的码元对当前信息位,的影响 Y:(e)=P(sk(e),ygIs(e)) 注意:s(e)=s(e) 在k-1时刻到达状态为s,(e)的条件下,信息比特为y,同时时刻 转移到状态s1(e) rk(e)=P(s(e)/s(e))P(ygIs(e),s(e))=P(ug)P(yg/ux) B(s)=P((vk,yk+2....Yx)/s 接收码 y1 y2 Yk+2 时刻012 kk+1 N 在时刻到达状态为s的条件下 后N-k个码字为(yk+1,yk+2,,yN)的概率 S-(e) 体现了时刻k之后的码元对当前信息位,的影响 P(e,(Y1,Y2>....Yx))=ak-(s(e)r(e)B:(sj(e)) 由于充分考虑了前后的信息,因此误码率大大降低
由于充分考虑了前后的信息,因此误码率大大降低 = 体现了时刻 之后的码元对当前信息位 的影响 后 个码字为 的概率 在 时刻到达状态为 的条件下 转移到状态 在 时刻到达状态为 的条件下,信息比特为 ,同时 时刻 注意: = 体现了时刻 之前的码元对当前信息位 的影响 前 个码字为 同时在 时刻到达状态为 的概率 ( ,( , ,...,, )) - ( ( )) ( ) ( ( )) ( , ,...,, ) ( ) (( , ,...,, )/ ) ( ) ( ( )/ ( )) ( / ( ), ( )) ( ) ( / ) ( ) 1 ( ) ( ) ( ( ), / ( )) ( ) ( ) ( , ,...,, ) ( ) ( ,( , ,...,, )) 1 2 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 1 2 1 2 P e y y y s e e s e k u N k y y y k s s P y y y s e P s e s e P y s e s e P u P y u s e k s e y k e P s e y s e s e s e k u k y y y k s s P s y y y S k k k S N k k k k k N k k k N k k k S k E k k S k E k k E k k S k S k E k S k k E k k k k k k − + + + + − − − − − − − − − − = = = − = = 0 1 2 …… k-1 k k+1 …… N Sk-1 S(e) SE k-1(e) 时刻 接收码 y1 y2 …… yk-1 yk yk+1 yk+2 ……yN e uk-1(e)

e.04)4-@rea.e ax(S)=P(s,(yiy2>....)) SE(e) Y:(e)=P(s(e).yx/s(e)) 注意:s(e)=s(e) ⊙ f(S)=P(yk+1,yk+2,,yN)/s)) ux(e),Cx(e) 考虑到分量编码器相当于马尔可夫源 S.S(e) a4(s2(e》=P(s2(e),(y,2,y》 k时刻 k十1时刻 =∑P(s(ehsE(e),(yy2,,y)》 =∑P(s(eh0,y2,yk-P(s是(ey/s(e)》s.e =∑ak-(s(e)M(e) k-1e),Ck-(e) B-(s(e))=P((yxx)/(e)) S-s(e) =∑P(s(e)(0yk,yk+2,yw)/s-(e》 k-1时刻 k时刻 =∑P(yk+,k+2,yw)/s(e)P(si(e),y/sai(e》 =∑B.(s(e)m(e)
( ( )) ( ) (( , ,...,, )/ ( )) ( ( ), / ( )) ( ( ) ( , ,...,, )/ ( )) ( ( )) (( , ,...,, )/ ( )) ( ( )) ( ) ( ( ) ( , ,...,, )) ( ( ), / ( ))) ( ( ) ( ),( , ,...,, )) ( ( )) ( ( ),( , ,...,, )) ( ) (( , ,...,, )/ ) ( ) ( ( ), / ( )) ( ) ( ) ( ) ( ,( , ,...,, )) ( ,( , ,...,, )) ( ( )) ( ) ( ( )) 1 2 1 1 2 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 2 1 2 1 1 1 1 2 1 2 1 1 s e e P y y y s e P s e y s e P s e y y y s e s e P y y y s e s e e P s e y y y P s e y s e P s e s e y y y s e P s e y y y s P y y y s e P s e y s e s e s e s P s y y y P e y y y s e e s e k e S k k S k k E k e S k k N k e S k k N k S k S k k N k S k k k e S k k S k k E k e k S k e k E k S k k E k S k k k k k N S k E k S k k E k k k k S k k k S N k k = = = = = = = = = + + − − + − − − + − − − − − − − − − − + + − − − − = , , = , 考虑到分量编码器相当于马尔可夫源 注意: = = - Sk S(e) Sk E(e) k时刻 k+1时刻 e uk (e),ck (e) Sk-1 S(e) SE k-1(e) k-1时刻 k时刻 e uk-1(e),ck-1(e)
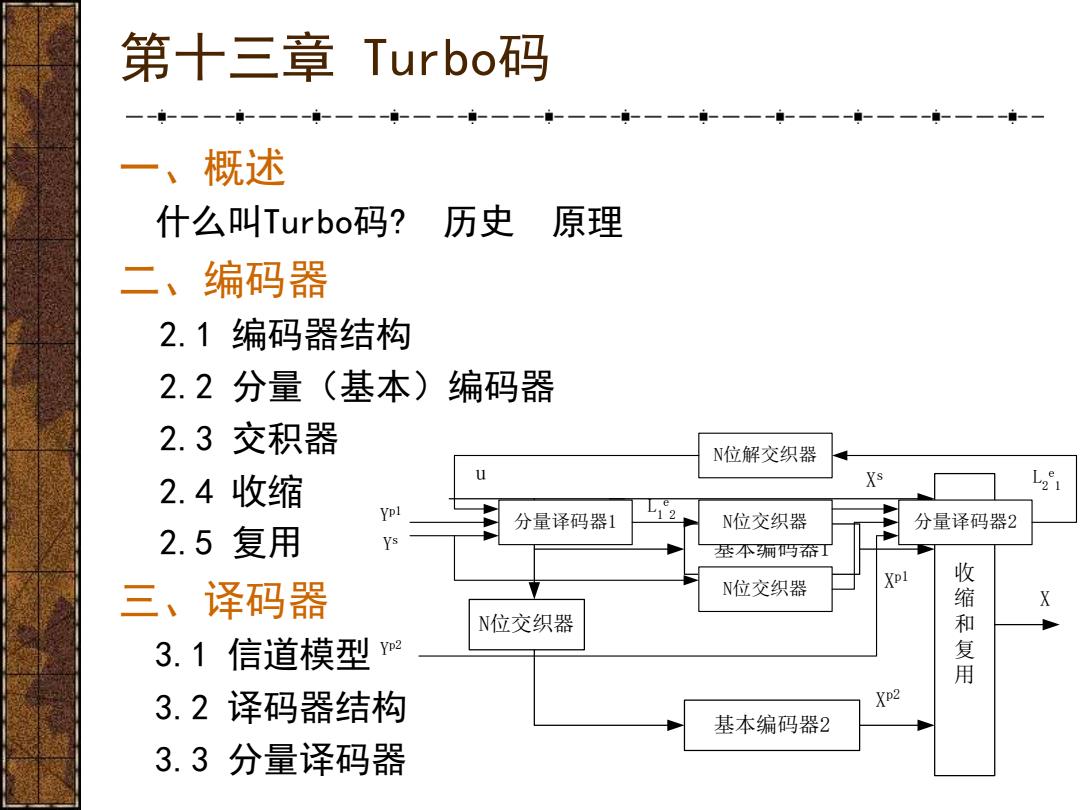
第十三章Turboi码 一、 概述 什么叫Turbo?码? 历史 原理 二、编码器 2.1编码器结构 2.2分量(基本)编码器 2.3交积器 N位解交织器 2.4收缩 Xs 分量译码器1 N位交织器 分量译码器2 2.5复用 Ys 基本厢吗爷丁 三、译码器 N位交织器 收缩和复用 X N位交织器 3.1信道模型 3.2译码器结构 XD2 基本编码器2 3.3分量译码器
第十三章 Turbo码 一、概述 什么叫Turbo码? 历史 原理 二、编码器 2.1 编码器结构 2.2 分量(基本)编码器 2.3 交积器 2.4 收缩 2.5 复用 三、译码器 3.1 信道模型 3.2 译码器结构 3.3 分量译码器 基本编码器1 基本编码器2 N位交织器 收 缩 和 复 用 u X Xs Xp1 Xp2 N位解交织器 N位交织器 N位交织器 分量译码器1 分量译码器2 Ys Yp1 Yp2 L1 e 2 L2 e 1

一、Trubo码概述 米Turbo--涡轮发动机 PASSAT T:Turbo 涡轮增压装置 8下
一、Trubo码概述 Turbo --- 涡轮发动机 T: Turbo 涡轮增压装置
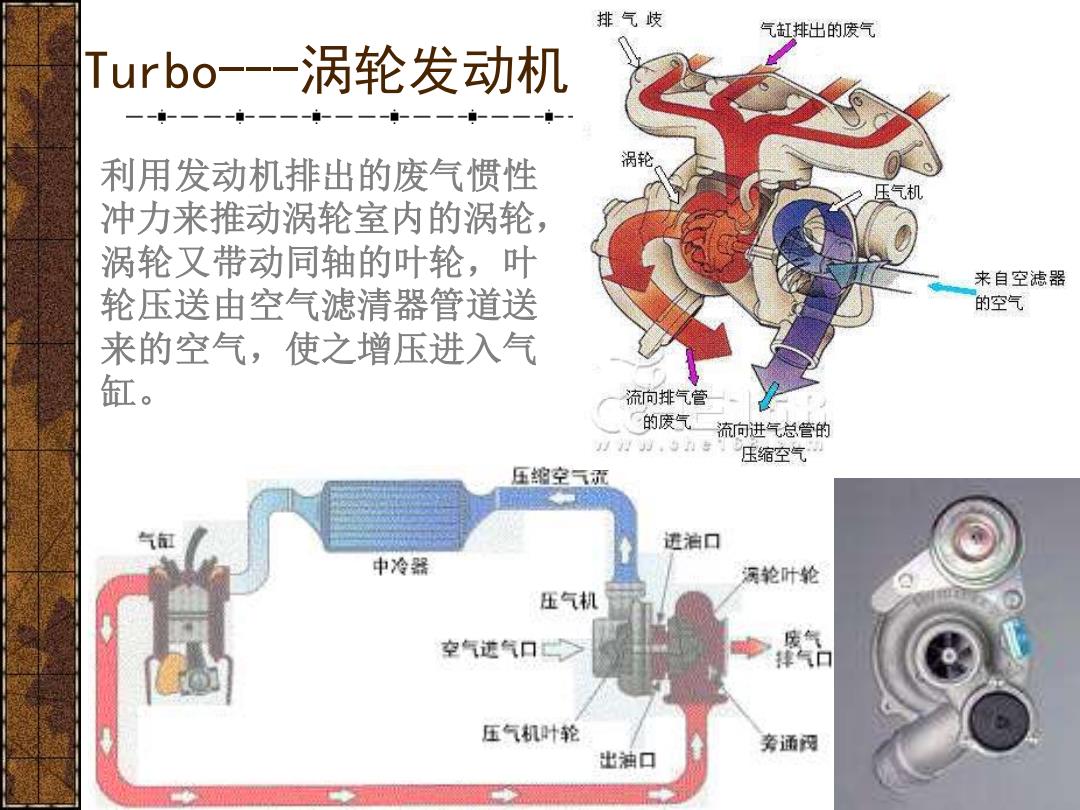
排气歧 气缸排出的废气 Turbo--涡轮发动机 利用发动机排出的废气惯性 涡轮 冲力来推动涡轮室内的涡轮, 涡轮又带动同轴的叶轮,叶 来自空滤器 轮压送由空气滤清器管道送 的空气 来的空气,使之增压进入气 缸。 流向排气管一、 的废气 流向进气总管的 力,专压缩空气 压控空气流 进泊口 中冷器 润轮叶轮 压气机 空气送气口 气口 压气机叶轮 旁通网 出油口
Turbo---涡轮发动机 利用发动机排出的废气惯性 冲力来推动涡轮室内的涡轮, 涡轮又带动同轴的叶轮,叶 轮压送由空气滤清器管道送 来的空气,使之增压进入气 缸
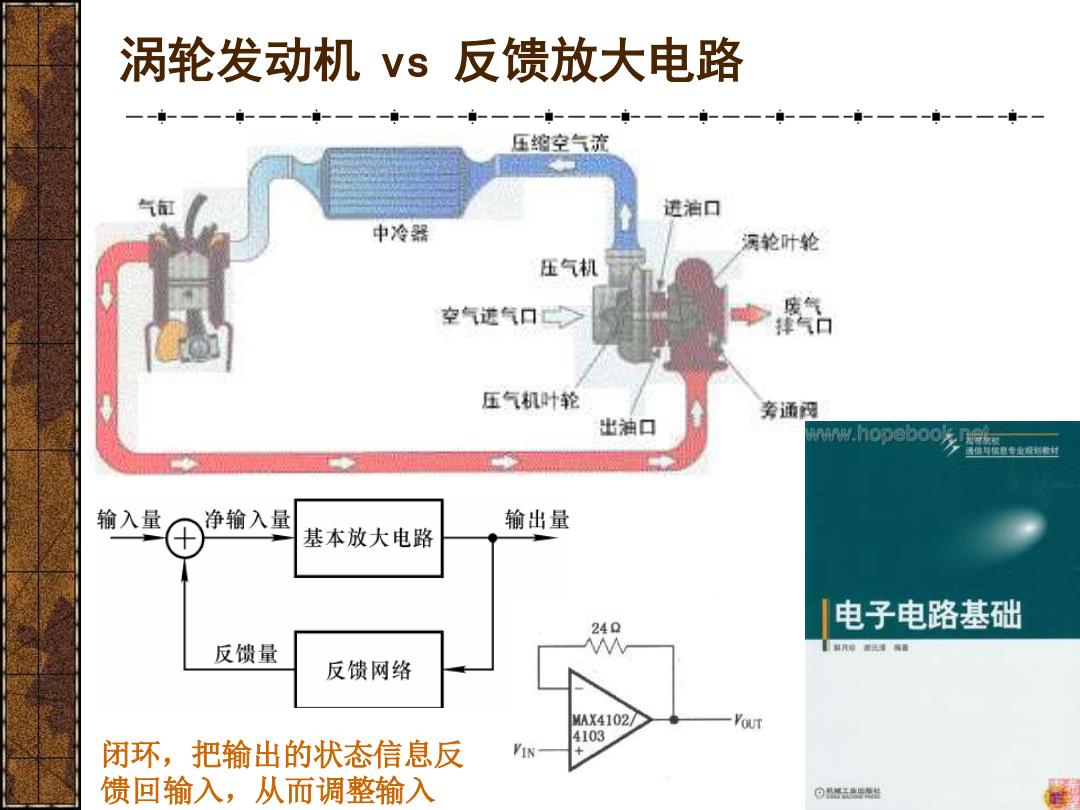
涡轮发动机Vs反馈放大电路 压控空气流 气缸 进泊口 中冷器 深轮叶轮 压气机 空气送气口◆ 废 气口 压气机叶轮 奢通阀 出油口 房优e电e过 输入量 净输入量 输出量 基本放大电路 24Q 电子电路基础 反馈量 月峰语 反馈网络 MAX4102/ VouT 4103 闭环,把输出的状态信息反 馈回输入,从而调整输入 ⊙出
涡轮发动机 vs 反馈放大电路 闭环,把输出的状态信息反 馈回输入,从而调整输入

香农第二定理(有噪信道编码定理) 1948年 如一个离散无记忆信道,信道容量为C。当信息传输率 R≤C时,只要码长足够长,总可以在输入符号集中X"找到 M(=2)个码字组成的一组码(2R,n)和相应的译码准则,使 信道输出端的平均错误译码概率达到任意小。 可能性, 如何找? Claude 1938年在MIT获得电气工程硕士学位,硕 Elwood 士论文题目是《A Symbolic Analysis of 没有给出答案 Shannon Relay and Switching Circuits》(继电器与 1916-2001 开关电路的符号分析)。用布尔代数分析并优 化开关电路,奠定了数字电路的理论基础。 “这可能是本世纪最重要、最著名的一篇硕 士论文。”(Howard Gardner,哈佛大学 教授) 1940年在MIT获得数学博士学位,博士论 文是关于人类遗传学的,题目是《An Algebra for Theoretical Genetics) (理论 遗传学的代数学)
香农第二定理(有噪信道编码定理) 1948年 如一个离散无记忆信道,信道容量为C。当信息传输率 R≤C时,只要码长足够长,总可以在输入符号集中 找到 M 个码字组成的一组码 和相应的译码准则,使 信道输出端的平均错误译码概率达到任意小。 n X ( 2 ) nR = (2 , ) nR n 可能性, 如何找? 没有给出答案 Claude Elwood Shannon 1916-2001 1938年在MIT获得电气工程硕士学位,硕 士论文题目是《A Symbolic Analysis of Relay and Switching Circuits》(继电器与 开关电路的符号分析)。用布尔代数分析并优 化开关电路,奠定了数字电路的理论基础。 “这可能是本世纪最重要、最著名的一篇硕 士论文。”(Howard Gardner,哈佛大学 教授) 1940年在MIT获得数学博士学位,博士论 文是关于人类遗传学的,题目是《An Algebra for Theoretical Genetics》(理论 遗传学的代数学)