
第四章多项式与有限域 陆以勤 -一一--一一--一一--一一-
第四章 多项式与有限域 陆以勤

米学习本章目的:对Xn-1进行因式分解(n=gm-1,q为素数) X15-1=(x+1)(x4+x3+1)(x4+x3+x2+x+1)(x2+x+1)(x4+x+1) 米Xn-1? 循环:只有最高位和最低位
学习本章目的:对X n-1进行因式分解(n=qm-1,q为素数) X 15-1=(x+1)(x 4 + x 3+1)(x 4+x3+x2 +x +1)(x 2 +x +1)(x 4+x +1) X n-1? 循环:只有最高位和最低位

一、剩余类环 1. 环,子环、扩环 回顾环(R,+,*)的定义 米定义了两种运算+和* 米 R对+构成阿贝尔群 米 *满足封闭性、结合律 米 *对+满足分配律 米 *不一定有恒等元1,R的元素不一定有逆元 2. 非空子集S是环(R,+,*)的子环的充要条件: 1)Va,beS:a-b∈S;S是群(R,+)的子群 2)Va,beS:ab∈SS对*满足封闭性
一、剩余类环 1. 环,子环、扩环 回顾环(R,+, *)的定义 定义了两种运算+和* R对+构成阿贝尔群 *满足封闭性、结合律 *对+满足分配律 *不一定有恒等元1,R的元素不一定有逆元 2. 非空子集S是环(R,+, *)的子环的充要条件: 1) a,b S:a-b S ; S是群(R,+)的子群 2) a,b S:ab S S对*满足封闭性

一、剩余类环 3。 理想 定义:交换环冲的非空子集/称为冲的理想,若: l)Ha,b∈I:a-b∈I; 2)Ha∈/,r∈R.ar=ra∈I, )+2)三理想是个子环, 2)三/中任一元素a的倍数在/中,即/由的一些元素 (可以是多个)的倍数组成。 米 主理想:由一个元素的的所有倍数组成的理想.这 个元素叫生成元. 米 主理想环:每一个理想都是主理想
一、剩余类环 3. 理想 定义: 交换环R中的非空子集I称为R中的理想,若: 1) a, b I: a-b I; 2) a I, r R: ar =ra I; 1)+2) 理想是个子环, 2) I 中任一元素a的倍数在I中,即I由R的一些元素 (可以是多个)的倍数组成。 主理想:由一个元素的的所有倍数组成的理想.这 个元素叫生成元. 主理想环:每一个理想都是主理想
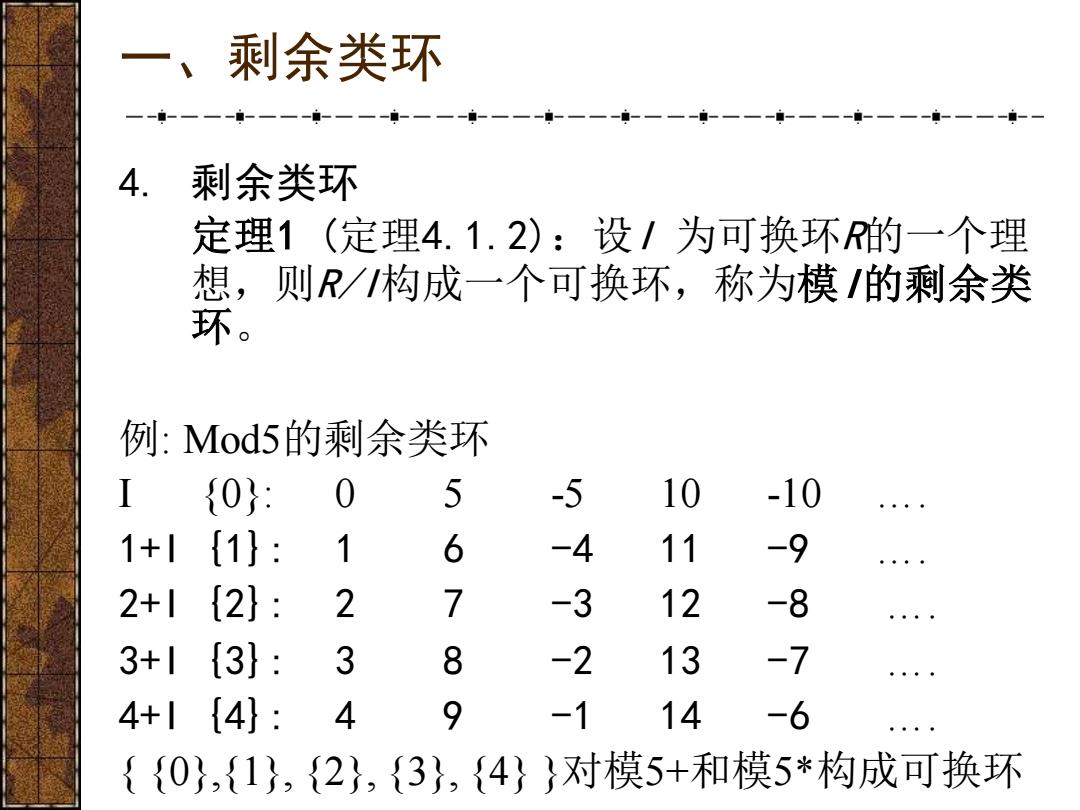
一、剩余类环 4. 剩余类环 定理1(定理4.1.2):设/为可换环R的一个理 ,则R/1构成一个可换环,称为模/的剩余类 环 例:Mod5的剩余类环 {0}: 0 5 -5 10 -10 1+1 {1}: 1 6 -4 11 -9 2+1{2}: 2 7 -3 12 -8 3+1{3}: 3 8 -2 13 -7 4+1{4}: 4 9 一1 14 -6 {{0},{1},{2},{3},{4}}对模5+和模5*构成可换环
一、剩余类环 4. 剩余类环 定理1 (定理4.1.2):设I 为可换环R的一个理 想,则R/I构成一个可换环,称为模I的剩余类 环。 例: Mod5的剩余类环 I {0}: 0 5 -5 10 -10 …. 1+I {1}: 1 6 -4 11 -9 …. 2+I {2}: 2 7 -3 12 -8 …. 3+I {3}: 3 8 -2 13 -7 …. 4+I {4}: 4 9 -1 14 -6 …. { {0},{1}, {2}, {3}, {4} }对模5+和模5*构成可换环

二、多项式剩余类环 1. 多项式 Fq上的多项式: f(x)=fnxn +fn-1x"-1+...+f2x2+f1x +fo f;∈Fqi=0,1,2,,n 次数n记为:of(x),o°f,degf(x),degf 米 Why多项式? 矢量 a=(1,0,1,1,0,1) (位置) 多项式f(x)=x5+x3+x2+1 (次数) 为了借用多项式的运算来定义矢量的运算 多项式的除法例:(x+x8+x7+x2+x+1)/(x4+x3+×+1) 米 n次多项式域(群、环)与n维矢量域(群、环)在 下列映射下同构: f(x)=fnxn +fn-1x-1+...+f2x2+f1x +fo>(fnfn-1...f2fifo)
二、多项式剩余类环 1. 多项式 Fq上的多项式: f(x)= fnx n +fn-1x n-1+…+f2x 2 +f1x +f0 fi Fq i=0,1,2,…,n 次数n记为:f(x), f, degf(x), degf Why多项式? 矢量 a = (1,0,1,1,0,1) (位置) 多项式f(x)= x5 +x3+x2 +1 (次数) 为了借用多项式的运算来定义矢量的运算 多项式的除法 例:(x 9+x8 +x7 +x2+x +1)/(x 4+ x3 + x +1) n次多项式域(群、环)与n维矢量域(群、环)在 下列映射下同构: f(x)= fnx n +fn-1x n-1+…+f2x 2 +f1x +f0 → ( fnfn-1…f2f1f0)

二、多项式剩余类环 米 定理2:集合G与G同构→(G为群(环、 域)一G为群(环、域)) 米 首一多项式:f。=1,最高次数为1, a°f(x)≥1。 米 Fq[x]:表示系数属于Fq的所有多项式的集 合 2. 多项式环 整数是一个环,多项式与整数类似。 定理3:F。[x]构成一个环 零元:f(x)=0
二、多项式剩余类环 定理2:集合G与G 同构 (G为群(环、 域) G为群(环、域) ) 首一多项式: fn =1,最高次数为1, f(x)1。 Fq[x]: 表示系数属于Fq的所有多项式的集 合 2. 多项式环 整数是一个环,多项式与整数类似。 定理3:Fq [x]构成一个环 零元:f(x)=0

二、多项式剩余类环 性质 整数环 多项式环 零元素 0 f(x)=0 恒等元 1 f(x)=1 不可分 素数 米既约多项式(除提取常数,不能 解的元 进行因式分解,定义4.4.2) 素多项式=首一+既约多项式 分解的 a=pp22 f(x)=p1(x)r1p2(x)r2. 唯一性 (素数幂的积) 每一个首一多项式可唯一分解为 素多项式的幂的积(定理4.2.3) 欧几里 若a>b,则a可唯 若a°f(x)>O°g(x),则: 德除法 一表示为: f (x)=q(x)g(x)+r(x) a=qb+r,0≤r≤b 0≤a°r(x)≤a°g(x)(定理4.2.2)
二、多项式剩余类环 性质 整数环 多项式环 零元素 0 f(x)=0 恒等元 1 f(x)=1 不可分 解的元 素数 既约多项式(除提取常数,不能 进行因式分解,定义4.4.2) 素多项式=首一 + 既约多项式 分解的 唯一性 a=p1 r1p2 r2… (素数幂的积) f(x)=p1(x)r1p2 (x) r2… 每一个首一多项式可唯一分解为 素多项式的幂的积(定理4.2.3) 欧几里 德除法 若a>b,则a可唯 一表示为: a=qb+r,0 r b 若f(x) > g(x),则: f(x) =q(x)g(x)+r(x) 0 r(x) g(x) (定理4.2.2)

二、多项式剩余类环 性质 整数环 多项式环 约数 最大公约数 最高公因式(定义4.2.3)(是首一多项式) (a,b),GCD(a,b) (f (x),g(x)),GCD(f (x),g(x)) 倍数 最小公倍数 最低公倍式(定义4.2.4)(是首一多项式) [a,b],LCM(a,b) [f (x),g(x)],LCM(f (x),g(x)) 欧几 a=qb+r→ f(x)=q(x)g(x)+r(x)→ 里德 (a,b)=(b,r) (f(x),g(x))=(g(x),r(x) 算法 (a,b)=Aa+Bb (例f(x)=x+x8+x7+x2+x+1,g(x)=x4+x3+x+1) A,B为正整数 (f(x),g(x))=A(x)f(x)+B(x)g(x) 0≤OA(x)<o°g(x)-a°(f(x),g(x) 0≤aB(x)<a°f(x)-a°(f(x),g(x)) [a,b]=ab/(a,b) [f(x),g(x)]=f(x)g(x)/(f(x),g(x))
二、多项式剩余类环 性质 整数环 多项式环 约数 最大公约数 (a,b),GCD(a,b) 最高公因式(定义4.2.3)(是首一多项式) (f(x),g(x)), GCD(f(x),g(x)) 倍数 最小公倍数 [a,b],LCM(a,b) 最低公倍式(定义4.2.4)(是首一多项式) [f(x),g(x)], LCM(f(x),g(x)) 欧几 里德 算法 a=qb+r (a,b)=(b,r) (a,b)=Aa+Bb A,B为正整数 f(x) =q(x)g(x)+r(x) (f(x),g(x))=(g(x),r(x)) (例f(x)= x 9+x8+x7+x2+x+1,g(x)=x4+x3+x+1) (f(x),g(x))=A(x)f(x)+B(x)g(x) 0 A(x)< g(x)- (f(x),g(x)) 0 B(x)< f(x)- (f(x),g(x)) [a,b]=ab/(a,b) [f(x),g(x)]=f(x)g(x)/(f(x),g(x))

二、多项式剩余类环 性质 整数环 多项式环 主理 m为生成元(m的一 以f(x)为生成元:f(x)的一切倍式 想1 切倍数的集合) 组成的集合!)组成一个理想 (引理4.2.1)例1x+1) 剩余 以模m的剩余类为 以f(x)对1fx)的陪集为元素,记为 类环 元素,记为Zn或 Fq[x]/f(x) (定理4.2.8) Z/(m) 主理 是主理想环 是主理想环 (定理4.2.10) 想环 有限 m为素数台Z.是一 f(x)为既约多项式台Fq[x]/f(x) 域 个域 是一个域 (定理4.2.9)
二、多项式剩余类环 性质 整数环 多项式环 主理 想I m为生成元(m的一 切倍数的集合) 以f(x)为生成元:f(x)的一切倍式 组成的集合If(x)组成一个理想 (引理4.2.1) 例 I(x2+1) 剩余 类环 以模m的剩余类为 元素,记为Zm或 Z/(m) 以f(x)对If(x) 的陪集为元素,记为 Fq[x]/f(x) (定理4.2.8) 主理 想环 是主理想环 是主理想环 (定理4.2.10) 有限 域 m为素数 Zm是一 个域 f(x)为既约多项式 Fq[x]/f(x) 是一个域 (定理4.2.9)