
数学(一) 第四章:反三角函数
反三角函数 数学(一) 第四章:反三角函数

第二部分第一讲: 反正弦函数的图像 主讲人:卢自娟
反三角函数 第二部分第一讲: 反正弦函数的图像 主讲人:卢自娟

反三角函数 引例 当sinc=时,你能求出满足等式的角α吗? 2 显然,sing= 除了a=时,你还能找出满足等式的其它角α吗? sin(2kr+F=2,(k∈Z), 如果限定在一个周期[0,2π]上,此时只有一个角 满足条件吗? 5m1 sin 6=
反三角函数 引例

反三角函数 引例 如何限定角的范围,才能达到只有一个角 满足方程? sina 2 [- 器 f(x)=sin(x) π3π 【22 C 3π 2
反三角函数 引例 [ − ᵰ 2 , ᵰ 2 ]

反三角函数 引例 正弦函数y=sinx,在(-oo,+o)上有没有反函数? y =sind 19 0 0 2n 3元 4n x 2
反三角函数 引例

反三角函数 1.反正弦函数 定义1把正弦函数y=simx,xE[-,引的反函数 叫做反正弦函数,记作y=arcsinx或y=sin-1x. (1)定义域D=[-1,1] (2)值域M=-2] (3)公式sin(arcsin x)=x,x∈[-1,1] arcsin(-x)=-arcsinx ,x E [-1,1]
反三角函数 1.反正弦函数
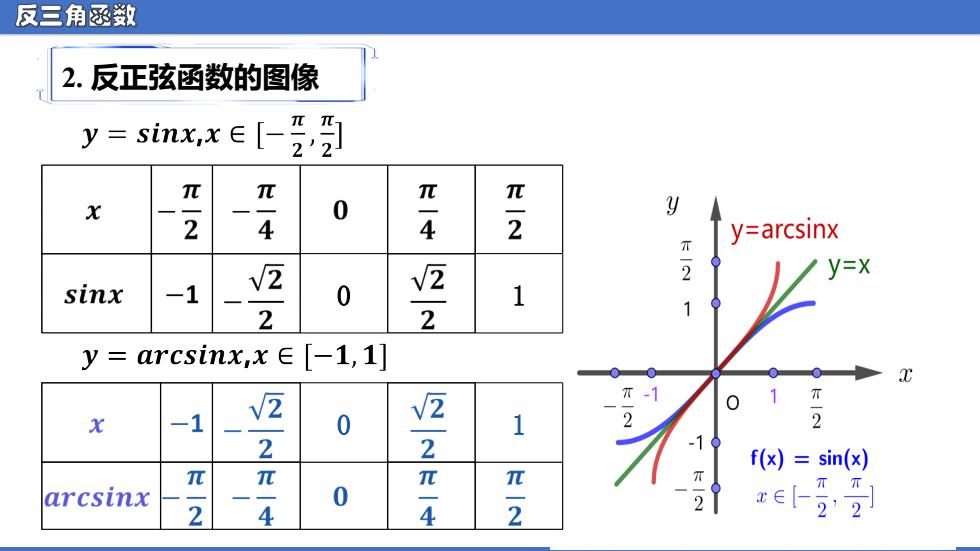
反三角函教 2.反正弦函数的图像 y=sinx,xe[ π π X 0 4 元2 y 4 y=arcsinx sinx -1 V2 V2 2 /y=x 0 1 2 y=arcsinx,x[-1,1] -1 V2 T-1 0 V2 1 2 2 2 2 -10 f(x)=sin(x) 元 元 π arcsinx 0 TT 2 4 4 2 2 xe-2'2
反三角函数 2. 反正弦函数的图像 0 1 0 1

反三角函数 3.反正弦函数的性质 y=arcsinx,x∈[-1,1] y (4)单调性 单调递增 y=arcsinx 2 (5)有界性 有界 (6)奇偶性 奇函数 (7)周期性 没有周期性
反三角函数 3. 反正弦函数的性质 (4) 单调性 (5) 有界性 (6) 奇偶性 (7) 周期性 单调递增 有界 奇函数 没有周期性

反三角函教 4.反正弦函数值 acsin 0=0 arcsin arin 1=z 26 aresin( 3 元 0= 3 3 元 arcsin 2 3 元 4 arcsin 2 4 n?=1 1=匹 ain(-1)=-匹 acin 2 2 2
反三角函数 4. 反正弦函数值 ᵈᵉᵈᵉᵈᵈ ᵼ = ᵼ ᵈᵉᵈᵉᵈᵈ ᵼ ᵽ = ᵴ ᵽ ᵈᵉᵈᵉᵈᵈ ᵼ = ᵴ ᵽ ᵈᵉᵈᵉᵈᵈ ( − ᵼ ) = − ᵴ ᵽ ᵉᵈᵈ ? = ᵼ ᵽ

反三角函数 思考 1.y=sinx,x∈[-]与y=sin-样吗? 2.y=sinx,x∈[受,]有反函数吗?
反三角函数 思考