
薇率论与数理统计课程教案 1 《概率论与数理统计》课程教案 主讲教师 所在单位 授课班级 专业 撰写时间 教案编号18-0702 教案内容7.3估计量的评选标准: 学时1 基本要求(①)会判断估计量的无偏性、有效性的概念,理解一致性的概念 1.培养能力要求: a)掌握概率论和数理统计中的基本概念和性质并能够运用到复杂工程 教学目标 能力要求 问题的适当表述之中: b)能够根据试验或观察得到的数据来研究随机现象,运用参数估计和 假设检验等基本的统计方法,对客观规律性做出合理的估计和判断 以解决实际问题。 教学重点分布参数估计量的评价准则 教学难点 教学方法提问、讨论、讲授、启发、示例、板书、PPT 工具仪器多媒体教具、教材、教案、教学课件、考勒表、平时成绩登记表 教学安排考勤、复习相关知识点、新课内容概述、组织教学、布置作业、课后小结 教学过程教学组织、具体教学内容及教学方法、手段、时间分配及其它说明 备注 第一部分:旧知识点复习和新课内容概述们分钟) 板书, 在上一节中,我们学习了分布参数的点估计。根据估计量的选取方法不同,我回顾 们重点学习了矩估计和最大似然估计。 由点估计的两种典型求估计量的方法可知,同一参数用不同的估计方法,求出 的估计量可能不同。 比如&可以是前k阶样本矩的函数(假设有k个待估参数),也可以是样本似PT 然函数的极点或在取值范围内的最值点 如均匀分布中关于区间两个端点的矩估计量和最大似然估计量就不同。 尽管原则上,任何统计量都可以作估计量,但总有好坏之分,希望在合理的标准了 选择最理想的估计量: 本节学习三个常用的评选标准:无偏性,有效性,相合性(一致性) 第二部分:无偏性(18分钟) 1°无偏性一一数学期望评选标准 意义:估计量是随机变量,其所取估计值应以待估参数真值为中心摆动,并且大量
概率论与数理统计课程教案 1 《概率论与数理统计》课程教案 主讲教师_ 所在单位_ 授课班级_ 专业_ 撰写时间_ 教案编号 18-0702 教案内容 7.3 估计量的评选标准; 学时 1 教学目标 基本要求 (1)会判断估计量的无偏性、有效性的概念,理解一致性的概念; 能力要求 1. 培养能力要求: a) 掌握概率论和数理统计中的基本概念和性质并能够运用到复杂工程 问题的适当表述之中; b) 能够根据试验或观察得到的数据来研究随机现象,运用参数估计和 假设检验等基本的统计方法,对客观规律性做出合理的估计和判断, 以解决实际问题。 教学重点 分布参数估计量的评价准则 教学难点 教学方法 提问、讨论、讲授、启发、示例、板书、PPT 工具仪器 多媒体教具、教材、教案、教学课件、考勤表、平时成绩登记表 教学安排 考勤、复习相关知识点、新课内容概述、组织教学、布置作业、课后小结 教学过程 教学组织、具体教学内容及教学方法、手段、时间分配及其它说明 备 注 第一部分:旧知识点复习和新课内容概述(7 分钟) 在上一节中,我们学习了分布参数的点估计。根据估计量的选取方法不同,我 们重点学习了矩估计和最大似然估计。 由点估计的两种典型求估计量的方法可知,同一参数用不同的估计方法,求出 的估计量可能不同。 比如 θ 可以是前 k 阶样本矩的函数(假设有 k 个待估参数),也可以是样本似 然函数的极点或在取值范围内的最值点 如均匀分布中关于区间两个端点的矩估计量和最大似然估计量就不同。 尽管原则上,任何统计量都可以作估计量,但总有好坏之分,希望在合理的标准下 选择最理想的估计量: 本节学习三个常用的评选标准:无偏性,有效性,相合性(一致性) 第二部分:无偏性(18 分钟) 1°无偏性――数学期望评选标准 意义:估计量是随机变量,其所取估计值应以待估参数真值为中心摆动,并且大量 板书, 回顾 PPT

估计值的统计平均值应该稳定于参数真值,也就是估计量的数学期望应该等于参 数真值 设X,X2,.,X是总体X的一个样本,0∈日是包含在总体X的分布中的待估参 数这里日是)的取值范围。 无偏性若估计量0=(X1,X2,.,X)的数学期望E)存在,且对于任意的8日有 ()=8,则称是8的无偏估计量 即E0)-0=0, 称E(©)一&为以作为0的估计的系统误差,那么无偏估计的实际意义就是无 系统误差。(人为的或系统本身原因导致的误差,而不是测量误差) 例如:设总体X的k阶矩,期望和方差分别为k,4,2 由于2x上2-24 2x-o2 x=E明之x)=u 所以k阶样本矩,样本方差和样本均值分别为k阶总体矩,方差σ和期望 μ的无偏估计量 而0的一个告计量。=6=之X-y由于 (B之cx,-上"。≠0,因而是有偏的 n 其中,由方差恒等式EX2)=DX)+EX)2 B=空x-=280X)-H22+)-o2m+r 因此,一般取S2作为总体方差的无偏估计量 例2:设总体X服从参数为9的指数分布,X,X2,X是总体X的一个样本,试证: x和nZ=nmin(X,X2,Xa】都是0的无偏估计量 证:1°显然有(x)=EX=0,成立 2°Z=min(X,X2.,X)具有概率密度1-1-fxm=1-1-(1-eoP 侵”做新国=n 所以Enz)=,也成立 一个参数可以有不同的无偏估计量。那么进一步的这两个无偏估计量哪一个
2 估计值的统计平均值应该稳定于参数真值,也就是估计量的数学期望应该等于参 数真值 设 X1,X2,.,Xn 是总体 X 的一个样本,θ Θ 是包含在总体 X 的分布中的待估参 数这里Θ是 θ 的取值范围。 无偏性 若估计量 = (X1,X2,.,Xn)的数学期望 E( )存在,且对于任意的 θ Θ 有 E( )=θ,则称 是 θ 的无偏估计量。 即 E( )-θ=0, 称 E( )-θ 为以 作为 θ 的估计的系统误差,那么无偏估计的实际意义就是无 系统误差。(人为的或系统本身原因导致的误差,而不是测量误差) 例如:设总体 X 的 k 阶矩,期望和方差分别为 μk,μ,σ 2 由于 E(Ak)=E( )= = =μk E(S 2 )=E( )=σ 2, E( )=E( )=μ 所以 k 阶样本矩,样本方差和样本均值分别为 k 阶总体矩 μk,方差 σ 2 和期望 μ 的无偏估计量 而 σ 2的一个估计量 =B2= 由于 E(B2)= E( )= ≠σ 2,因而是有偏的 其中,由方差恒等式 E(X2 )=D(X)+E(X)2 E(B2)=E( )= = 因此,一般取 S 2作为总体方差的无偏估计量 例 2:设总体 X 服从参数为 θ 的指数分布,X1,X2,.,Xn是总体 X 的一个样本,试证: 和 nZ=n[min(X1,X2,.,Xn)]都是 θ 的无偏估计量 证:1°显然有 E( )=E(X)=θ,成立 2°Z=min(X1,X2,.,Xn)具有概率密度 1-[1-F(x)]n=1-[1-(1- )] n ,故有 E(Z)=θ/n, 所以 E(nZ)=θ,也成立 一个参数可以有不同的无偏估计量。那么进一步的这两个无偏估计量哪一个 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ = n i k Xi n 1 1 = n i k E Xi n 1 ( ) 1 = n i k n 1 1 = − − n i Xi X n 1 2 ( ) 1 1 X = n i Xi n 1 1 2 2 1 ( ) 1 X X n n i i − = = − n i Xi X n 1 2 ( ) 1 1 2 n n − = − n i Xi X n 1 1 2 2 = − n i E Xi E X n 1 2 2 ( ) ( ) 1 = + − + n i n n 1 2 2 2 2 ( ) ( / ) 1 X X x / e − = − 0, 其它 , 0 ( ; ) / min e x n f x nx

概率论与数理统计课程教案 更好些呢,这引出了以下标准 第三部分:有效性(10分钟) 2”有效性一 一方差评选标准(分散度)(评选的前提是二者首先是无偏的, 意义:待估参数可能有多个无偏估计量,但也有优劣之分 对于两个无偏估计量日和A,在样本容量n相同的条件下,哪一个估计量的 观察值更密集在真值日附近,认为哪一个更为理想。估计值与真值具有较大偏差 的概率就更小些。 由于方差是随机变量取值与其数学期望的偏离程度的度量,这样在无偏的情 况下E()=E(A)=0,以方差小者为好,即估计量的有效性 有效性设A=(仪1,X2,X)与A,=A,(X1,X2,X)都是9的无偏估计量,若对于任 意e⊙,有D(8sD(,)且至少对于某一个⊙,上式中的不等号成立,则称A较 A有效。 例2中的两个估计量的有效性 由于总体X的方差D(X)=2,因而有D()=DX)/n=0n 而由D(nZ)=n2D(2=n20/n2=02,所以D(n2>D(x),所以x较n2有效 第四部分相合性(10分钟) 3°相合性一一一样本容量极限评选标准 在样本固定情况下,无偏性和有效性都满足的估计量,其取值仍然是在真 值附近摆动,我们希望随着样本容量的增大,一个估计量的值稳定于待估参数 的真值。 相合性设日=(X1,X2,.,X)为参数0的估计量,若对于任意0e0,当n→∞时日 =X,X2,.,X)依概率收敛于9,则称为0的相合估计量 即,若对于任意的9eO都满足:对于任意的E>0,有 limP(10-0ks)=1 则称为0的相合估计量。 例如:样本k阶矩依概率收敛于总体k阶矩,样本k阶矩是总体k阶矩的相合估计 量,进一步的若待估参数0=g,2,.,则0矩估计量0=g(4,西,.,)=
概率论与数理统计课程教案 3 更好些呢,这引出了以下标准 第三部分:有效性(10 分钟) 2°有效性―――方差评选标准(分散度)(评选的前提是二者首先是无偏的) 意义:待估参数可能有多个无偏估计量,但也有优劣之分 对于两个无偏估计量 和 ,在样本容量 n 相同的条件下,哪一个估计量的 观察值更密集在真值 θ 附近,认为哪一个更为理想。估计值与真值具有较大偏差 的概率就更小些。 由于方差是随机变量取值与其数学期望的偏离程度的度量,这样在无偏的情 况下 E( )=E( )=θ,以方差小者为好,即估计量的有效性 有效性 设 = (X1,X2,.,Xn)与 = (X1,X2,.,Xn)都是 θ 的无偏估计量,若对于任 意 θ Θ,有 D( )D( )且至少对于某一个 θ Θ,上式中的不等号成立,则称 较 有效。 例 2 中的两个估计量的有效性 由于总体 X 的方差 D(X)=θ 2,因而有 D( )=D(X)/n=θ 2 /n 而由 D(nZ)=n 2D(Z)=n 2 (θ 2 /n 2 )=θ 2,所以 D(nZ)> D( ),所以 较 nZ 有效 第四部分 相合性(10 分钟) 3°相合性―――样本容量极限评选标准 在样本 n 固定情况下,无偏性和有效性都满足的估计量,其取值仍然是在真 值附近摆动,我们希望随着样本容量 n 的增大,一个估计量的值稳定于待估参数 的真值。 相合性 设 = (X1,X2,.,Xn)为参数 θ 的估计量,若对于任意 θ Θ,当 n→∞时 = (X1,X2,.,Xn)依概率收敛于 θ,则称 为 θ 的相合估计量 即,若对于任意的 θ Θ 都满足:对于任意的 ε>0,有 则称 为 θ 的相合估计量。 例如:样本 k 阶矩依概率收敛于总体 k 阶矩,样本 k 阶矩是总体 k 阶矩的相合估计 量,进一步的若待估参数 θ=g(μ1,μ2,.,μk),则 θ 矩估计量 =g( , ,., )= 1 ˆ 2 ˆ 1 ˆ 2 ˆ 1 ˆ 1 ˆ 2 ˆ 2 ˆ 1 ˆ 2 ˆ 1 ˆ 2 ˆ X X X ˆ ˆ ˆ ˆ ˆ | } 1 ˆ lim {| − = → P n ˆ ˆ 1 ˆ 2 ˆ k ˆ

g(A1,A2,·,A)是9的相合估计量。 ※由最大似然估计法得到的估计量,在一定条件下也具有相合性 ※相合性是对一个估计量的基本要求,若估计量不具有相合性,那么不论将样本 容量取得多么大,都不能将9估计得足够准确,因而不可取 可以用大数定律的思想处理。 课后作业 包括课后作业、数值实验作业、其它要求 课后小结是教案执行情况的经验总结,目的在于改进和调整教案,为下 课后小结 轮课讲授设计更加良好的教学方案。应全面审视教学过程,特别注意对意外发 现、点滴收获、以及因个别疏漏而及时补充的方法等方面的内容进行撰写
4 g(A1,A2,.,Ak)是 θ 的相合估计量。 ※ 由最大似然估计法得到的估计量,在一定条件下也具有相合性 ※ 相合性是对一个估计量的基本要求,若估计量不具有相合性,那么不论将样本 容量 n 取得多么大,都不能将 θ 估计得足够准确,因而不可取 可以用大数定律的思想处理。 课后作业 包括课后作业、数值实验作业、其它要求 课后小结 课后小结是教案执行情况的经验总结,目的在于改进和调整教案,为下一 轮课讲授设计更加良好的教学方案。应全面审视教学过程,特别注意对意外发 现、点滴收获、以及因个别疏漏而及时补充的方法等方面的内容进行撰写

概率论与数理统计课程教案 1 《概率论与数理统计》课程教案 主讲教师 所在单位 授课班级 专业 撰写时间 教案编号19-0703 教案内容7.4区间估计 学时1 基本要求 (1)了解区间估计、置信区间的概念,能够表述区间估计的思想和方法 1.培养能力要求: d)掌握概率论和数理统计中的基本概念和性质并能够运用到复杂工程 教学目标 能力要求 问题的适当表述之中: b)能够根据试验或观察得到的数据来研究随机现象,运用参数估计和 假设检验等基本的统计方法,对客观规律性做出合理的估计和判断 以解决实际问题。 教学重点 分布参数的风间估计的概念、求解思想 教学难点 区间估计统计量的构造 教学方法提问、讨论、讲授、启发、示例、板书、PPT 工具仪器 多媒体教具、教材、教案、教学课件、考勤表、平时成绩登记表 教学安排 考勤、复习相关知识点、新课内容概述、组织教学、布置作业、课后小结 教学过程 教学组织、具体教学内容及教学方法、手段、时间分配及其它说明 0 注 第一部分:旧知识点复习和新课内容概述(5分钟) 板书, 对于一个待估参数,在测量或计算时,常不以得到近似值为满足,还需要估 回顾 计误差,即要求知道近似值的精确程度,亦即所求真值所在的范围. 设总体X,参数9为待估参数 1)选一个符合评选标准的合适的估计量:无偏的,有效的,相合的 2)点估计:得到参数8的一个近似值d PPT 3)区间估计:对于未知参数0,除了求出它的点估计日外,还希望估计出 个范围,并希望知道这个范围包含参数9真值的可信程度。 这个范围通常以区间形式给出,同时还给出该区间包含参数&真值的可信程 度。这种形式的估计称为区间估计,这样的区间称为置信区间 本节学习分布参数的区间估计的概念和求解思想。 第二部分:区间估计的相关概念(10分钟)
概率论与数理统计课程教案 1 《概率论与数理统计》课程教案 主讲教师_ 所在单位_ 授课班级_ 专业_ 撰写时间_ 教案编号 19-0703 教案内容 7.4 区间估计 学时 1 教学目标 基本要求 (1)了解区间估计、置信区间的概念,能够表述区间估计的思想和方法。 能力要求 1. 培养能力要求: a) 掌握概率论和数理统计中的基本概念和性质并能够运用到复杂工程 问题的适当表述之中; b) 能够根据试验或观察得到的数据来研究随机现象,运用参数估计和 假设检验等基本的统计方法,对客观规律性做出合理的估计和判断, 以解决实际问题。 教学重点 分布参数的区间估计的概念、求解思想 教学难点 区间估计统计量的构造 教学方法 提问、讨论、讲授、启发、示例、板书、PPT 工具仪器 多媒体教具、教材、教案、教学课件、考勤表、平时成绩登记表 教学安排 考勤、复习相关知识点、新课内容概述、组织教学、布置作业、课后小结 教学过程 教学组织、具体教学内容及教学方法、手段、时间分配及其它说明 备 注 第一部分:旧知识点复习和新课内容概述(5 分钟) 对于一个待估参数,在测量或计算时,常不以得到近似值为满足,还需要估 计误差,即要求知道近似值的精确程度,亦即所求真值所在的范围. 设总体 X,参数 θ 为待估参数 1)选一个符合评选标准的合适的估计量:无偏的,有效的,相合的 2)点估计:得到参数 θ 的一个近似值 ˆ 3)区间估计:对于未知参数 θ,除了求出它的点估计 ˆ 外,还希望估计出一 个范围,并希望知道这个范围包含参数 θ 真值的可信程度。 这个范围通常以区间形式给出,同时还给出该区间包含参数 θ 真值的可信程 度。这种形式的估计称为区间估计,这样的区间称为置信区间 本节学习分布参数的区间估计的概念和求解思想。 第二部分:区间估计的相关概念(10 分钟) 板书, 回顾 PPT

区间估计的两个要素:一个是区间,一个是置信水平 置信区间:设总体X的分布函数Fx:)含有一个未知参数9,0e⊙(⊙是9的可能的 取值范围),对于给定值a0<a<1,若由来自X的样本X1,X2,.,X确定的两个统计 量日=日(X,X2,.,X)和a=可K,X2,.,X日<),对于任意9e0满足 PH0(X1,X,.,Xk<(X,X2,.,Xl21-a, 则称随机区间(,)是9的置信水平为1一α的置信区间,旦和万分别称为置信水 平为1一a的双侧置信区间的置信下限和置信上限,1一a称为置信水平 说明: 当X是连续型随机变量时,对于给定的a,总是按要求P(0<0<}=1一α求出 置信区间。 当X是离散型随机变量时,对于给定的a,常常找不到区间(但,)使得P叫<0<a】 恰为1一a,此时去找区间(8,a)使得P{0<<0)至少为1一a,且尽可能的接近1一a。 含义:对于任何一个样本所确定的一个置信区间(但,),它包含待估参数真值的概 率为1一a,即该区间包含待估参数真值的可信程度为100(1一%,该值越大,越 有理由相信真值所在范围为,ō) 第三部分置信区间的计算方法(10分钟) 例1:设总体X一Nu,d,O2为已知,u为未知,设X,X2,.,X是来自X的样本, 求μ的置信水平为1一α的置信区间 解:置信区间由样本来确定,?是4的无偏估计,可由样本获得观察值,且F~ Nu,o2nl,所以 X=~N0,1 σ1分 它不依赖于任何未知参数,按标准正态分布的上α分位点的定义,有 ra +1- 即Px-g
2 区间估计的两个要素:一个是区间,一个是置信水平 置信区间:设总体 X 的分布函数 F(x;θ)含有一个未知参数 θ,θ Θ(Θ 是 θ 的可能的 取值范围),对于给定值 α(0<α<1),若由来自 X 的样本 X1,X2,.,Xn 确定的两个统计 量 = (X1,X2,.,Xn)和 = (X1,X2,.,Xn)( < ),对于任意 θ Θ 满足 P{ (X1,X2,.,Xn)< θ< (X1,X2,.,Xn)}1-α, 则称随机区间( , )是 θ 的置信水平为 1-α 的置信区间, 和 分别称为置信水 平为 1-α 的双侧置信区间的置信下限和置信上限,1-α 称为置信水平 说明: 当 X 是连续型随机变量时,对于给定的 α,总是按要求 P{ <θ< }=1-α 求出 置信区间。 当 X 是离散型随机变量时,对于给定的 α,常常找不到区间( , )使得 P{ <θ< } 恰为 1-α,此时去找区间( , )使得 P{ <θ< }至少为 1-α,且尽可能的接近 1-α。 含义:对于任何一个样本所确定的一个置信区间( , ),它包含待估参数真值的概 率为 1-α,即该区间包含待估参数真值的可信程度为 100(1-α)%,该值越大,越 有理由相信真值所在范围为( , ) 第三部分置信区间的计算方法(10 分钟) 例 1:设总体 X~N(μ,σ 2 ),σ 2为已知,μ 为未知,设 X1,X2,.,Xn是来自 X 的样本, 求 μ 的置信水平为 1-α 的置信区间 解:置信区间由样本来确定, X 是 μ 的无偏估计,可由样本获得观察值,且 X ~ N(μ,σ 2 /n),所以 n X /− ~N(0,1) 它不依赖于任何未知参数,按标准正态分布的上 α 分位点的定义,有 − / 2 / z n X P =1-α, 即 P{ X - / 2 z n <μ< X + / 2 z n }=1-α
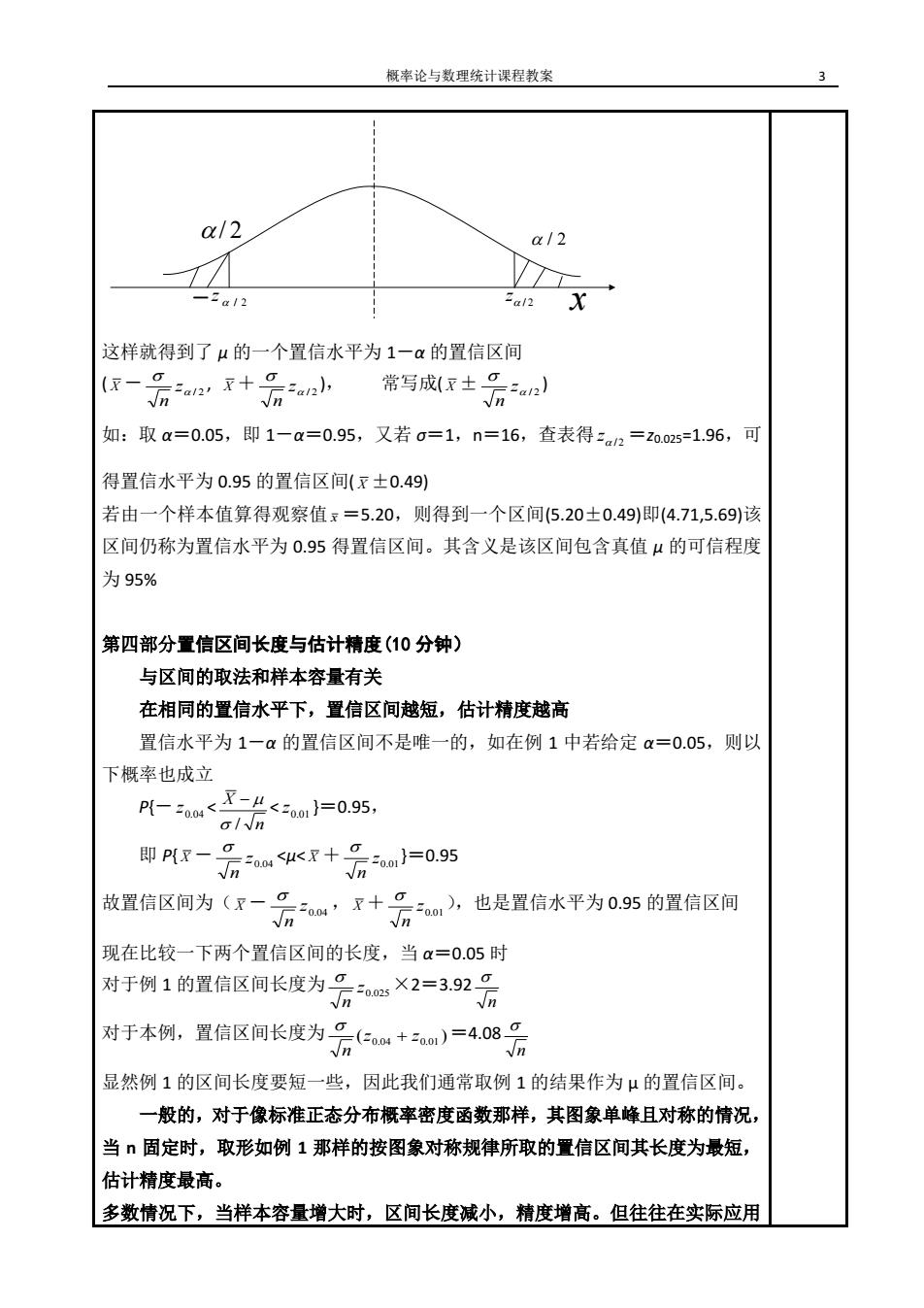
概率论与数理统计课程教案 a/2 a/2 V -2a12 这样就得到了μ的一个置信水平为1一α的置信区间 常写成x±号小 如:取a=0.05,即1-a=0.95,又若g=1,n=16,查表得:a2=z0.o2s=1.96,可 得置信水平为0.95的置信区间(x±0.49) 若由一个样本值算得观察值x=5.20,则得到一个区间(5.20士0.49)即(4.71,5.69)该 区间仍称为置信水平为0.95得置信区间。其含义是该区间包含真值4的可信程度 为95% 第四部分置信区间长度与估计精度(0分钟) 与区间的取法和样本容量有关 在相同的置信水平下,置信区间越短,估计精度越高 置信水平为1一α的置信区间不是唯一的,如在例1中若给定α=0.05,则以 下概率也成立 r-w=05, 4c8+05 即PT-g 故置信区同为(宝一子,+云人也是置信水平为095的置信区间 现在比较一下两个置信区间的长度,当a=0.05时 对于例1的置信区间长度为元X2=392号 对于本例、置信区同长度为云w+)=40号 显然例1的区间长度要短一些,因此我们通常取例1的结果作为μ的置信区间: 一般的,对于像标准正态分布概率密度函数那样,其图象单峰且对称的情况 当n固定时,取形如例1那样的按图象对称规律所取的置信区间其长度为最短, 估计精度最高。 多数情况下,当样本容量增大时,区间长度减小,精度增高。但往往在实际应用
概率论与数理统计课程教案 3 / 2 x z / 2 z / 2 / 2 - 这样就得到了 μ 的一个置信水平为 1-α 的置信区间 ( X - / 2 z n , X + / 2 z n ), 常写成( X ± / 2 z n ) 如:取 α=0.05,即 1-α=0.95,又若 σ=1,n=16,查表得 / 2 z =z0.025=1.96,可 得置信水平为 0.95 的置信区间( X ±0.49) 若由一个样本值算得观察值 x =5.20,则得到一个区间(5.20±0.49)即(4.71,5.69)该 区间仍称为置信水平为 0.95 得置信区间。其含义是该区间包含真值 μ 的可信程度 为 95% 第四部分置信区间长度与估计精度(10 分钟) 与区间的取法和样本容量有关 在相同的置信水平下,置信区间越短,估计精度越高 置信水平为 1-α 的置信区间不是唯一的,如在例 1 中若给定 α=0.05,则以 下概率也成立 P{- 0.04 z < n X /− < 0.01 z }=0.95, 即 P{ X - 0.04 z n <μ< X + 0.01 z n }=0.95 故置信区间为( X - 0.04 z n , X + 0.01 z n ),也是置信水平为 0.95 的置信区间 现在比较一下两个置信区间的长度,当 α=0.05 时 对于例 1 的置信区间长度为 0.025 z n ×2=3.92 n 对于本例,置信区间长度为 ( ) 0.04 0.01 z z n + =4.08 n 显然例 1 的区间长度要短一些,因此我们通常取例 1 的结果作为 μ 的置信区间。 一般的,对于像标准正态分布概率密度函数那样,其图象单峰且对称的情况, 当 n 固定时,取形如例 1 那样的按图象对称规律所取的置信区间其长度为最短, 估计精度最高。 多数情况下,当样本容量增大时,区间长度减小,精度增高。但往往在实际应用

中得到足够多的大量的样本是不实际的。 第五部分区间估计的一般方法(10分钟) 寻求未知参数9的置信区间的具体做法如下: 1°寻找样本X,X2,.,Xn的一个函数: W=WX1,X2,.,X:9l, 包含待估参数8,而不含其它未知参数,并且W的分布已知且不依赖于任何未知 参数(当然不依赖于待估参数):函数wX1,X2,.,X:)的构造常从日的点估计着手 考虑。 比如在例1中利用待估参数和相应估计量构造的一个标准正态分布函数 若No 2°对于给定的置信水平1一a,定出两个常数a,b,使得 Pla<W(X1Xz,-.,Xn;0)<b}21-a, 比1中PR气1e 注意这里尽量选取置信区间使其长度最短,以达到最佳估计精度 3°若能从不等式<wX,X,.,X,kb中得到等价的不等式<<,其中目 X,X,.,X,万=百X1,X2,.,X)都是统计量,那么(但,)就是9的一个置信水平 为1一x的置信区间。 例1中即P一n+=1-a 常用的正态总体参数置信区间可以用上述步骤推得 课后作业包括课后作业、数值实验作业、其它要求 课后小结是教案执行情况的经验总结,目的在于改进和调整教案,为下 课后小结 轮课讲授设计更加良好的教学方案。应全面审视教学过程,特别注意对意外发 现、点滴收获、以及因个别疏漏而及时补充的方法等方面的内容进行撰写
4 中得到足够多的大量的样本是不实际的。 第五部分区间估计的一般方法(10 分钟) 寻求未知参数 θ 的置信区间的具体做法如下: 1°寻找样本 X1,X2,.,Xn的一个函数: W=W(X1,X2,.,Xn; θ), 包含待估参数 θ,而不含其它未知参数,并且 W 的分布已知且不依赖于任何未知 参数(当然不依赖于待估参数 θ);函数 W(X1,X2,.,Xn; θ)的构造常从θ的点估计着手 考虑, 比如在例 1 中利用待估参数和相应估计量构造的一个标准正态分布函数 n X /− ~N(0,1) 2°对于给定的置信水平 1-α,定出两个常数 a,b,使得 P{a<W(X1,X2,.,Xn; θ)<b}1-α, 比如例 1 中 − / 2 / z n X P =1-α, 注意这里尽量选取置信区间使其长度最短,以达到最佳估计精度 3°若能从不等式 a<W(X1,X2,.,Xn; θ)<b 中得到等价的不等式 <θ< ,其中 = (X1,X2,.,Xn), = (X1,X2,.,Xn)都是统计量,那么( , )就是 θ 的一个置信水平 为 1-α 的置信区间。 例 1 中即 P{ X - / 2 z n <μ< X + / 2 z n }=1-α。 常用的正态总体参数置信区间可以用上述步骤推得。 课后作业 包括课后作业、数值实验作业、其它要求 课后小结 课后小结是教案执行情况的经验总结,目的在于改进和调整教案,为下一 轮课讲授设计更加良好的教学方案。应全面审视教学过程,特别注意对意外发 现、点滴收获、以及因个别疏漏而及时补充的方法等方面的内容进行撰写

薇率论与数理统计课程教案 1 《概率论与数理统计》课程教案 主讲教师 所在单位 授课班级 专业 撰写时间 教案编号20-0704 教案内容 ,5正态总体均值和方差的区间估计:7.6(0-1) 学时2 分布参数的区间估计:7.7单侧置信区间 (1)会求单个正态总体均值和方差的置信区间。 基本要求 (2)会求两个正态总体均值差和方差比的置信区间。 (3)了解(0-1)分布参数的区间估计,单侧置信区间的概念。 1.培养能力要求: 教学目标 )掌握概率论和数理统计中的基本概念和性质并能够运用到复杂工程 能力要求 问题的适当表述之中: b)能够根据试验或观察得到的数据来研究随机现象,运用参数估计和 设检验等基本的统计方法,对客观规律性做出合理的估计和判断,以 解决实际问题。 教学重点单个正态总体的均值和方差的置信区间,两个正态总体均值差与方差比的置信区间。 教学难点 区间估计统计量的构造 教学方法 提问、讲授、启发、示例、板书、PPT 工具仪器多媒体教具、教材、教案、教学课件、考勤表、平时成绩登记表 教学安排 考勤、复习相关知识点、新课内容概述、组织教学、布置作业、课后小结 教学过程教学组织、具体教学内容及教学方法、手段、时间分配及其它说明 备注 第一部分:旧知识点复习和新课内容概述5分钟) 板书,回 上一节我们学习了区间估计的基本概念和一般求解思路。 顾 寻求未知参数0的置信区间的具体做法如下: 1°寻找样本X,X2,.,X的一个函数: W=W(X1,X2,X), 包含待估参数8,而不含其它未知参数,并且W的分布己知且不依赖于任何未知 参数(当然不依赖于待估参数:函数WX1,X2,.,X,9)的构造常从日的点估计着手 考虑 2°对于给定的置信水平1一a,定出两个常数a,b,使得 P(a<W(X1Xz.-Xn;0)<b}21-a, 注意这里尽量选取置信区间使其长度最短,以达到最佳估计精度
概率论与数理统计课程教案 1 《概率论与数理统计》课程教案 主讲教师_ 所在单位_ 授课班级_ 专业_ 撰写时间_ 教案编号 20-0704 教案内容 7.5 正态总体均值和方差的区间估计;7.6 (0-1) 分布参数的区间估计;7.7 单侧置信区间 学时 2 教学目标 基本要求 (1)会求单个正态总体均值和方差的置信区间。 (2)会求两个正态总体均值差和方差比的置信区间。 (3)了解(0-1)分布参数的区间估计,单侧置信区间的概念。 能力要求 1. 培养能力要求: a) 掌握概率论和数理统计中的基本概念和性质并能够运用到复杂工程 问题的适当表述之中; b) 能够根据试验或观察得到的数据来研究随机现象,运用参数估计和假 设检验等基本的统计方法,对客观规律性做出合理的估计和判断,以 解决实际问题。 教学重点 单个正态总体的均值和方差的置信区间,两个正态总体均值差与方差比的置信区间。 教学难点 区间估计统计量的构造 教学方法 提问、讲授、启发、示例、板书、PPT 工具仪器 多媒体教具、教材、教案、教学课件、考勤表、平时成绩登记表 教学安排 考勤、复习相关知识点、新课内容概述、组织教学、布置作业、课后小结 教学过程 教学组织、具体教学内容及教学方法、手段、时间分配及其它说明 备 注 第一部分:旧知识点复习和新课内容概述(5 分钟) 上一节我们学习了区间估计的基本概念和一般求解思路。 寻求未知参数 θ 的置信区间的具体做法如下: 1°寻找样本 X1,X2,.,Xn的一个函数: W=W(X1,X2,.,Xn; θ), 包含待估参数 θ,而不含其它未知参数,并且 W 的分布已知且不依赖于任何未知 参数(当然不依赖于待估参数 θ);函数 W(X1,X2,.,Xn; θ)的构造常从θ的点估计着手 考虑, 2°对于给定的置信水平 1-α,定出两个常数 a,b,使得 P{a<W(X1,X2,.,Xn; θ)<b}1-α, 注意这里尽量选取置信区间使其长度最短,以达到最佳估计精度。 板书,回 顾

3°若能从不等式a<WX,X2,X;b中得到等价的不等式<<百,其中 X,X2,.,X,百=石(,X2,.,X都是统计量,那么(,)就是0的一个置信水平 为1一x的置信区间。 在此基础上,本节学习单个正态总体N4,o2),两个正态总体Nu1,0),N2,02, PPT (0一1)分布参数的区间估计,单侧置信区间。 第二部分:单个正态总体的区间估计(30分钟) (1)单个正态总体Nu,d)的情况 设己给定置信水平1一a,并设X1,X2.,X为总体N山,0的样本.,分别是 样本均值和样本方差 1均值μ的置信区间 心为已如,由上节例1构法的函数岩栏即可得到置份区同(士名】 b)为未知,这样不能用上节例1,其中含有未知参数o。 考虑到S2是σ2的无偏估计, 由第六章定理一,二,三可知 然人后0”-X0-功,且两者独立 2 再由:分布的定义/心-)=in-) al n/a 即。用5=√S来代替 d tar(n) 右边的t分布不依赖于任何未知参数,而t分布的对称性易得如下区间 P-ra-a-小-
2 3°若能从不等式 a<W(X1,X2,.,Xn; θ)<b 中得到等价的不等式 <θ< ,其中 = (X1,X2,.,Xn), = (X1,X2,.,Xn)都是统计量,那么( , )就是 θ 的一个置信水平 为 1-α 的置信区间。 在此基础上,本节学习单个正态总体 N(μ,σ 2 ),两个正态总体 N(μ1,σ1 2 ),N(μ2,σ2 2 ), (0-1)分布参数的区间估计,单侧置信区间。 第二部分:单个正态总体的区间估计(30 分钟) (1) 单个正态总体 N(μ,σ 2 )的情况 设已给定置信水平 1-α,并设 X1,X2,.,Xn为总体 N(μ,σ 2 )的样本. X ,S 2分别是 样本均值和样本方差 1°均值 μ 的置信区间 (a) σ 2为已知,由上节例 1 构造的函数 n X /− 即可得到置信区间( X ± / 2 z n ) (b) σ 2为未知,这样不能用上节例 1,其中含有未知参数 σ。 考虑到 S 2 是 σ 2的无偏估计, 由第六章定理一,二,三可知 显然 n X /− ~N(0,1), 2 2 ( 1) n − S ~χ 2 (n-1),且两者独立, 再由 t 分布的定义 /( 1) ( 1) / 2 2 − − − n n S n X = S n X /− ~t(n-1) 即 σ 用 S= 2 S 来代替 O t h(t) α/2 tα/2(n) α/2 -tα/2(n) 右边的 t 分布不依赖于任何未知参数,而 t 分布的对称性易得如下区间 − − ( 1) / t / 2 n S n X P = − − − − ( 1) / ( 1) / 2 t / 2 n S n X P t n =1-α PPT