
第四章原子结构 [引言]化学变化是分子间原子的重新组合。要深入理 解化学反应的实质,掌握元素及其化合物的性质, 就必须了解原子的结构。 [方法]轻因重果,为我所用。 第一节原子结构的复杂性 一、星式原子模型 1897年发现电子; 1911年Rutherford根据a离子散射实验结果,提出星式 原子模型:
第四章 原子结构 [引言]化学变化是分子间原子的重新组合。要深入理 解化学反应的实质,掌握元素及其化合物的性质, 就必须了解原子的结构。 [方法] 轻因重果,为我所用。 第一节 原子结构的复杂性 一、星式原子模型 1897年发现电子; 1911年Rutherford根据α离子散射实验结果,提出星式 原子模型;

[评述]奠定了正确认识原子结构的基础;但根据电磁 学:原子将毁灭,所产生的光谱应为连续光谱。 光谱:光通过分光镜后形成的色带(谱线) 。 连续光谱:色带无明显的分界线,为连续波长光。 线状光谱:谱线是分立的,有明显的分界。 二、近代原子模型—玻尔理论 1、氢光谱 在可见光区有四条分立谱线:入=b×[n2/(n2-4)] v=R(1/n12-1/n22) 碱金属原子的光谱也有类似规律。 2、Bohr理论 要点:
[评述]奠定了正确认识原子结构的基础;但根据电磁 学:原子将毁灭,所产生的光谱应为连续光谱。 光谱:光通过分光镜后形成的色带(谱线)。 连续光谱:色带无明显的分界线,为连续波长光。 线状光谱:谱线是分立的,有明显的分界。 二、近代原子模型——玻尔理论 1、氢光谱 在可见光区有四条分立谱线;λ=b×[n2/(n2-4)] ν=R(1/n1 2 - 1/n2 2 ) 碱金属原子的光谱也有类似规律。 2、Bohr理论 要点:

①电子在符合量子化条件的轨道上绕核运动,这些轨 道称为稳定轨道,电子在稳定轨道上运动不释放能 量: ②轨道离核越远,能量越大; 关系式:E=-2.179×1018/n2 基态:电子尽可能处于能量最低轨道的状态: 激发态:获得能量,电子跃迁到能量高轨道的状态。 ③脱离供给能量体系,激发态不稳定,电子将从高能 级回到较低能级,以光子形式放出能量。 光子学说:△E=hv 对氢光谱及原子结构的解释。 [简评]是结构理论的重大突破,但对原子结构复杂性 仍认识不够
①电子在符合量子化条件的轨道上绕核运动,这些轨 道称为稳定轨道,电子在稳定轨道上运动不释放能 量; ②轨道离核越远,能量越大; 关系式:E=-2.179×1018/n 2 基态:电子尽可能处于能量最低轨道的状态; 激发态:获得能量,电子跃迁到能量高轨道的状态。 ③脱离供给能量体系,激发态不稳定,电子将从高能 级回到较低能级,以光子形式放出能量。 光子学说:△E=hν 对氢光谱及原子结构的解释。 [简评]是结构理论的重大突破,但对原子结构复杂性 仍认识不够

三、电子的波粒二象性 波动性:表征:波长、频率、衍射干涉等: 粒子性:速度、质量、动量等。 光子学说启发,法国de Broglie设想电子具有波动性。 很快被电子衍射实验所证实。 可见,高速运动的电子,在原子中的运动规律必然与 宏观物体不同。 测不准原理—Heisenberg △X△P≥h/2n 第二节核外电子状态的描述 原子轨道 Schrodinger方程 a2Ψ ∂2Ψ,a2Ψ 8π2m Ox2 ⊙2 z2 h2 (E-V)平
三、电子的波粒二象性 波动性:表征:波长、频率、衍射干涉等; 粒子性:速度、质量、动量等。 光子学说启发,法国de Broglie设想电子具有波动性。 很快被电子衍射实验所证实。 可见,高速运动的电子,在原子中的运动规律必然与 宏观物体不同。 测不准原理——Heisenberg △X·△P≥h/2π 第二节 核外电子状态的描述 一、原子轨道 Schrödinger方程 = − + + ( ) 8 2 2 2 2 2 2 2 2 E V h m x y z

[说明]①方程的解Ψ非具体数值,而是一函数关系: ②有很多数学解Ψ: ③须同时引入三个限制条件,即三个量子数,Ψ才具 有确定的物理意义;换句话说,一组量子数确定后, 对应唯一解Ψ和相应的能量确定,该电子的运动状 态确定。 1、原子轨道与波函数 每个特定解Ψnm表示电子运动的一稳定状态,借用 “轨道”名称,称Ψ为原子轨道。 2、量子数n、m一限制条件 ①取值规则(制约关系) n: 自然数; 0:≤n-1,即0,+1,+2.n-1; m:m≤C,即0,±1,±2.±l
[说明]①方程的解Ψ非具体数值,而是一函数关系; ②有很多数学解Ψ; ③须同时引入三个限制条件,即三个量子数, Ψ才具 有确定的物理意义;换句话说,一组量子数确定后, 对应唯一解Ψ和相应的能量确定,该电子的运动状 态确定。 1、原子轨道与波函数 每个特定解Ψnm表示电子运动的一稳定状态,借用 “轨道”名称,称Ψ为原子轨道。 2、量子数n、、m——限制条件 ①取值规则(制约关系) n:自然数; :≤ n-1,即0,+1,+2. n-1; m:|m|≤ ,即0,±1,±2 . ±

②一主量子数 意义:表示电子离核的远近(统计意义);是决定电 子能量的主要因素,常将决定的能量状态称为电子 层(主层) 。 ③0一角量子数 意义:确定原子轨道的形状,在多电子原子中是决定 电子能量的次要部分。称为电子亚层或能级。 能量关系: 单电子体系:仅由n决定; 多电子体系:由n和共同决定。 ④m一磁量子数 意义:决定原子轨道在空间的伸展方向,不影响电子 能量
②n——主量子数 意义:表示电子离核的远近(统计意义);是决定电 子能量的主要因素,常将n决定的能量状态称为电子 层(主层)。 ③——角量子数 意义:确定原子轨道的形状,在多电子原子中是决定 电子能量的次要部分。称为电子亚层或能级。 能量关系: 单电子体系:仅由n决定; 多电子体系:由n和共同决定。 ④m——磁量子数 意义:决定原子轨道在空间的伸展方向,不影响电子 能量
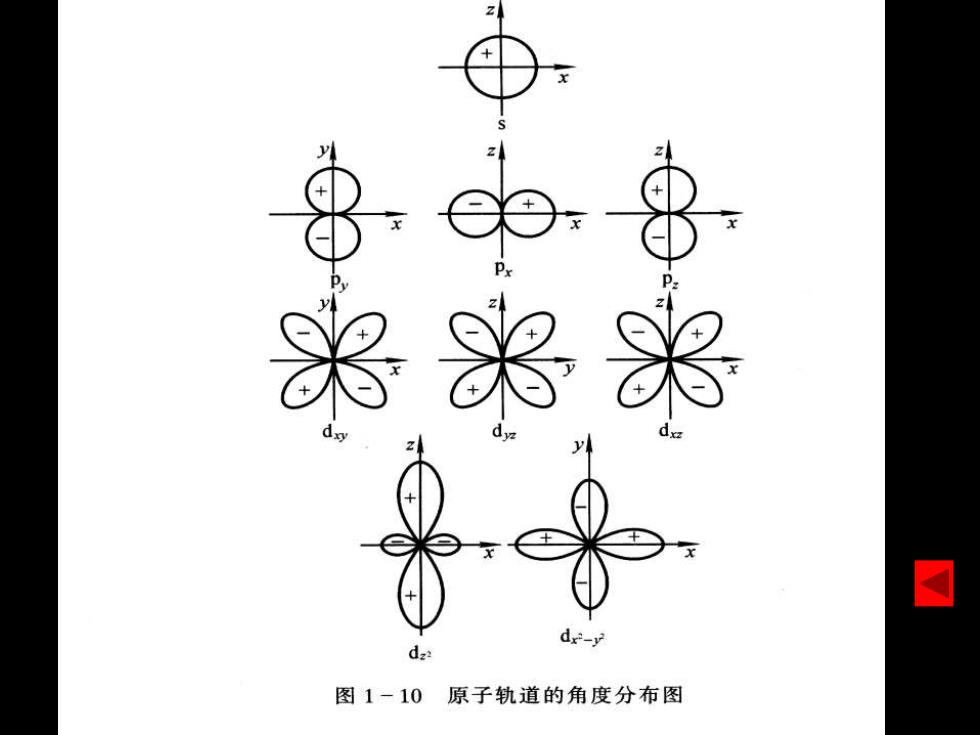
米米 de-y d2 图1-10原子轨道的角度分布图

2P2 s原子轨道伸展方向 3dx2y2 3 3dx 3d,2
s 原子轨道伸展方向

[说明]工、简并轨道一能量相同的轨道: Ⅱ、m有几个值,就有几个轨道。 二、电子云一统计观点 形象说明原子轨道。 1、几率:电子在空间出现的机会: 2、几率密度:电子在空间单位体积出现的机会。 根据电子衍射现象,几率密度等于Ψ2 3、电子云:用小黑点的疏密表示空间各处电子几率 密度大小,得到的图形。 三、自旋量子数ms 意义:表征电子的自旋情况,取值士1/2
[说明]Ⅰ、简并轨道——能量相同的轨道; Ⅱ、m有几个值,就有几个轨道。 二、电子云——统计观点 形象说明原子轨道。 1、几率:电子在空间出现的机会; 2、几率密度:电子在空间单位体积出现的机会。 根据电子衍射现象,几率密度等于|Ψ| 2 。 3、电子云:用小黑点的疏密表示空间各处电子几率 密度大小,得到的图形。 三、自旋量子数ms 意义:表征电子的自旋情况,取值±1/2

[小结]电子的运动状态需用一套四个量子数来描述, 缺一不可,即四个量子数确定后,电子在核外空间 的运动状态就确定了。 四、电子运动的可能状态数 [分析] 第三节核外电子排布和原子结构周期性 [前提]基态原子 一、排布原理 1.能量最低原理; 2.Paui不相容原理:原子中每个电子的一套量子数不允许 完全相同。 3.其他规则(后述) 二、能级顺序一近似能级图
[小结] 电子的运动状态需用一套四个量子数来描述, 缺一不可,即四个量子数确定后,电子在核外空间 的运动状态就确定了。 四、电子运动的可能状态数 [分析] 第三节 核外电子排布和原子结构周期性 [前提]基态原子 一、排布原理 1.能量最低原理; 2.Pauli不相容原理:原子中每个电子的一套量子数不允许 完全相同。 3.其他规则(后述) 二、能级顺序——近似能级图