
2 第十章 分类变量资料的统计分析 (1) 第一节 分类变量资料的统计描述 第二节 分类变量资料的统计推断 第三节 χ 2 检验
2 第十章 分类变量资料的统计分析 (1) 第一节 分类变量资料的统计描述 第二节 分类变量资料的统计推断 第三节 χ 2 检验

3 nomenclature rate 率 Overall rate 总体率 composition 成分 Raw number 原始数,实际数 constituent ratio 构成比 proportion 比例 Crude rate 粗率 Standardized rate 标准化率 Adjusted rate 调整率 ratio 比,比值 Direct standardization 直接标准化 indirect standardization 间接标准化 Standardized mortality ratio 标准化死亡率比
3 nomenclature rate 率 Overall rate 总体率 composition 成分 Raw number 原始数,实际数 constituent ratio 构成比 proportion 比例 Crude rate 粗率 Standardized rate 标准化率 Adjusted rate 调整率 ratio 比,比值 Direct standardization 直接标准化 indirect standardization 间接标准化 Standardized mortality ratio 标准化死亡率比

4 第一节 分类变量资料的统计描述 一、常用相对数:相对数是两个有关联的数值之比。 常用指标: (一) 率 (频率, 率). (二) 构成比 (三) 相对比 在调查或实验研究中,通过对分类变量资料进行清点而得 到的数据,称为实际数。实际数是研究客观事物本质的基 本信息,但不便于相互分析和比较,也不便于从中寻找事 物间的联系。因此,往往根据研究目的计算相应的相对数 指标,以便对资料进行统计学描述和深入的分析
4 第一节 分类变量资料的统计描述 一、常用相对数:相对数是两个有关联的数值之比。 常用指标: (一) 率 (频率, 率). (二) 构成比 (三) 相对比 在调查或实验研究中,通过对分类变量资料进行清点而得 到的数据,称为实际数。实际数是研究客观事物本质的基 本信息,但不便于相互分析和比较,也不便于从中寻找事 物间的联系。因此,往往根据研究目的计算相应的相对数 指标,以便对资料进行统计学描述和深入的分析

5 (一) 率(rate): 某现象实际发生数与该现象可能发生的总 数之比。用来说明某现象发生的频率或强度。常以百分率、 千分率、万分率或十万分率表示。原则上使计算结果至少 保留1位整数。 = − K (10 1) 实际发生某现象的观察数 率 可能发生该现象的观察单位总数 K为比例基数,通常取值为100%,1000‰,万/万, 十万/十万,等
5 (一) 率(rate): 某现象实际发生数与该现象可能发生的总 数之比。用来说明某现象发生的频率或强度。常以百分率、 千分率、万分率或十万分率表示。原则上使计算结果至少 保留1位整数。 = − K (10 1) 实际发生某现象的观察数 率 可能发生该现象的观察单位总数 K为比例基数,通常取值为100%,1000‰,万/万, 十万/十万,等
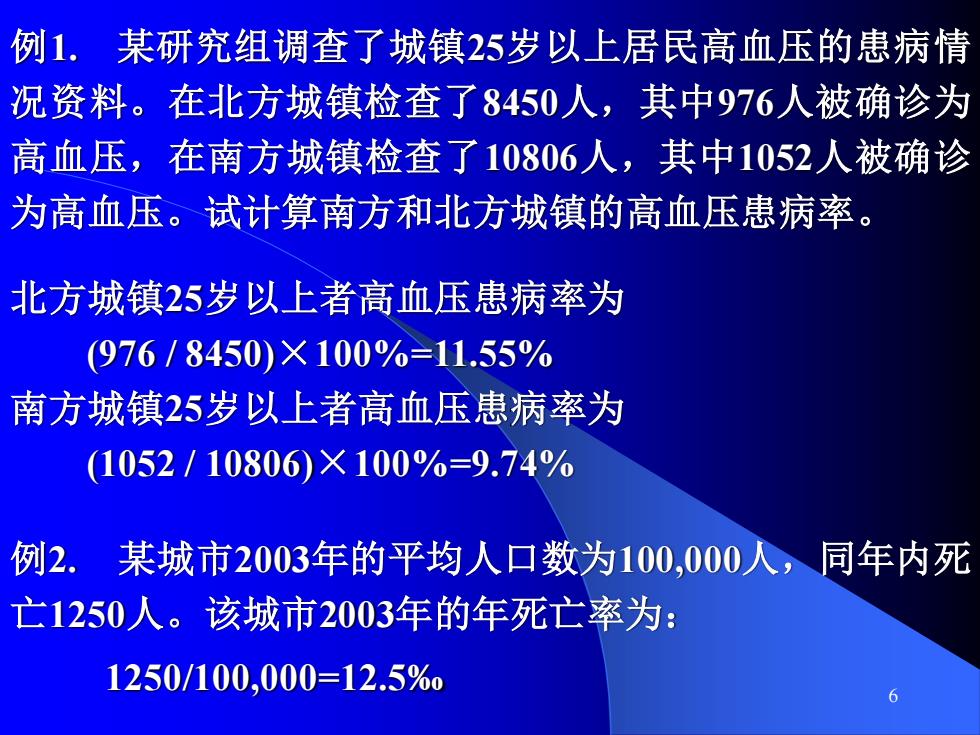
6 例1. 某研究组调查了城镇25岁以上居民高血压的患病情 况资料。在北方城镇检查了8450人,其中976人被确诊为 高血压,在南方城镇检查了10806人,其中1052人被确诊 为高血压。试计算南方和北方城镇的高血压患病率。 北方城镇25岁以上者高血压患病率为 (976 / 8450)×100%=11.55% 南方城镇25岁以上者高血压患病率为 (1052 / 10806)×100%=9.74% 例2. 某城市2003年的平均人口数为100,000人,同年内死 亡1250人。该城市2003年的年死亡率为: 1250/100,000=12.5‰
6 例1. 某研究组调查了城镇25岁以上居民高血压的患病情 况资料。在北方城镇检查了8450人,其中976人被确诊为 高血压,在南方城镇检查了10806人,其中1052人被确诊 为高血压。试计算南方和北方城镇的高血压患病率。 北方城镇25岁以上者高血压患病率为 (976 / 8450)×100%=11.55% 南方城镇25岁以上者高血压患病率为 (1052 / 10806)×100%=9.74% 例2. 某城市2003年的平均人口数为100,000人,同年内死 亡1250人。该城市2003年的年死亡率为: 1250/100,000=12.5‰

7 频率(relative frequency): 是一段时间时间的累计值, 强度(density):是单位时间的指标,是有时间单位的. 是强度或速率(rate)性质的指标.以年为时间的观察单位. 该城市2003年的年死亡率(12.5‰): 高血压患病率(北方城镇11.55%,南方城镇9.74%): 是频率性指标. 因为高血压患病人是长期累计的结果
7 频率(relative frequency): 是一段时间时间的累计值, 强度(density):是单位时间的指标,是有时间单位的. 是强度或速率(rate)性质的指标.以年为时间的观察单位. 该城市2003年的年死亡率(12.5‰): 高血压患病率(北方城镇11.55%,南方城镇9.74%): 是频率性指标. 因为高血压患病人是长期累计的结果
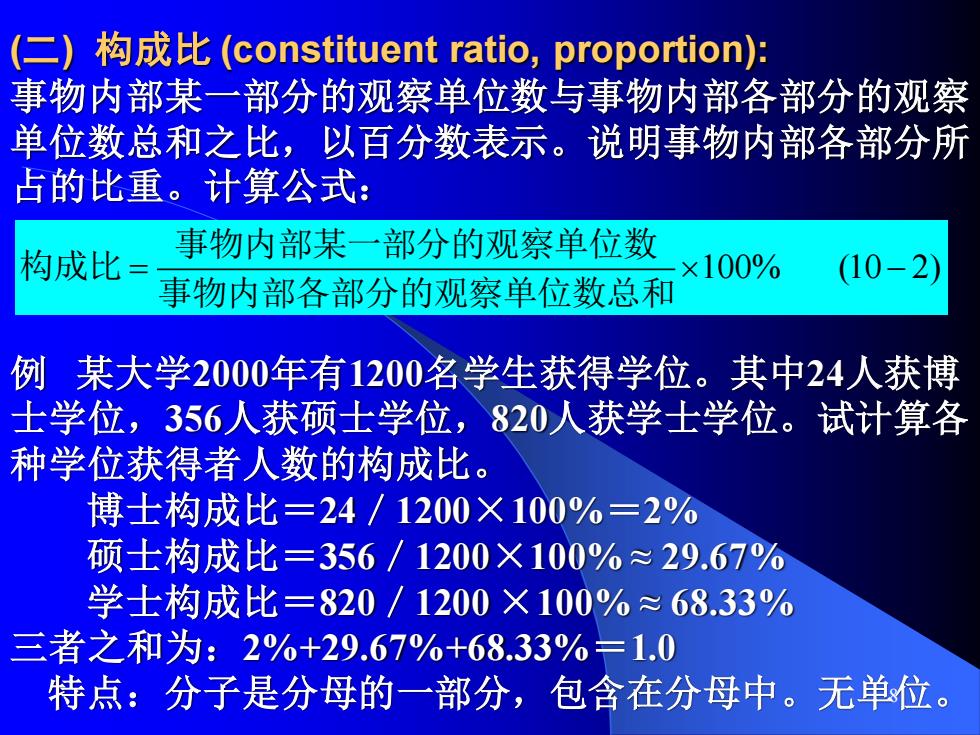
8 (二) 构成比 (constituent ratio, proportion): 事物内部某一部分的观察单位数与事物内部各部分的观察 单位数总和之比,以百分数表示。说明事物内部各部分所 占的比重。计算公式: = − 100% (10 2) 事物内部某一部分的观察单位数 构成比 事物内部各部分的观察单位数总和 例 某大学2000年有1200名学生获得学位。其中24人获博 士学位,356人获硕士学位,820人获学士学位。试计算各 种学位获得者人数的构成比。 博士构成比=24/1200×100%=2% 硕士构成比=356/1200×100% ≈ 29.67% 学士构成比=820/1200 ×100% ≈ 68.33% 三者之和为:2%+29.67%+68.33%=1.0 特点:分子是分母的一部分,包含在分母中。无单位
8 (二) 构成比 (constituent ratio, proportion): 事物内部某一部分的观察单位数与事物内部各部分的观察 单位数总和之比,以百分数表示。说明事物内部各部分所 占的比重。计算公式: = − 100% (10 2) 事物内部某一部分的观察单位数 构成比 事物内部各部分的观察单位数总和 例 某大学2000年有1200名学生获得学位。其中24人获博 士学位,356人获硕士学位,820人获学士学位。试计算各 种学位获得者人数的构成比。 博士构成比=24/1200×100%=2% 硕士构成比=356/1200×100% ≈ 29.67% 学士构成比=820/1200 ×100% ≈ 68.33% 三者之和为:2%+29.67%+68.33%=1.0 特点:分子是分母的一部分,包含在分母中。无单位

9 构成比的特点 (1) 各部分构成比之和等于1。 若因四舍五入造成构成比之和不等于1,则应进行适 当的调整,使其等于1。 (2) 当事物内部某一部分的构成比发生变化时,其它各部 分的构成比也会相应地发生变化。 该大学有240人获博士学位,356人获硕士学位,820人获 学士学位。 总人数为1416。获得各种学位人数的构成比: 博士构成比=240/1416×100%=16.95% (2%) 硕士构成比=356/1416×100%≈25.14% (29.67%) 学士构成比=820/1200 ×100%≈57.91% (68.33%) 一项的比例上升,引起其他比例的下降。反之亦然
9 构成比的特点 (1) 各部分构成比之和等于1。 若因四舍五入造成构成比之和不等于1,则应进行适 当的调整,使其等于1。 (2) 当事物内部某一部分的构成比发生变化时,其它各部 分的构成比也会相应地发生变化。 该大学有240人获博士学位,356人获硕士学位,820人获 学士学位。 总人数为1416。获得各种学位人数的构成比: 博士构成比=240/1416×100%=16.95% (2%) 硕士构成比=356/1416×100%≈25.14% (29.67%) 学士构成比=820/1200 ×100%≈57.91% (68.33%) 一项的比例上升,引起其他比例的下降。反之亦然

10 (三) 相对比(ratio): 即比值, 是两个有关指标之比,说明一 个指标是另一个指标的几倍或百分之几。 计算公式: 或 乙指标 甲指标 相对比 = = 100% 乙指标 甲指标 相对比 甲、乙两指标的性质可以相同也可以不同。 例如,反映一个国家人口结构的男女性别比、反映医院工 作效率的门诊人次数与床位数之比、反映人口密度的人口 数与土地面积之比等。 (10-3) 例10-2 门诊每次看病花费的时间大医院平均81.9分钟。 社区服务站平均18.6分钟。 平均每次看病花费的时间大医院与社区服务站之比为: 81.9分钟/ 18.6分钟=4.40(倍)
10 (三) 相对比(ratio): 即比值, 是两个有关指标之比,说明一 个指标是另一个指标的几倍或百分之几。 计算公式: 或 乙指标 甲指标 相对比 = = 100% 乙指标 甲指标 相对比 甲、乙两指标的性质可以相同也可以不同。 例如,反映一个国家人口结构的男女性别比、反映医院工 作效率的门诊人次数与床位数之比、反映人口密度的人口 数与土地面积之比等。 (10-3) 例10-2 门诊每次看病花费的时间大医院平均81.9分钟。 社区服务站平均18.6分钟。 平均每次看病花费的时间大医院与社区服务站之比为: 81.9分钟/ 18.6分钟=4.40(倍)
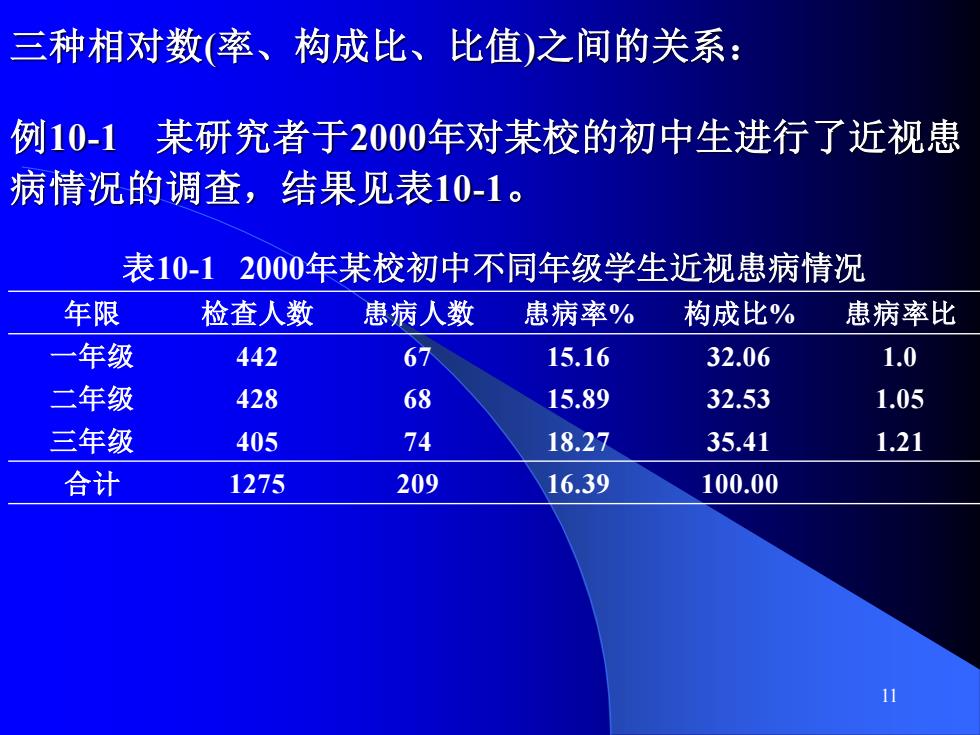
11 三种相对数(率、构成比、比值)之间的关系: 例10-1 某研究者于2000年对某校的初中生进行了近视患 病情况的调查,结果见表10-1。 表10-1 2000年某校初中不同年级学生近视患病情况 年限 检查人数 患病人数 患病率% 构成比% 患病率比 一年级 442 67 15.16 32.06 1.0 二年级 428 68 15.89 32.53 1.05 三年级 405 74 18.27 35.41 1.21 合计 1275 209 16.39 100.00
11 三种相对数(率、构成比、比值)之间的关系: 例10-1 某研究者于2000年对某校的初中生进行了近视患 病情况的调查,结果见表10-1。 表10-1 2000年某校初中不同年级学生近视患病情况 年限 检查人数 患病人数 患病率% 构成比% 患病率比 一年级 442 67 15.16 32.06 1.0 二年级 428 68 15.89 32.53 1.05 三年级 405 74 18.27 35.41 1.21 合计 1275 209 16.39 100.00