
2 第十一章 秩和检验 秩和检验是一种非参数统计。一般的统计 检验,都是在总体分布类型已知的条件下,对 其未知参数进行检验,通常这类统计称为参数 检验。但在实际情况下,总体分布不易判定, 这种不依赖总体分布,不受总体参数的影响, 它检验的是分布或分布位置,而不是参数。这 样的检验称为非参数检验
2 第十一章 秩和检验 秩和检验是一种非参数统计。一般的统计 检验,都是在总体分布类型已知的条件下,对 其未知参数进行检验,通常这类统计称为参数 检验。但在实际情况下,总体分布不易判定, 这种不依赖总体分布,不受总体参数的影响, 它检验的是分布或分布位置,而不是参数。这 样的检验称为非参数检验
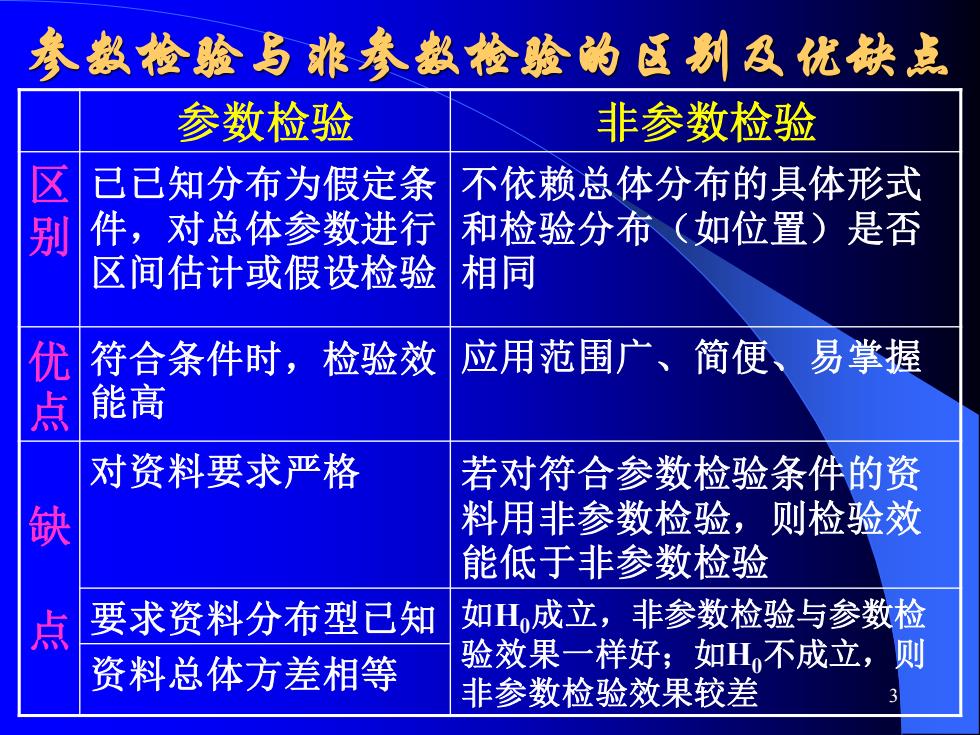
3 参数检验与非参数检验的区别及优缺点 参数检验 非参数检验 区 别 已已知分布为假定条 件,对总体参数进行 区间估计或假设检验 不依赖总体分布的具体形式 和检验分布(如位置)是否 相同 优 点 符合条件时,检验效 能高 应用范围广、简便、易掌握 缺 点 对资料要求严格 若对符合参数检验条件的资 料用非参数检验,则检验效 能低于非参数检验 要求资料分布型已知 如H0成立,非参数检验与参数检 验效果一样好;如H0不成立,则 资料总体方差相等 非参数检验效果较差
3 参数检验与非参数检验的区别及优缺点 参数检验 非参数检验 区 别 已已知分布为假定条 件,对总体参数进行 区间估计或假设检验 不依赖总体分布的具体形式 和检验分布(如位置)是否 相同 优 点 符合条件时,检验效 能高 应用范围广、简便、易掌握 缺 点 对资料要求严格 若对符合参数检验条件的资 料用非参数检验,则检验效 能低于非参数检验 要求资料分布型已知 如H0成立,非参数检验与参数检 验效果一样好;如H0不成立,则 资料总体方差相等 非参数检验效果较差

4 非参数检验适用范围 ⚫ 等级资料的比较。 ⚫ 偏态资料。 ⚫ 未知分布型资料。 ⚫ 要比较的各组资料变异度相差较大,方差不 齐, 且不能变换达到齐性。 ⚫ 初步分析 ⚫ 对于一些特殊情况,如从几个总体所获得的数 据,往往难以对其原有总体分布作出估计,在这 种情况下可用非参数统计方法
4 非参数检验适用范围 ⚫ 等级资料的比较。 ⚫ 偏态资料。 ⚫ 未知分布型资料。 ⚫ 要比较的各组资料变异度相差较大,方差不 齐, 且不能变换达到齐性。 ⚫ 初步分析 ⚫ 对于一些特殊情况,如从几个总体所获得的数 据,往往难以对其原有总体分布作出估计,在这 种情况下可用非参数统计方法

5 第一节 配对资料的符号秩和检验 (Wilcoxon配对 法) 配对设计: 1、同一批样品用两种不同的处理方法; 2、同一对子内不同的个体分别接受不同的处理。 3、在病因和危险因素的研究中,将病人和对照按 配对条件配成对子,研究是否存在某种病因或危 险因素
5 第一节 配对资料的符号秩和检验 (Wilcoxon配对 法) 配对设计: 1、同一批样品用两种不同的处理方法; 2、同一对子内不同的个体分别接受不同的处理。 3、在病因和危险因素的研究中,将病人和对照按 配对条件配成对子,研究是否存在某种病因或危 险因素

6 例11.1 某医院组织病人对护理质量 作评价,同时对护士进行再培训, 资料见表11.1中的⑵、⑶栏,问 培训前后的评分结果有无差别?
6 例11.1 某医院组织病人对护理质量 作评价,同时对护士进行再培训, 资料见表11.1中的⑵、⑶栏,问 培训前后的评分结果有无差别?

编号⑴ 培训前⑵ 培训后⑶ 差值d ⑷ 秩次⑸ 1 7 10 3 9 2 7 9 2 6.5 3 7 7 0 - 4 6 7 1 3 5 7 10 3 9 6 7 6 -1 -3 7 8 9 1 3 8 2 6 4 11 9 9 8 -1 -3 10 6 9 3 9 11 4 6 2 6.5 12 6 6 0 - 13 6 7 1 3 T+=60 T-=-6
编号⑴ 培训前⑵ 培训后⑶ 差值d ⑷ 秩次⑸ 1 7 10 3 9 2 7 9 2 6.5 3 7 7 0 - 4 6 7 1 3 5 7 10 3 9 6 7 6 -1 -3 7 8 9 1 3 8 2 6 4 11 9 9 8 -1 -3 10 6 9 3 9 11 4 6 2 6.5 12 6 6 0 - 13 6 7 1 3 T+=60 T-=-6

8 检验步骤: 1.建立假设,确立检验水准 注意: 在配对设计差值比较的符号秩和检验中, H0:两种方法测得的结果相同,即差值总体中位数为0 H1:两种方法测得的结果不同,即差值总体中位数不 等于0 α=0.05
8 检验步骤: 1.建立假设,确立检验水准 注意: 在配对设计差值比较的符号秩和检验中, H0:两种方法测得的结果相同,即差值总体中位数为0 H1:两种方法测得的结果不同,即差值总体中位数不 等于0 α=0.05

9 2.计算检验统计量 (1)求每对观察值的差数d; 如表11.1第(4)栏; (2)编秩 即按差值的绝对值从大到小编秩 ,并标明 原差值的正负号,如表11.1第(5)栏; 注意:编秩时,差数为0的略去不计,并相应减少对子 数n ; 编秩时,遇有差值的绝对值相等,符号相同, 顺序编秩;符号相反,取其平均秩次。 (3)求秩和 分别求正、负秩次之和,并以绝对值较 小者为统计量T值,如本例T-<T+,故T-=T
9 2.计算检验统计量 (1)求每对观察值的差数d; 如表11.1第(4)栏; (2)编秩 即按差值的绝对值从大到小编秩 ,并标明 原差值的正负号,如表11.1第(5)栏; 注意:编秩时,差数为0的略去不计,并相应减少对子 数n ; 编秩时,遇有差值的绝对值相等,符号相同, 顺序编秩;符号相反,取其平均秩次。 (3)求秩和 分别求正、负秩次之和,并以绝对值较 小者为统计量T值,如本例T-<T+,故T-=T

10 3.确定P值,做出推断结论 (1)查表法 当n≤50时,查T界值表(附表 9)(配对比较的秩和检验界值表),得P值, 按所取检验水准作出推断结论。 T值落在范围内,P> 界值P T值落在范围外,P< 界值P 本例n=13, T-=6,查附表T界值表(配对比较的符 号秩和检验用),T落在α=0.05的T界值范围外,按 α=0.05水准拒绝H0,接受H1。故可认为培训前后护理 质量评分有差别,培训后高于培训前,培训有利于提 高护理质量
10 3.确定P值,做出推断结论 (1)查表法 当n≤50时,查T界值表(附表 9)(配对比较的秩和检验界值表),得P值, 按所取检验水准作出推断结论。 T值落在范围内,P> 界值P T值落在范围外,P< 界值P 本例n=13, T-=6,查附表T界值表(配对比较的符 号秩和检验用),T落在α=0.05的T界值范围外,按 α=0.05水准拒绝H0,接受H1。故可认为培训前后护理 质量评分有差别,培训后高于培训前,培训有利于提 高护理质量

(2)正态近似法:如 n>50,可按下式正 态近似检验: ( 1)( 2 1) / 24 ( 1) / 4 0 .5 + + − + − = n n n T n n u 如果有相同秩次,应用下面的校正公式: ( ) 4 8 1 2 4 ( 1)(2 1) ( 1)/ 4 0.5 3 i i t t n n n T n n u − − + + − + − = 式中 ti为 第 i 个相同秩次的个数。如有相同秩次:3.5,3.5,6,6,6, 则∑(t 3 i-ti)=(23 -2)+(33 -3) 连续性校 正数 校正数
(2)正态近似法:如 n>50,可按下式正 态近似检验: ( 1)( 2 1) / 24 ( 1) / 4 0 .5 + + − + − = n n n T n n u 如果有相同秩次,应用下面的校正公式: ( ) 4 8 1 2 4 ( 1)(2 1) ( 1)/ 4 0.5 3 i i t t n n n T n n u − − + + − + − = 式中 ti为 第 i 个相同秩次的个数。如有相同秩次:3.5,3.5,6,6,6, 则∑(t 3 i-ti)=(23 -2)+(33 -3) 连续性校 正数 校正数