
实验十稀溶液粘度法测定聚合物的分子量 一、实验目的 1.了解聚合物分子量的统计平均意义: 2.掌握稀溶液粘度法表征聚合物分子量的基本原理: 3.。掌握测定聚合物稀溶液相对粘度的实验技术,包括搭建恒温槽装置: 4.通过对聚乙二醇水溶液相对粘度的测定表征聚乙二醇的粘均分子量。 二、基本原理 测定聚合物分子量的方法很多。各种方法都有它的优缺点和适用的分子量范围,由不同 方法得到的分子量的统计平均意义也不一样(表1)。 表常用测定分子量的方法及其大致适用范围 测定方法 适用的分子量范围 平均分子量 端基分析法 5×103 数均分子量 光散射法 >102 重均分子量 稀溶液粘度法 >102 粘均分子量 体积排斥色谱法 >102 各种平均分子量 采用稀溶液粘度法测定聚合物的分子量,所用仪器设备简单,操作便利,适用的分子量 范围大,又有相当好的实验精确度,因此粘度法是一种目前广泛应用的测定聚合物分子量的 方法。但它不是一种测定分子量的绝对方法,而是一 种相对方法,因为特性粘数一分子量经验关系式是要 用分子量绝对测定方法来校正订定的,本方法也就适 用于各种分子量范围。需注意的是在不同分子量范围 里,可能要用不同的经验方程式。 液体的流动是因受外力作用分子进行不可逆位移 的过程。液体分子间存在者相互作用力,因此当液体 图1液体的流动示意图
1 实验十 稀溶液粘度法测定聚合物的分子量 一、实验目的 1. 了解聚合物分子量的统计平均意义; 2. 掌握稀溶液粘度法表征聚合物分子量的基本原理; 3. 掌握测定聚合物稀溶液相对粘度的实验技术,包括搭建恒温槽装置; 4. 通过对聚乙二醇-水溶液相对粘度的测定表征聚乙二醇的粘均分子量。 二、基本原理 测定聚合物分子量的方法很多。各种方法都有它的优缺点和适用的分子量范围,由不同 方法得到的分子量的统计平均意义也不一样(表 1)。 表 1 常用测定分子量的方法及其大致适用范围 测定方法 适用的分子量范围 平均分子量 端基分析法 4 3 10 数均分子量 沸点升高法 4 3 10 数均分子量 冰点降低法 4 3 10 数均分子量 气相渗透压法 4 3 10 数均分子量 膜平衡渗透压法 3 6 5 10 10 数均分子量 电子显微镜法 5 5 10 数均分子量 光散射法 2 10 重均分子量 稀溶液粘度法 2 10 粘均分子量 体积排斥色谱法 2 10 各种平均分子量 采用稀溶液粘度法测定聚合物的分子量,所用仪器设备简单,操作便利,适用的分子量 范围大,又有相当好的实验精确度,因此粘度法是一种目前广泛应用的测定聚合物分子量的 方法。但它不是一种测定分子量的绝对方法,而是一 种相对方法,因为特性粘数-分子量经验关系式是要 用分子量绝对测定方法来校正订定的,本方法也就适 用于各种分子量范围。需注意的是在不同分子量范围 里,可能要用不同的经验方程式。 液体的流动是因受外力作用分子进行不可逆位移 的过程。液体分子间存在着相互作用力,因此当液体 v+dv v dz A A 图 1 液体的流动示意图

流动时,分子间就产生反抗其相对位移的摩擦力(内摩擦),液体的粘度就是液体分子间 这种内摩擦力的表现。 依照Newton的粘性流动定律,当两层流动液体面间(设面积为A)由于液体分子间的 内宰精产生流速梯安时(国液体对流功的性力是 (1) 刀就是液体的粘度,单位是帕斯卡秒。 当液体在半径为R、长度为L的毛细管里流动时(图 2),如果在毛细管两端间的压力差为P,并且假使促进液 体流动的力(πRP)全部用以克服液体对流动的粘性阻 力。那么在离轴r和(r+)的两圆柱面间的流动服从 下列方程式: rp42山-0 (2) 式(2)就规定了液体在毛细管里流动时的流速分布v(~)。 假如液体可以润湿管壁,管壁与液体间没有滑动,则 v(R=0,那么 图2液体在手细管流动示煮图 -, (3) 所以平均流出容速(设在1秒内流出液体的体积是V)是 片-2m-(R-rh- 8Ln (49 则液体的粘度可表示为 器 液体粘度的绝对值测定是很困难的,所以一般应用都测定相对粘度。在用稀溶液粘度法 表征高聚物分子量时,也只要测定不同浓度(C)稀溶液的相对粘度。 若以表示线剂的粘度,?表示的贴度,则溶的加时粘度为一只离分 溶液的粘度一般都比纯溶剂的粘度要大一些,溶液粘度增加的分数为溶液的增比粘度 2
2 流动时,分子间就产生反抗其相对位移的摩擦力(内摩擦力),液体的粘度就是液体分子间 这种内摩擦力的表现。 依照 Newton 的粘性流动定律,当两层流动液体面间(设面积为 A)由于液体分子间的 内摩擦产生流速梯度 v z 时(图 1),液体对流动的粘性阻力是 v f A z = (1) 就是液体的粘度,单位是帕斯卡·秒。 当液体在半径为 R 、长度为 L 的毛细管里流动时(图 2),如果在毛细管两端间的压力差为 P ,并且假使促进液 体流动的力( R P 2 )全部用以克服液体对流动的粘性阻 力。那么在离轴 r 和( r +dr )的两圆柱面间的流动服从 下列方程式: 2 2 0 dv r P rL dr + = (2) 式(2)就规定了液体在毛细管里流动时的流速分布 v r( ) 。 假如液体可以润湿管壁,管壁与液体间没有滑动,则 v R( ) = 0 ,那么 ( ) ( ) 2 2 2 4 r r R R dv P P v r dr rdr R r dr L L = = − = − (3) 所以平均流出容速(设在 t 秒内流出液体的体积是 V)是 ( ) 4 2 2 0 0 2 2 8 V P PR R R rvdr r R r dr t L L = = − = (4) 则液体的粘度可表示为 4 8 PR t LV = (5) 液体粘度的绝对值测定是很困难的,所以一般应用都测定相对粘度。在用稀溶液粘度法 表征高聚物分子量时,也只要测定不同浓度( C )稀溶液的相对粘度。 若以 0 表示纯溶剂的粘度, 表示溶液的粘度,则溶液的相对粘度为 0 r = 。高分子 溶液的粘度一般都比纯溶剂的粘度要大一些,溶液粘度增加的分数为溶液的增比粘度 图 2 液体在毛细管流动示意图 R r dr l
。=7=几-1。而二叫微比浓粘度,见叫微比浓对数转度,由于和见都 随溶液浓度改变而改变,而极稀溶液的相对粘度测定,不易准确,所以常用外推到C→0时 的二和卫值,这里,当浓度C不大时。 盟%-,+,2- (6 所以有 1m2=m2 令 lin -lim (8) 这个C→0时的外推值[]称为 高分子的特性粘数,其单位是为毫 升克或分升/克,与溶液浓度的单 位相对应。对于给定的体系,特性 粘数随分子量增加而增加,因此其 值可作为分子量的量度。 从溶液的比浓粘度2二和比 图3C-C图和Inn/C-C图 流对复错度之求取高分子的特性片数]写要有适合的结度与流度C的依款关系,适常 只有通过线性的外推,才能得到可靠的外推值。表达溶液粘度的浓度依赖性的经验方程式很 多,常用如下两个经验方程式,即Huggins方程式 (9 和Kraemer方程式: -Aope (10)
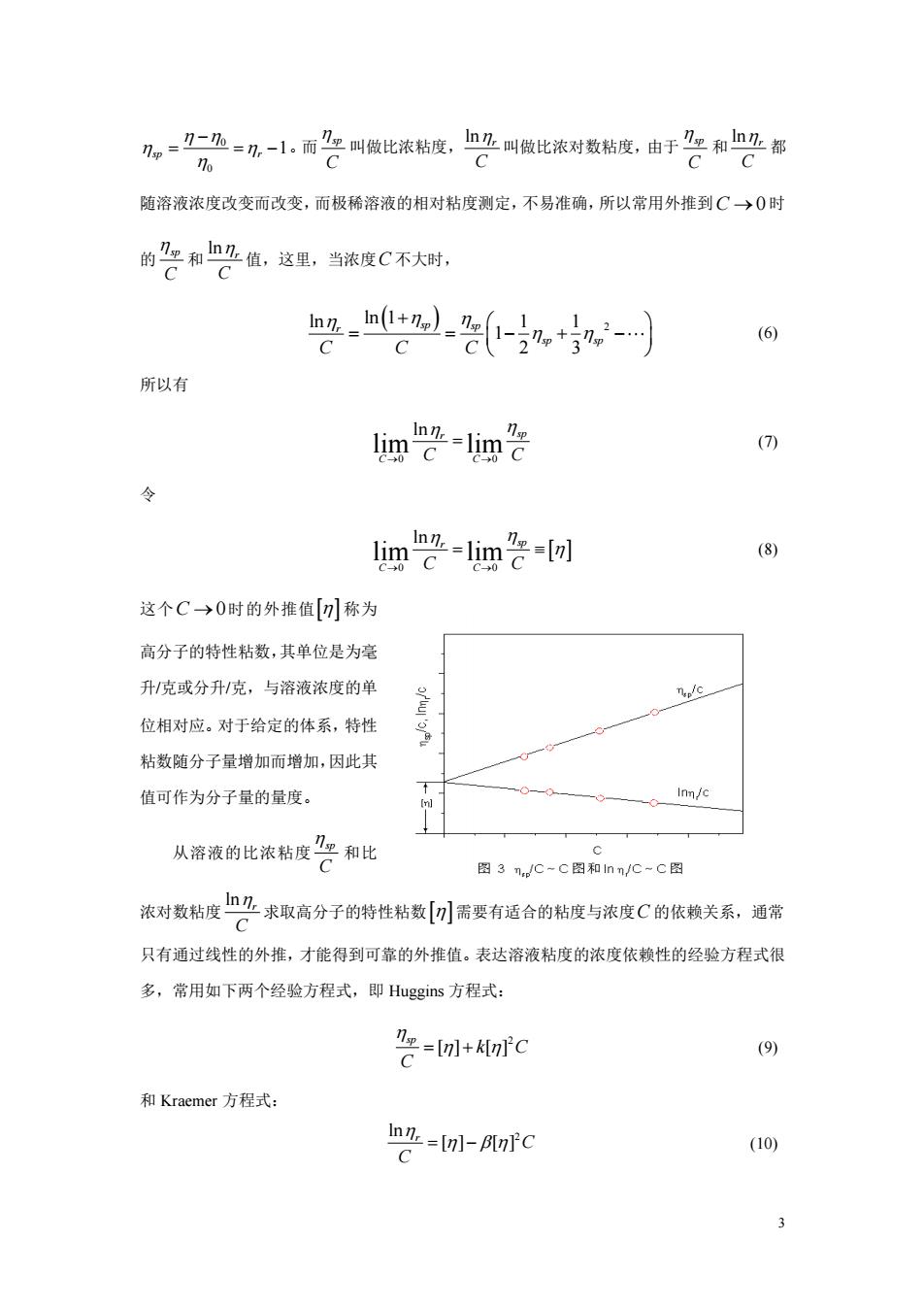
3 0 0 1 sp r − = = − 。而 sp C 叫做比浓粘度, ln r C 叫做比浓对数粘度,由于 sp C 和 ln r C 都 随溶液浓度改变而改变,而极稀溶液的相对粘度测定,不易准确,所以常用外推到 C →0 时 的 sp C 和 ln r C 值,这里,当浓度 C 不大时, ( ) 2 ln ln 1 1 1 1 2 3 r sp sp sp sp C C C + = = − + − (6) 所以有 0 0 ln lim lim r sp C C C C → → = (7) 令 0 0 ln lim lim r sp C C C C → → = (8) 这个 C →0 时的外推值 称为 高分子的特性粘数,其单位是为毫 升/克或分升/克,与溶液浓度的单 位相对应。对于给定的体系,特性 粘数随分子量增加而增加,因此其 值可作为分子量的量度。 从溶液的比浓粘度 sp C 和比 浓对数粘度 ln r C 求取高分子的特性粘数 需要有适合的粘度与浓度 C 的依赖关系,通常 只有通过线性的外推,才能得到可靠的外推值。表达溶液粘度的浓度依赖性的经验方程式很 多,常用如下两个经验方程式,即 Huggins 方程式: 2 [ ] [ ] sp k C C = + (9) 和 Kraemer 方程式: 2 ln [ ] [ ] r C C = − (10)

式(9、(10)中,k和B均为常数。按式(9、10)用=对C和血L对C作图,外推 到C→0所得的截距,应重合于一点,即[值(图3)。 需要注意的是,有的溶液比浓对数粘度与浓度的关系并不呈线性,尤其在浓度较高时, 发生偏离(向下弯曲或向上弯曲)。当出现这种情况时,建议使用式(9)求取[)]值。因为 式(9)、(10)均是通过对下式作近似处理而得到的, Inl (山 其中,k为常数。在推导式(9)时只作了一次近似处理,而推导式(10)时作了两次近似 处理。具体近似处理如下。 当]C1时,利用一级级数展开式(1-C)=1+C+,略去高次项, 代入式(11)即得式(9),大多数高分子稀溶液的比浓粘度与浓度的关系都符合式(9)。 当。写向上弯(<兮,曲线切线在外推到C一→0 所得的截距与2-C作图的直线在外推到C→0所得的截距将不重合于一点。这时最好 使用式(9),用空~C的作图的外推值求取[]值。 当确定了高分子的特性粘数[],就可根据特性粘数与分子量的关系式[)~M求取高 分子的分子量M。有时也直接用[]值来表示M的大小。 在早期工作中,人们就从理论上得出,特性粘数与分子量的关系式取决于高分子在溶液 中的形态。在溶液内高分子线团如果蜷得很紧,在流动时线团内的溶剂分子随着高分子一起 4
4 式(9)、(10)中,k 和 β 均为常数。按式(9)、(10)用 sp C 对 C 和 ln r C 对 C 作图,外推 到 C →0 所得的截距,应重合于一点,即 值(图 3)。 需要注意的是,有的溶液比浓对数粘度与浓度的关系并不呈线性,尤其在浓度较高时, 发生偏离(向下弯曲或向上弯曲)。当出现这种情况时,建议使用式(9)求取 值。因为 式(9)、(10)均是通过对下式作近似处理而得到的, [ ] 1 [ ] sp C k C = − (11) 其中,k 为常数。在推导式(9)时只作了一次近似处理,而推导式(10)时作了两次近似 处理。具体近似处理如下。 当 k C [ ] 1 时,利用一级级数展开式 ( ) 1 1 [ ] 1 [ ] k C k C − − = + + ,略去高次项, 代入式(11)即得式(9),大多数高分子稀溶液的比浓粘度与浓度的关系都符合式(9)。 当 1 sp 时, lnr 可按 Taylor 级数展开,即 ( ) 2 3 ln ln 1 2 3 sp sp r sp sp = + = − + + 把式(9)代入上式,略去高次项,得 2 3 2 ln 1 1 [ ] [ ] [ ] 2 3 r k C k C C = − − + − + (12) 若 1 3 k = ,且令 1 2 = − k ,则有式(10)。显然,若 1 3 k , ln r C C 的图形不再是 直线,当浓度较高时,曲线向下弯曲( 1 3 k )或向上弯曲( 1 3 k ),曲线切线在外推到 C →0 所得的截距与 sp C C 作图的直线在外推到 C →0 所得的截距将不重合于一点。这时最好 使用式(9),用 sp C C 的作图的外推值求取 值。 当确定了高分子的特性粘数 ,就可根据特性粘数与分子量的关系式 M 求取高 分子的分子量 M 。有时也直接用 值来表示 M 的大小。 在早期工作中,人们就从理论上得出,特性粘数与分子量的关系式取决于高分子在溶液 中的形态。在溶液内高分子线团如果蜷得很紧,在流动时线团内的溶剂分子随着高分子一起

流动,则高分子的特性粘数与分子量的平方根成正比,可xM2;假如线团松懈,在流 动时线团内的溶剂分子是完全自由的,那么高分子的特性粘数应与分子量成正比,xM。 目前常用一个包含两个参数的Mark-Houwink-Sakurada经验式表示特性粘数与分子量的关 系 [n]=KM (13) 式中,参数K、a值需经测定分子量的绝对方法订定后才可使用。订定方法是,先将高聚物 按分子量分级,测定各级分的特性粘数[和平均分子量M,以log[7]对logM作图,假 如a是常数,log[可小-logM的作图是直线,其斜率就是a,截距是logK。假如在实验的 分子量范围内,a不是常数,那么就从log[7]~logM作图的曲线上求取各段分子量范围 内适用的K、a值。对于常见的聚合物溶液体系,K、a值可以从有关手册或本教材附录 中查到。对于大部分高分子溶液来说,a的数值在0.51.0之间。 由于高分子的特性粘数和分子量的关系方程式[可]~M,视高分子在溶液里的形态而 异,而高分子的形态是高分子链段间和高分子一溶剂分子间相互作用力的反映,因此 [-M关系式随所用溶剂、测定温度不同而不同。根据Foy特性粘数方程式 @ [)]=0从,这里厅是高分子链的均方末端距,中是一个与高分子、溶剂以及温度无 关的通用常数。在日溶液中,高分子链单元间无远程相互作用,高分子尺寸恰好不受溶剂的 影响,线团处于一种无扰态,呈高斯无规线团形态,均方末端距h=(∝M,在这种情 况下,[]-M关系式可写成 [可]=KM (14) 如无规聚甲基丙烯酸甲酯一乙肺溶液在45℃(0温度)时,[)-M关系式为 [7]=0.048M0(ml/g),无规聚甲基丙烯酸甲酯-氯丁烷溶液在35.4℃(0温度)时, [)-M关系式为[=0.0505M0(mg)。而在其它情况下,F≠(,定义扩张因子 x=(居,则有
5 流动,则高分子的特性粘数与分子量的平方根成正比, 1/ 2 M ;假如线团松懈,在流 动时线团内的溶剂分子是完全自由的,那么高分子的特性粘数应与分子量成正比, M 。 目前常用一个包含两个参数的 Mark-Houwink-Sakurada 经验式表示特性粘数与分子量的关 系: a = KM (13) 式中,参数 K、a 值需经测定分子量的绝对方法订定后才可使用。订定方法是,先将高聚物 按分子量分级,测定各级分的特性粘数 和平均分子量 M ,以 log 对 log M 作图,假 如 a 是常数, log log M 的作图是直线,其斜率就是 a ,截距是 log K 。假如在实验的 分子量范围内, a 不是常数,那么就从 log log M 作图的曲线上求取各段分子量范围 内适用的 K 、 a 值。对于常见的聚合物溶液体系, K 、a 值可以从有关手册或本教材附录 中查到。对于大部分高分子溶液来说, a 的数值在 0.5~1.0 之间。 由于高分子的特性粘数和分子量的关系方程式 M ,视高分子在溶液里的形态而 异,而高分子的形态是高分子链段间和高分子―溶剂分子间相互作用力的反映,因此 M 关系式随所用溶剂、测定温度不同而不同。根据 Flory 特性粘数方程式 ( ) 3 2 2 h M = ,这里 2 h 是高分子链的均方末端距, 是一个与高分子、溶剂以及温度无 关的通用常数。在 θ 溶液中,高分子链单元间无远程相互作用,高分子尺寸恰好不受溶剂的 影响,线团处于一种无扰态,呈高斯无规线团形态,均方末端距 2 2 0 h h M = ,在这种情 况下, M 关系式可写成 1 2 = KM (14) 如无规聚 甲基丙 烯酸甲 酯—乙 腈溶液 在 45℃ (θ 温度 )时, M 关系式为 0.50 = 0.048M (ml/g),无规聚甲基丙烯酸甲酯—氯丁烷溶液在 35.4℃(θ 温度)时, M 关系式为 0.50 = 0.0505M (ml/g)。而在其它情况下, 2 2 0 h h ,定义扩张因子 ( ) 1 2 2 2 0 h h ,则有

M-M (15) 这里,?/M是常数,再根据F1ory导出的X-x2-2Cy(1-日/T)MP可知,x依赖 于M,因此[-M关系式仍可写成式(I3)的形式,其中的a值主要反映了x对M的 依赖性。如无规聚甲基丙烯酸甲酯一丙酮溶液在25℃(良溶剂条件)时,[]~M关系式 中a=0.69>0.50。这里高分子线团扩张,排除体积效应较大,这是由于良溶剂分子与高 分子链单元间的相互作用克服了链单元间的吸引力(高分子间的内聚力),溶剂的作用使同 一高分子链的链单元间呈现相斥的力。而当 溶剂变劣时,排斥体积则减小,线团收缩。 如25℃时无规聚甲基丙烯酸甲酯在乙腈和 氯丁烷中的a值分别为0.33和0.38,均小于 0.50. 注意:式(13)所表示的[可和M间的 函数形式,不能认为是有基础意义的,只能 看作是在一定分子量范围内,切和M间联 系关系的近似内插公式。在某些情况下,其 它函数形式可能更好地表达实验数据。如聚 环氧乙烷一水溶液在在25℃时,[)-M关 系式为[可=2.0+0.016,聚乙酸乙烯 酯一丙酮溶液在在30℃时,[)-M关系式为[可=0.097M0+0.007230。 测定高分子溶液的粘度以Ubbelohde式稀释粘度计最为合适(图4)。将液体自L管加 入,在M管将液体吸至E线以上后,任其流下,这样促使流动的力,就是液柱高h的压力, h值在k和:间逐渐改变,并且假设促使液体流动的力全部用于克服内摩擦力,即认为液 体在流动时没有消耗能量(一般选择纯溶剂流出时间大于100秒的粘度计,就可以略去流动 时能量损耗的主要部分一动能消耗的影响)。这样式(5)即为: 6
6 ( ) 3 2 2 2 3 2 2 0 0 1 2 3 h h M M M = = (15) 这里, 2 0 h M 是常数,再根据 Flory 导出的 ( ) 5 3 1 2 1 2 1 − = − C T M M 可知, 依赖 于 M ,因此 M 关系式仍可写成式(13)的形式,其中的 a 值主要反映了 对 M 的 依赖性。如无规聚甲基丙烯酸甲酯—丙酮溶液在 25℃(良溶剂条件)时, M 关系式 中 a = 0.69 0.50 。这里高分子线团扩张,排除体积效应较大,这是由于良溶剂分子与高 分子链单元间的相互作用克服了链单元间的吸引力(高分子间的内聚力),溶剂的作用使同 一高分子链的链单元间呈现相斥的力。而当 溶剂变劣时,排斥体积则减小,线团收缩。 如 25℃时无规聚甲基丙烯酸甲酯在乙腈和 氯丁烷中的 a 值分别为 0.33 和 0.38,均小于 0.50。 注意:式(13)所表示的 和 M 间的 函数形式,不能认为是有基础意义的,只能 看作是在一定分子量范围内, 和 M 间联 系关系的近似内插公式。在某些情况下,其 它函数形式可能更好地表达实验数据。如聚 环氧乙烷—水溶液在在 25℃时, M 关 系式为 0.76 = + 2.0 0.016M ,聚乙酸乙烯 酯—丙酮溶液在在 30℃时, M 关系式为 0.50 0.90 = + 0.097 0.00723 M M 。 测定高分子溶液的粘度以 Ubbelohde 式稀释粘度计最为合适(图 4)。将液体自 L 管加 入,在 M 管将液体吸至 E 线以上后,任其流下,这样促使流动的力,就是液柱高 h 的压力, h 值在 he 和 hf 间逐渐改变,并且假设促使液体流动的力全部用于克服内摩擦力,即认为液 体在流动时没有消耗能量(一般选择纯溶剂流出时间大于 100 秒的粘度计,就可以略去流动 时能量损耗的主要部分——动能消耗的影响)。这样式(5)即为:

n=zghpR't 8LV (16) 式中,g为重力加速度,h为流经毛细管的液柱的平均高度,P为所测液体的密度,1为液 面从a线流到b线所需的时间(流出时间。令A=严8R 8LΨ ,显然4是由粘度计所决定的 常数,与液体性质无关。则高分子溶液的粘度 n=Apr (17) 纯溶剂的粘度 (18 当测定的溶液很稀时,P≈P。,所以 (19) =儿-1片1 (20) 这样只要在同一温度下测定纯溶剂和不同浓度C的聚合物溶液流经a、b线的时间。和 1(、2、4、4)就可算出不同浓度溶液对溶剂的相对粘度,继而计算出p、n7 等,然后从2-C以及n2-C作图外推得到高分子的特性粘数[小,最后根据[-M 关系式求取聚合物分子量M。 因为需要测定不同浓度溶液的相对粘度,最简便且适用的方法是在粘度计里逐渐稀释 (详见操作步骤),可以节省许多操作手续,故采用气承悬液柱式的稀释粘度计最为合适, 因为液体的流出时间与粘度计中液体体积无关。 本实验是在同一支粘度计内测定一系列浓度成荷单比例关系的溶液的流出时间后,再测 溶剂的流出时间。这是因为考虑到高分子溶液流过毛细管后,常会有高分子吸附在毛细管管 壁,所以相当于高分子溶液流过了较细的毛细管,为了得到高分子溶液真实的相对粘度,后 测纯溶剂的流出时间,这样,纯溶剂流过的也是较细的毛细管,消除了高分子在毛细管上的
7 4 8 gh R t LV = (16) 式中, g 为重力加速度, h 为流经毛细管的液柱的平均高度, 为所测液体的密度, t 为液 面从 a 线流到 b 线所需的时间(流出时间),令 4 8 ghR A LV = ,显然 A 是由粘度计所决定的 常数,与液体性质无关。则高分子溶液的粘度 = At (17) 纯溶剂的粘度 0 0 0 = A t (18) 当测定的溶液很稀时, 0 ,所以 0 0 t t r = (19) 1 1 0 = − − t t sp r (20) 这样只要在同一温度下测定纯溶剂和不同浓度 C 的聚合物溶液流经 a、b 线的时间 0 t 和 t ( 1 t 、 2 t 、 3 t 、 4 t 、 5 t )就可算出不同浓度溶液对溶剂的相对粘度 r ,继而计算出 sp 、lnr 等,然后从 sp C C 以及 ln r C C 作图外推得到高分子的特性粘数 ,最后根据 M 关系式求取聚合物分子量 M 。 因为需要测定不同浓度溶液的相对粘度,最简便且适用的方法是在粘度计里逐渐稀释 (详见操作步骤),可以节省许多操作手续,故采用气承悬液柱式的稀释粘度计最为合适, 因为液体的流出时间与粘度计中液体体积无关。 本实验是在同一支粘度计内测定一系列浓度成简单比例关系的溶液的流出时间后,再测 溶剂的流出时间。这是因为考虑到高分子溶液流过毛细管后,常会有高分子吸附在毛细管管 壁,所以相当于高分子溶液流过了较细的毛细管,为了得到高分子溶液真实的相对粘度,后 测纯溶剂的流出时间,这样,纯溶剂流过的也是较细的毛细管,消除了高分子在毛细管上的

吸附对结果的影响。反之如果在测定溶液之前测定纯溶剂的流过时间,此时毛细管并未被高 分子吸附,纯溶剂将在较短的时间内流过毛细管,测定纯溶剂流过时间的毛细管状态就和之 后测定溶液流过时间时的状态不一致,如果高分子在毛细管管壁的吸附严重时,刀C一C的 作图将是一条凹形的曲线。 然而在有些情况下高分子在毛细管管壁的吸附还会引起界面性质的改变。如杨海洋发现 聚乙烯吡咯烷酮(PVP水溶液在极低浓度区的粘度行为是反常的,而这种反常行为不能简 单地被认为是由于高分子吸附在毛细管管壁上导致毛细管有效管径减小所致。这是由于玻璃 的表面是亲水的,而PVP是两亲性高分子,因此在测定PVP水溶液流过时间时,PVP的亲水 基团将优先吸附在毛细管管壁上,其憎水基团朝外,PVP分子在毛细管管壁上的吸附会使得 毛细管表面性质发生了显著改变,这样,流体在固体表面的张力也将因此而改变,界面性质 变化也会使流体在玻璃界面处接触角产生改变进而导致流体在流动过程中因弯曲液面而产 生的附加压强发生改变,最终影响到流体在粘度计中的流过时间。但是通过对粘度测定方法 进行改进也可消除界面性质变化的影响。杨海洋提出,以高分子溶液流过时间:对浓度作图, 外推到浓度为零时的流出时间6代替纯溶剂的流出时间1。来计算相对粘度。从测量的角度 上看,。可以被认为是理想条件下溶剂在粘度计中的流出时间。显然,这种方法不仅更加 省时省力、简单易行(免去了纯溶剂流过时间的测定),而且实验结果更为合理和普适。 对于多分散的聚合物,用式(13)计算所得的分子量是一种统计平均值。根据式(8) (13,有 limK (21) (p)e=KCM°=K∑C,M=KC∑ C 、M=KC∑(#M)(22) 而粘均分子量的定义式为 (23) 比较式(21)、(22)可知,采用稀溶液粘度法测得的是多分散聚合物的粘均分子量M, 而且其数值不仅与分子量分布有关,还与a值有关。 三、仪器和试剂 8
8 吸附对结果的影响。反之如果在测定溶液之前测定纯溶剂的流过时间,此时毛细管并未被高 分子吸附,纯溶剂将在较短的时间内流过毛细管,测定纯溶剂流过时间的毛细管状态就和之 后测定溶液流过时间时的状态不一致,如果高分子在毛细管管壁的吸附严重时, sp C C 的 作图将是一条凹形的曲线。 然而在有些情况下高分子在毛细管管壁的吸附还会引起界面性质的改变。如杨海洋发现 聚乙烯吡咯烷酮(PVP)-水溶液在极低浓度区的粘度行为是反常的,而这种反常行为不能简 单地被认为是由于高分子吸附在毛细管管壁上导致毛细管有效管径减小所致。这是由于玻璃 的表面是亲水的,而PVP是两亲性高分子,因此在测定PVP水溶液流过时间时,PVP的亲水 基团将优先吸附在毛细管管壁上,其憎水基团朝外,PVP分子在毛细管管壁上的吸附会使得 毛细管表面性质发生了显著改变,这样,流体在固体表面的张力也将因此而改变,界面性质 变化也会使流体在玻璃界面处接触角产生改变进而导致流体在流动过程中因弯曲液面而产 生的附加压强发生改变,最终影响到流体在粘度计中的流过时间。但是通过对粘度测定方法 进行改进也可消除界面性质变化的影响。杨海洋提出,以高分子溶液流过时间 t 对浓度作图, 外推到浓度为零时的流出时间 0 t 代替纯溶剂的流出时间 0 t 来计算相对粘度。从测量的角度 上看, * 0 t 可以被认为是理想条件下溶剂在粘度计中的流出时间。显然,这种方法不仅更加 省时省力、简单易行(免去了纯溶剂流过时间的测定),而且实验结果更为合理和普适。 对于多分散的聚合物,用式(13)计算所得的分子量是一种统计平均值。根据式(8)、 (13),有 0 lim sp a C KM C → = (21) ( ) ( ) 0 a a a a i sp i i i i i C i i i i i C KCM K C M KC M KC W M C → = = = = (22) 而粘均分子量的定义式为 1 a a i i i M W M = (23) 比较式(21)、(22)可知,采用稀溶液粘度法测得的是多分散聚合物的粘均分子量 M , 而且其数值不仅与分子量分布有关,还与 a 值有关。 三、仪器和试剂

乌式粘度计一支:恒温水梧一套(包括:电动搅拌器、继电器、水银接触温度计、调压 器、加热器、50℃温度计):秒表一块:5毫升、10毫升移液管各一支:25毫升、50毫升容 量瓶各一个:2或3“熔砂漏斗两个,50毫升烧杯等:聚乙二醇:蒸馏水。 四、操作步骤 1.玻璃仪器的洗涤 先用经熔砂漏斗滤过的水洗涤粘度计,倒挂干燥后,用新鲜温热的铬酸洗液(滤过)浸 泡粘度计数小时后,再用蒸馏水(经熔砂漏斗滤过的)洗净,干燥后待用。 其它如容量瓶、移液管也需经无尘洗涤、干燥后待用。 2.高分子溶液的配置 准确称取聚环乙二醇0.40.5克,在烧杯中用少量水(10-15毫升)使其全部溶解,移 入25毫升容量瓶中,用水洗涤烧杯3-4次,洗液一并转入容量瓶中,并稍稍摇晃作初步混 匀,然后将容量瓶置于恒温水槽(30C±0.05℃)中恒温,用水稀释至刻度,摇匀溶液,再 用熔砂漏斗将溶液滤入另一只25毫升的无尘干燥的容量瓶中,放入恒温水槽中恒温待用。 盛有无尘溶剂(也是经熔砂漏斗过滤过的)的容量瓶也放入恒温水槽中恒温待用。 3.溶液流出时间的测定 在粘度计的B、C管上小心地接入乳胶管,用固定夹夹住粘度计的A管,并将粘度计 垂直放入恒温水槽,使水面浸没:线上方的小球,用移液管从A管注入0毫升溶液,恒温 10分钟后,用乳胶管夹夹住C管上的乳胶管,在B管乳胶管上接上注射器,缓慢抽气,待 液面升到线上方的小球一半时停止抽气,先拔下注射器,而后放开C管的夹子,让空气 进入D球,使毛细管内溶液与A管下端的球分开,此时液面缓慢下降,用秒表记下液面从 a线流到b线的时间,重复测三次,每次所测的时间相差不超过02秒,取其平均值,作为1。 然后再移取5毫升溶剂注入粘度计,将它充分混合均匀,这时溶液浓度为原始溶液浓度 的23,再用同样方法测定12。 用同样操作方法再分别加入5、10和10毫升溶剂,使溶液浓度分别为原始溶液的12、 13和14,测定各自的流出时间4、1和1,。 4.纯溶剂流出时间的测定 将粘度计中的溶液倒出,用无尘溶剂(本实验中溶剂是水)洗涤粘度计数遍,测定纯溶 剂的流出时间1
9 乌式粘度计一支;恒温水槽一套(包括:电动搅拌器、继电器、水银接触温度计、调压 器、加热器、50℃温度计);秒表一块;5 毫升、10 毫升移液管各一支;25 毫升、50 毫升容 量瓶各一个;2 #或 3 #熔砂漏斗两个,50 毫升烧杯等;聚乙二醇;蒸馏水。 四、操作步骤 1. 玻璃仪器的洗涤 先用经熔砂漏斗滤过的水洗涤粘度计,倒挂干燥后,用新鲜温热的铬酸洗液(滤过)浸 泡粘度计数小时后,再用蒸馏水(经熔砂漏斗滤过的)洗净,干燥后待用。 其它如容量瓶、移液管也需经无尘洗涤、干燥后待用。 2. 高分子溶液的配置 准确称取聚环乙二醇 0.4~0.5 克,在烧杯中用少量水(10-15 毫升)使其全部溶解,移 入 25 毫升容量瓶中,用水洗涤烧杯 3-4 次,洗液一并转入容量瓶中,并稍稍摇晃作初步混 匀,然后将容量瓶置于恒温水槽(30℃±0.05℃)中恒温,用水稀释至刻度,摇匀溶液,再 用熔砂漏斗将溶液滤入另一只 25 毫升的无尘干燥的容量瓶中,放入恒温水槽中恒温待用。 盛有无尘溶剂(也是经熔砂漏斗过滤过的)的容量瓶也放入恒温水槽中恒温待用。 3. 溶液流出时间的测定 在粘度计的 B、C 管上小心地接入乳胶管,用固定夹夹住粘度计的 A 管,并将粘度计 垂直放入恒温水槽,使水面浸没 a 线上方的小球,用移液管从 A 管注入 10 毫升溶液,恒温 10 分钟后,用乳胶管夹夹住 C 管上的乳胶管,在 B 管乳胶管上接上注射器,缓慢抽气,待 液面升到 a 线上方的小球一半时停止抽气,先拔下注射器,而后放开 C 管的夹子,让空气 进入 D 球,使毛细管内溶液与 A 管下端的球分开,此时液面缓慢下降,用秒表记下液面从 a 线流到 b 线的时间,重复测三次,每次所测的时间相差不超过 0.2 秒,取其平均值,作为 1 t 。 然后再移取 5 毫升溶剂注入粘度计,将它充分混合均匀,这时溶液浓度为原始溶液浓度 的 2/3,再用同样方法测定 2 t 。 用同样操作方法再分别加入 5、10 和 10 毫升溶剂,使溶液浓度分别为原始溶液的 1/2、 1/3 和 1/4,测定各自的流出时间 3 t 、 4 t 和 5 t 。 4. 纯溶剂流出时间的测定 将粘度计中的溶液倒出,用无尘溶剂(本实验中溶剂是水)洗涤粘度计数遍,测定纯溶 剂的流出时间 0 t
五、数据记录和处理 粘度计号:一 毛细管内径: 温度: 。溶剂: 聚环氧乙烷重量: (克) 原始溶液浓度C。: _(克/毫升) 纯溶剂流出时间:() (秒)(2) (秒):(3) (秒) 取平均值。= (秒) 为作图方便,若原始溶液浓度为C。,稀释后溶液浓度为C,C=C,C”,C'为稀释后 溶液的相对浓度。那么原始溶液的相对浓度C"=1,依次加入5、5、10和10毫升溶剂的溶 液的相对浓度分别为23、12、1/3和14。 以np/C'和nn,/C'分别对C'作图,即 -+Cic' 图 na=miC。-nc8c (9 作图时可以在横坐标上以坐标纸的12格作为相对浓度C”=1,即原始溶液,则其它溶液就 位于8、6、4和3格处,外推得到截距A,A=[C。那么, 号 将得到的[)值代入[=KM,算出聚合物的粘均分子量M,=(/K)。 从Polymer Handbook查到:聚乙二醇-水溶液,在30℃时,K=0.0125m/g a=0.78. 加入溶剂的量相对浓度 流出时间(秒】 (毫升) 第一次第二次第三次平均值 e/C Inn./C (C') 0 2/3 2= 12 3= 10 13 14= 10 14
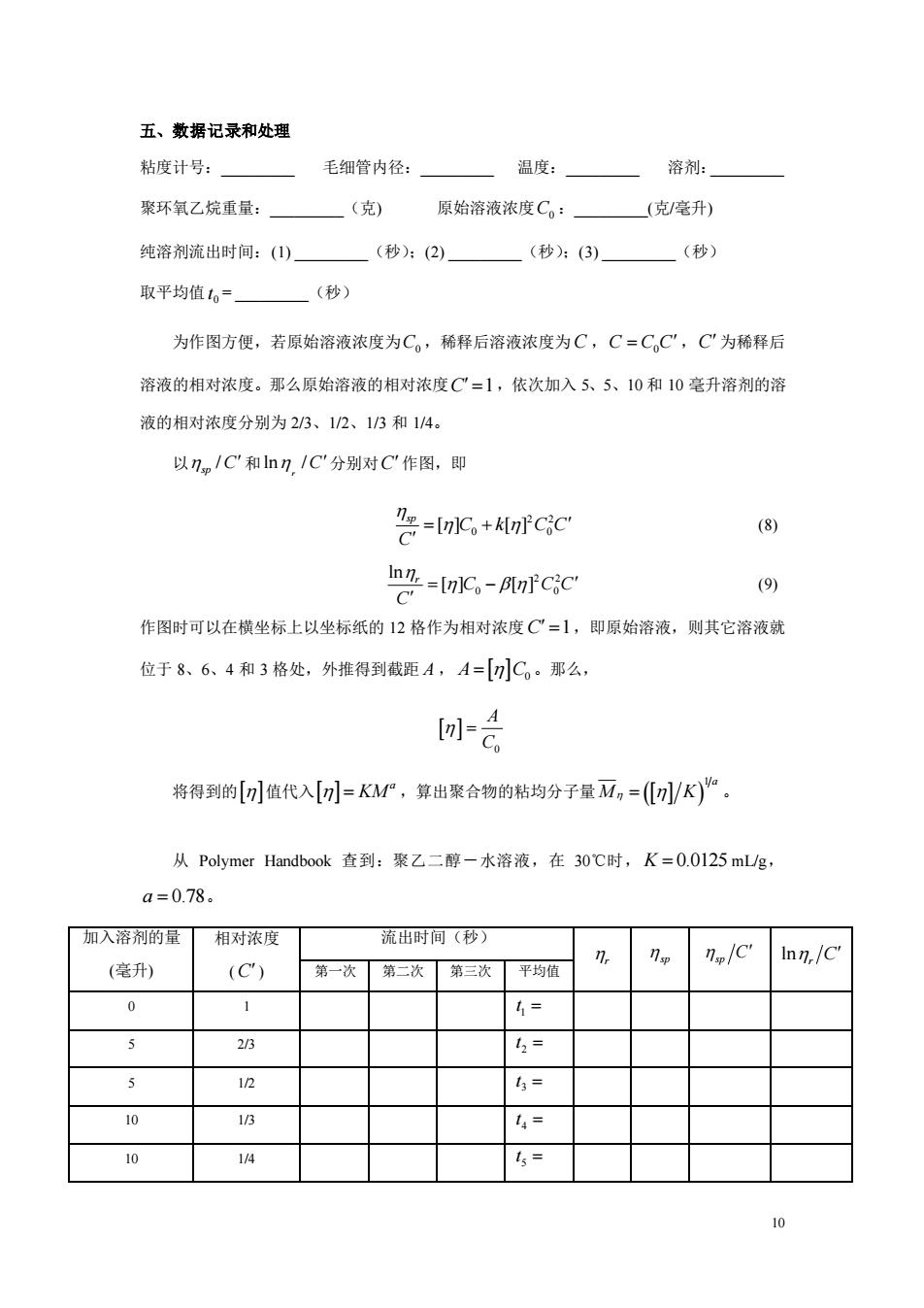
10 五、数据记录和处理 粘度计号:_ 毛细管内径:_ 温度:_ 溶剂:_ 聚环氧乙烷重量:_(克) 原始溶液浓度 C0 :_(克/毫升) 纯溶剂流出时间:(1) _(秒);(2) _(秒);(3) _(秒) 取平均值 0 t = _(秒) 为作图方便,若原始溶液浓度为 C0 ,稀释后溶液浓度为 C ,C C C0 = ,C 为稀释后 溶液的相对浓度。那么原始溶液的相对浓度 C =1,依次加入 5、5、10 和 10 毫升溶剂的溶 液的相对浓度分别为 2/3、1/2、1/3 和 1/4。 以 / sp C 和 ln / r C 分别对 C 作图,即 2 2 0 0 [ ] [ ] sp C k C C C = + (8) 2 2 0 0 ln [ ] [ ] r C C C C = − (9) 作图时可以在横坐标上以坐标纸的 12 格作为相对浓度 C =1 ,即原始溶液,则其它溶液就 位于 8、6、4 和 3 格处,外推得到截距 A , A C = 0 。那么, 0 A C = 将得到的 值代入 a = KM ,算出聚合物的粘均分子量 ( ) 1 a M K = 。 从 Polymer Handbook 查到:聚乙二醇-水溶液,在 30℃时, K = 0.0125 mL/g, a = 0.78。 加入溶剂的量 (毫升) 相对浓度 ( C ) 流出时间(秒) r sp sp C lnr C 第一次 第二次 第三次 平均值 0 1 1 t = 5 2/3 2 t = 5 1/2 3 t = 10 1/3 4 t = 10 1/4 5 t =