
第五讲:分子的对称性与群论基础 群表示与不可约表示
第五讲:分子的对称性与群论基础 群表示与不可约表示

群表示 1.群表示 1).群表示的定义 定义:若矩阵群ΓE,A,B,C,A} 是抽象群GE,AB,CA} 的一个同态映像,则厂称为G的一个矩阵表示。 [说明]: 口矩阵群的元素是同阶方阵; ▣ 矩阵群的运算规则:矩阵乘法: 口矩阵群的单位元为:单位矩阵; 口 由数字1构成的矩阵群是任何群G的一个同态映像,称全对 称表示。任何标量函数是全对称表示的基函数: 一个抽象群可以有无穷多个矩阵表示。 ftr)=fRr)
1. 群表示 2 定义:若矩阵群 是抽象群 的一个同态映像,则 G 称为G的一个矩阵表示。 GE,A,B,C, GE ˆ ,A ˆ ,B ˆ ,C ˆ [说明]: 矩阵群的元素是同阶方阵; 矩阵群的运算规则:矩阵乘法; 矩阵群的单位元为:单位矩阵; 由数字 1 构成的矩阵群是任何群G的一个同态映像,称全对 称表示。任何标量函数是全对称表示的基函数; 一个抽象群可以有无穷多个矩阵表示。 Rf r fR r 1 ˆ ˆ 群表示 1). 群表示的定义

群表示 2.群表示 2).等价表示与不等价表示 定义:如果群的表示下与下’的矩阵,以同一相似变换相 关联,则T与T为等价表示。 T:E,AB,C,. T:E',A',B',C,. 两者等价,是指满足下列关系: A'=P-AP,B'=P-BP,C"=P-CP,. P是一个非奇异方阵(P≠0),但不一定是群表示的矩阵。 3
2. 群表示 3 P 是一个非奇异方阵 ( ) ,但不一定是群表示的矩阵。 定义:如果群的表示 G 与 G’ 的矩阵,以同一相似变换相 关联,则 G 与 G’ 为等价表示。 G: E, A, B, C, . G': E', A', B', C', . A P AP, B' P B P, C' P CP, . 1 1 1 P 0 两者等价,是指满足下列关系: 群表示 2). 等价表示与不等价表示

群表示和不可约表示 1.群表示 示例: 选取基函数为: (f,)=x2-y2,2xy,x2+y2) 可以得到C3v点群6个对称操作的矩阵表示 (Γ1): 100 -1/2 5/20 -1/2 -5/2 0 E= 01 0 C,= 5/2 -1/2 0 C3= V3/2 -1/2 0 001 0 0 0 0 1 10 0 -1/2 5/2 0 -1/2 -3/20 Oy= 0 -1 0 3/2 1/2 0 -3/2 1/2 0 0 0 0 0 0
1. 群表示 4 选取基函数为: 可以得到 C3V 点群6个对称操作的矩阵表示 (G1 ): 2 2 2 2 1 2 3 f , f , f x y ,2xy, x y 0 0 1 0 1 0 1 0 0 E 0 0 1 3 2 1/ 2 0 1/ 2 3 2 0 C3 0 0 1 3 2 1/ 2 0 1/ 2 3 2 0 2 C3 0 0 1 0 1 0 1 0 0 σV 0 0 1 3 2 1/ 2 0 1/ 2 3 2 0 σV 0 0 1 3 2 1/ 2 0 1/ 2 3 2 0 σ V 示例: 群表示和不可约表示

群表示和不可约表示 1.群表示 选取基函数为: (g1,8283)=(x2,2xy,y2) 则可以得到C3V点群6个对称操作的矩阵表示如下(T2) 100 1/4 3/2 1 00 3/4 E=01 0 -1/2 √3/4 Oy= 0-10 001 3/4 -√3/2/4 01 (0 C=C,C3 Gy=GyC3 Gy=GyC 两组基函数有变换关系: 1/2 0-1/2 (x2,2xy,y2)=(x2-y2,2xy,x2+y2) 0 0 -1/201/2 即: 0 1/2 0-1 (g1,82,83)=(f,f5P1 1 P-1= 0 0 0 -1/20 1/2
1. 群表示 5 选取基函数为: 2 2 1 2 3 g , g , g x ,2xy, y 0 0 1 0 1 0 1 0 0 E 3 4 3 2 1 4 3 4 1/ 2 3 4 1/ 4 3 2 3/ 4 C3 0 0 1 0 1 0 1 0 0 σV 3 3 2 C3 C C σV σV C3 2 σV σV C3 则可以得到C3V点群6个对称操作的矩阵表示如下 (G2) : 两组基函数有变换关系: 1 1 2 3 1 2 3 , , , , g g g f f f P 即: 群表示和不可约表示 𝑥 2 , 2𝑥𝑦, 𝑦 2 = 𝑥 2 − 𝑦 2 , 2𝑥𝑦, 𝑥 2 + 𝑦 2 1/2 0 −1/2 0 1 0 −1/2 0 1/2 𝑃 −1 = 1/2 0 −1/2 0 1 0 −1/2 0 1/2 𝑃 = 1 0 1 0 1 0 −1 0 1

群表示和不可约表示 1.群表示 1/20-1/2 两组对称操作矩阵有变换关系: P= 01 0 RT2)=P-RTP /201/2 (101 C;T2)=P-C;TP 0 10 1/4 V3/2 3/4 0 1 1 -1/2 √3/201y2 0-1V2 3/4 -1/2 V5/4 0 1 0 √3/2 -1/2 0 0 10 3/4 -3/2 1/4 -10 0 /201/2 一个对称操作(算符)在同一个函数空间(x,y的二次齐次函数)的 作用效果,只是基函数的选取是不同的。可见,等价表示本质上是 “相同”的表示
1. 群表示 6 两组对称操作矩阵有变换关系: C Γ P C3 Γ1 P 1 3 2 1 2 0 1 2 0 1 0 1 2 0 1 2 0 0 1 3 2 1 2 0 1 2 3 2 0 1 0 1 0 1 0 1 0 1 3 4 3 2 1 4 3 4 1 2 3 4 1 4 3 2 3 4 RΓ P RΓ1 P 1 2 1 2 0 1 2 0 1 0 1 2 0 1 2 P 1 0 1 0 1 0 1 0 1 1 P 一个对称操作(算符)在同一个函数空间(x,y的二次齐次函数)的 作用效果,只是基函数的选取是不同的。可见,等价表示本质上是 “相同”的表示。 群表示和不可约表示
群表示和不可约表示 1.群表示 矩阵的迹(对角元之和): rA=∑4 相似变换不改变矩阵的迹(对角元素之和) 等价表示的相应矩阵的迹相同。即: 若: A'=P-AP, B'=P-BP. 则: TrA=TrA',TrB=TrB. 证明: Tr(ABC)=Tr(BCA) Σc=∑ΣΣa5a -∑∑∑b,a 故有:Tr(A)=TrP-AP)=P-PA)=Tr(A) =∑BCA)n
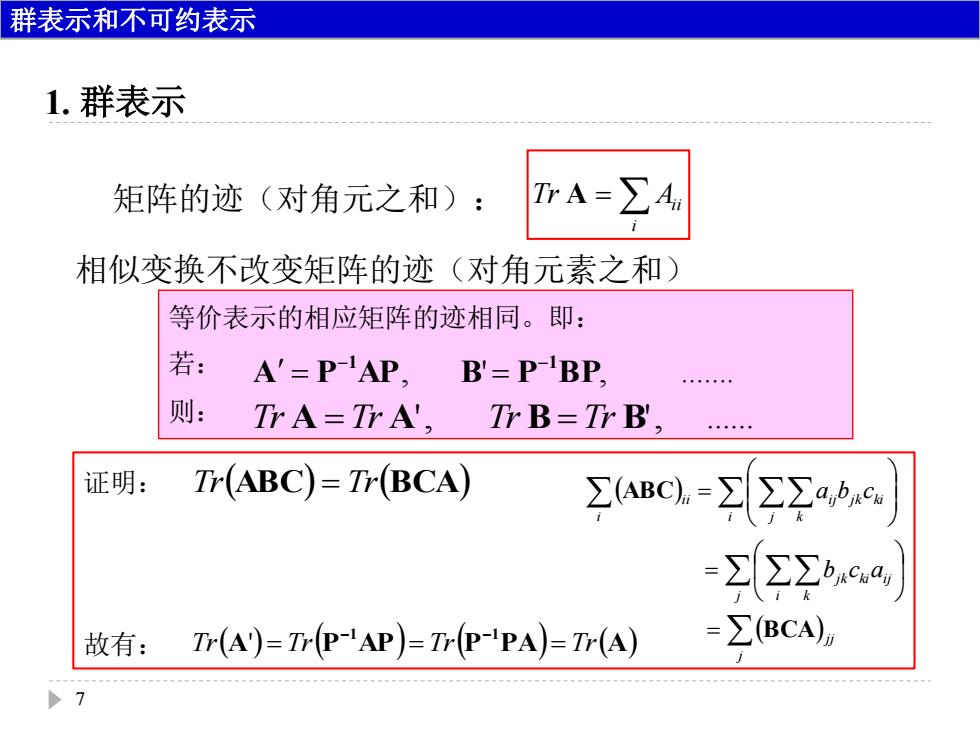
1. 群表示 7 i 矩阵的迹(对角元之和): Tr A Aii 相似变换不改变矩阵的迹(对角元素之和) 等价表示的相应矩阵的迹相同。即: 若: 则: Tr A Tr A' , Tr B Tr B' , . A P AP, B' P B P, . 1 1 TrABC TrBCA j jj j i k jk ki ij i j k ij jk ki i ii b c a a b c BCA 证明: ABC 故有: A P AP P P A A 1 1 Tr Tr Tr Tr ' 群表示和不可约表示

群表示和不可约表示 1.群表示 3)、特征标 群表示理论中,矩阵的迹称特征标: x(R)=TrR 两个表示等价的充要条件是特征标相同。 {z(R={z.(=} 群的一个多维表示一定有无穷多个表示与之等价,且这些 表示相互等价
1. 群表示 8 3)、特征标 群表示理论中,矩阵的迹称特征标: 两个表示等价的充要条件是特征标相同。 (R ˆ ) Tr R G (R ˆ ) R ˆ . G' (R ˆ ) R ˆ . 群的一个多维表示一定有无穷多个表示与之等价,且这些 表示相互等价。 群表示和不可约表示

群表示和不可约表示 1.群表示 定理:同一共轭类的群元素,其特征标相同。 [证]设: A,B,∈G 且A与B共轭: A=氵1B求 群元素: A,B,1 相应的矩阵: A,B,X,X- 则由群表示的定义:A=X-BX 矩阵与操作有 相同的乘积关系 且: XX-=E 所以: (=x(B) (相似变换不改变矩阵的迹)
1. 群表示 9 定理:同一共轭类的群元素,其特征标相同。 [证] 设: 所以: A ˆ , B ˆ , X ˆ G A ˆ X ˆ B ˆ X ˆ 1 A X BX 1 ) ˆ ) ( ˆ (A B (相似变换不改变矩阵的迹 ) 相应的矩阵 : 1 A, B, X, X XX E 1 且 A 与 B共轭: 则由群表示的定义: 且: 1 ˆ , ˆ , ˆ , ˆ 群元素: A B X X 群表示和不可约表示 矩阵与操作有 相同的乘积关系

群表示和不可约表示 2.可约与不可约表示 1)、矩阵的直和 1 V3 I 0 例: 3 3 2 2 0 可分解为两个子方阵: C= 021-3 C$=) 2 矩阵的直和:C3=C?⊕C >10
2. 可约与不可约表示 10 例: 矩阵的直和 : 0 0 1 0 2 1 2 3 0 2 3 2 1 C3 2 1 2 3 2 3 2 1 a C3 1 b C3 b 3 a C3 C3 C 可分解为两个子方阵: 1)、矩阵的直和 群表示和不可约表示