
讨论: ■对于复杂的连续反应,通常需解联立 的微分方程,比较复杂。 ■所以在动力学研究中常采用一些近似 方法:如稳态近似法等
对于复杂的连续反应,通常需解联立 的微分方程,比较复杂。 所以在动力学研究中常采用一些近似 方法:如稳态近似法等。 讨论:

稳态近似法 1.假设中间产物的浓度不随时间变化 d[B] =0 dt B]=kL4]-k[B]=0 dt [8=[A k2
稳态近似法 [ ] 0 d B dt 1 2 [ ] [ ] k B A k 1 2 [ ] [ ] [ ] 0 d B k A k B dt 1. 假设中间产物的浓度不随时间变化

2.解简化方程求最终产物C~t关系 dIC]=k[B=k[=[4] dt K dIC]=k[4]-=kLAbe M dt [C]=[A]o(1-et)
1 2 2 1 2 [ ] [ ] [ ] [ ] d C k k B k A k A dt k 2. 解简化方程求最终产物C~t关系 1 1 1 0 [ ] [ ]= [ ] d C k t k A k A e dt 1 1 1 0 [ ] [ ]= [ ] d C k t k A k A e dt 1 0 [ ] [ ] (1 ) k t C A e

对 比 精确推导 稳态近似 [C]=[A](1- e+ k k2-k k2 -k [A]=[4loe-kv [B]= kiAb (er-e) k2-k 1-会 [4]=[4lek [C]=[A](1-e4)
对 比 精确推导 稳态近似 1 0 [ ] [ ] (1 ) k t C A e 1 2 [ ] [ ] k B A k 1 0 [ ] [ ] k t A A e 1 0 [ ] [ ] k t A A e 1 0 1 2 2 1 [ ] [ ] ( ) k A k t k t B e e k k 2 1 1 2 0 2 1 2 1 [C] [ ] (1 ) k k k t k t A e e k k k k

10 96 k/k2=0.05 4 Ass 2 0.05M K[A] time.s
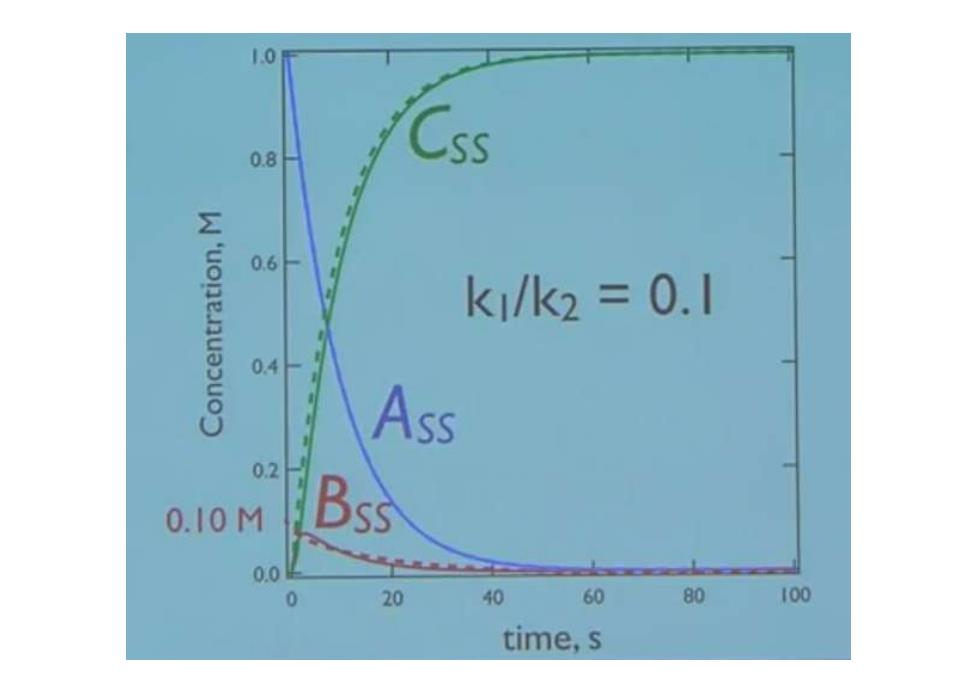
1.0 0.8 Css 0.6 k1/k2=0.1 04 Ass 02 0.10M Bss 0.0 0 20 40 60 80 100 time,s
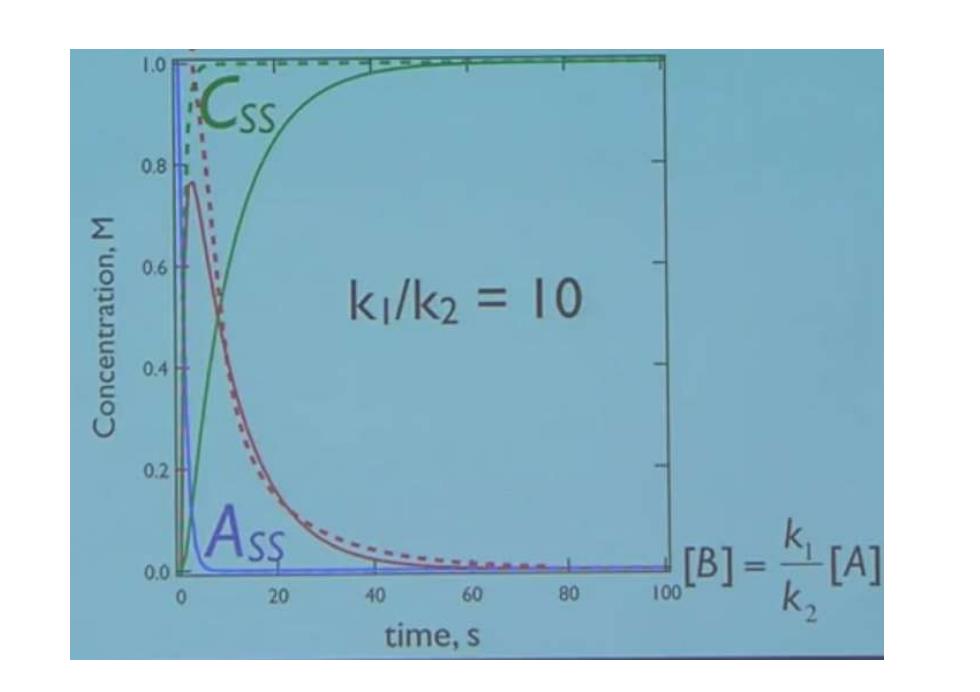
10 08 0.6 k/k2=10 04 02 0.0 Ass [AT 0 40 60 80 [B]-K2 100 time,s

§11.7速率常数与温度的关系 ·在平行反应中,我们可以调节温度来改变产 物比,是基于k/k'随温度T的改变。 ·那么,速率常数与温度的定量关系究竟如何 呢? 一、k~T关系的几种类型: ·温度对k的影响比较复杂,大致可分以下 几类情况:
§11.7 速率常数与温度的关系 • 在平行反应中,我们可以调节温度来改变产 物比,是基于k / k 随温度T 的改变。 • 那么,速率常数与温度的定量关系究竟如何 呢? 一、k T 关系的几种类型: • 温度对 k 的影响比较复杂,大致可分以下 几类情况:
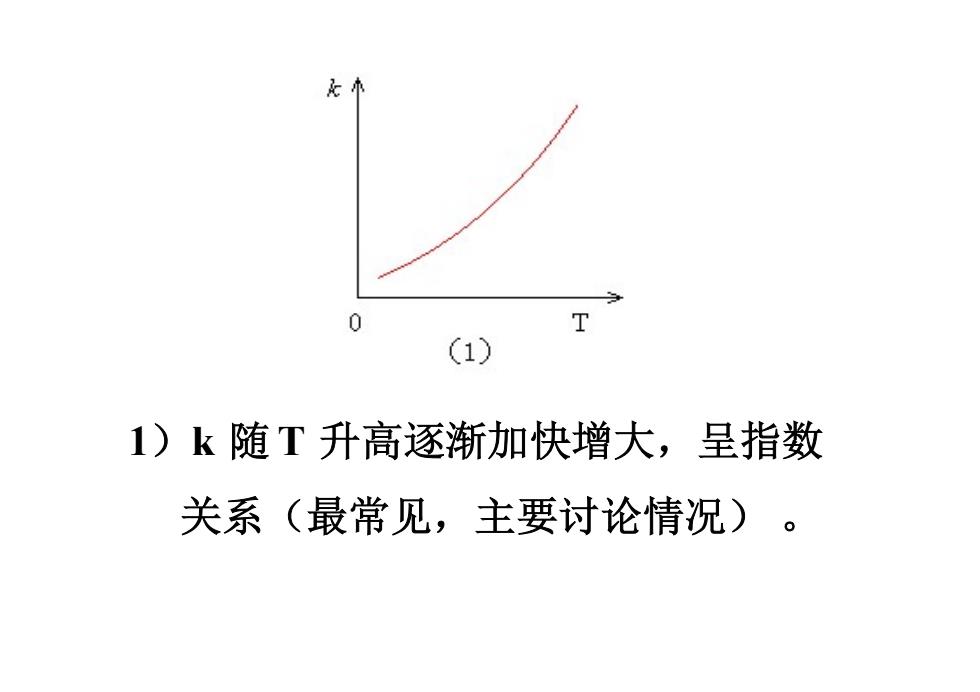
(1) 1)k随T升高逐渐加快增大,呈指数 关系(最常见,主要讨论情况)
1)k 随 T 升高逐渐加快增大,呈指数 关系(最常见,主要讨论情况)
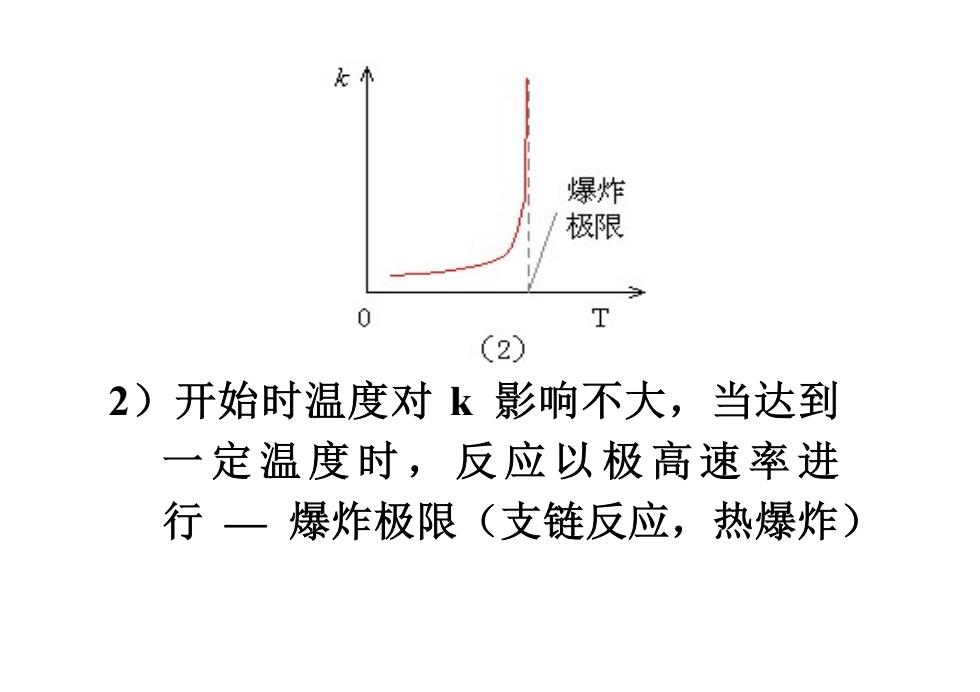
爆炸 /极限 0 T (2) 2)开始时温度对k影响不大,当达到 一定温度时,反应以极高速率进 行一爆炸极限(支链反应,热爆炸)
2)开始时温度对 k 影响不大,当达到 一 定温 度 时, 反 应以 极 高速 率 进 行 — 爆炸极限(支链反应,热爆炸)