
第一讲:回顾 从量子力学产生到双原子分子体系电子结构 X.J.WU @USTC
第一讲:回顾 从量子力学产生到双原子分子体系电子结构 1 X. J. WU @ USTC

量子力学基础 小结 量子论的实验基础、德布罗意-爱因斯坦关系、测不准关系 波函数(波函数的统计解释、标准条件、自由电子的波函数) 算符(乘法和对易、本征方程、常见的力学量算符(坐标、动量、角 动量、能量等)) 线性算符、厄密算符的定义和性质 Schrodinger?方程(定态、含时) 势箱中粒子的定态解(能量、波函数) 波函数按力学量本征函数系展开,力学量的可测值和几率、平均值 对易力学量(共同本征函数系、测不准关系) 轨道角动量(定义、对易关系、本征方程及其解) 2 X.J.WU@USTC
量子力学基础 —— 小结 量子论的实验基础、德布罗意-爱因斯坦关系、测不准关系 波函数(波函数的统计解释、标准条件、自由电子的波函数) 算符(乘法和对易、本征方程、常见的力学量算符(坐标、动量、角 动量、能量等)) 线性算符、厄密算符的定义和性质 Schrodinger方程(定态、含时) 势箱中粒子的定态解 (能量、波函数) 波函数按力学量本征函数系展开,力学量的可测值和几率、平均值 对易力学量(共同本征函数系、测不准关系) 轨道角动量(定义、对易关系、本征方程及其解) 2 X. J. WU @ USTC

单原子体系 一一小结 氢原子和类氢离子的能级和波函数、量子数的物理意义、 波函数的图形表示 B-O近似、单电子近似、中心力场近似的基本思想 变分原理、简单多电子原子的变分法处理 电子自旋(自旋量子数、自旋磁矩)、全同性原理 多电子波函数的构成、行列式波函数 3 X.J.WU @USTC
单原子体系 —— 小结 氢原子和类氢离子的能级和波函数、量子数的物理意义、 波函数的图形表示 B-O近似、单电子近似、中心力场近似的基本思想 变分原理、简单多电子原子的变分法处理 电子自旋(自旋量子数、自旋磁矩)、全同性原理 多电子波函数的构成、行列式波函数 3 X. J. WU @ USTC

双原子体系 小结 线性变分法的基本思想、简单体系的线性变分处理 分子轨道理论(MO)的四个基本近似、成键三原则 简单同核、异核双原子分子的电子组态、键级(解离能、 键长) 电子光谱项 X.J.WU USTC
双原子体系 —— 小结 线性变分法的基本思想、简单体系的线性变分处理 分子轨道理论(MO)的四个基本近似、成键三原则 简单同核、异核双原子分子的电子组态、键级(解离能、 键长) 电子光谱项 4 X. J. WU @ USTC
量子力学的产生 頻率/s 10.1071010910010H10210310410510w10710w10910 可見光 波的名桐 無線電 紅外幅射 紫外辐射 加瑪射線 微波 X射線 NUN 波/m103102101101021031010-10101010910010102 楼宇 人類網球 蟻 细胞细菌病毒DNA 水份子 原子核短 大約尺寸 物质是否无限可分? 经典力学理论是否适用于微观粒子 X.J.WU@USTC
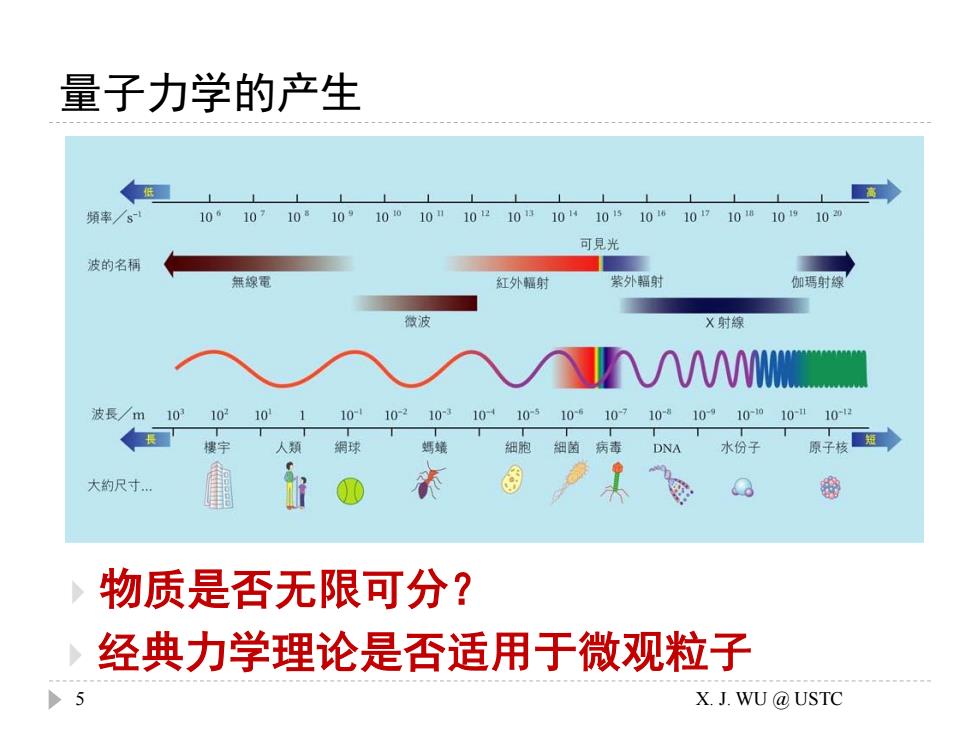
量子力学的产生 物质是否无限可分? 经典力学理论是否适用于微观粒子 5 X. J. WU @ USTC
从经典力学到量子力学 经典理论 Newton's Law Maxwell's Eq. 黑体辐射 旧量子论 新量子论 光电效应 能量量子 康普顿散射 微观粒子量子化 光的量子化 氢原子光谱 波尔理论 波的粒子性 粒子的波动性 物质波 s=hv 电子散射 波粒二象性 p=h/A 不确定原理 量子力学 6 X.J.WU@USTC
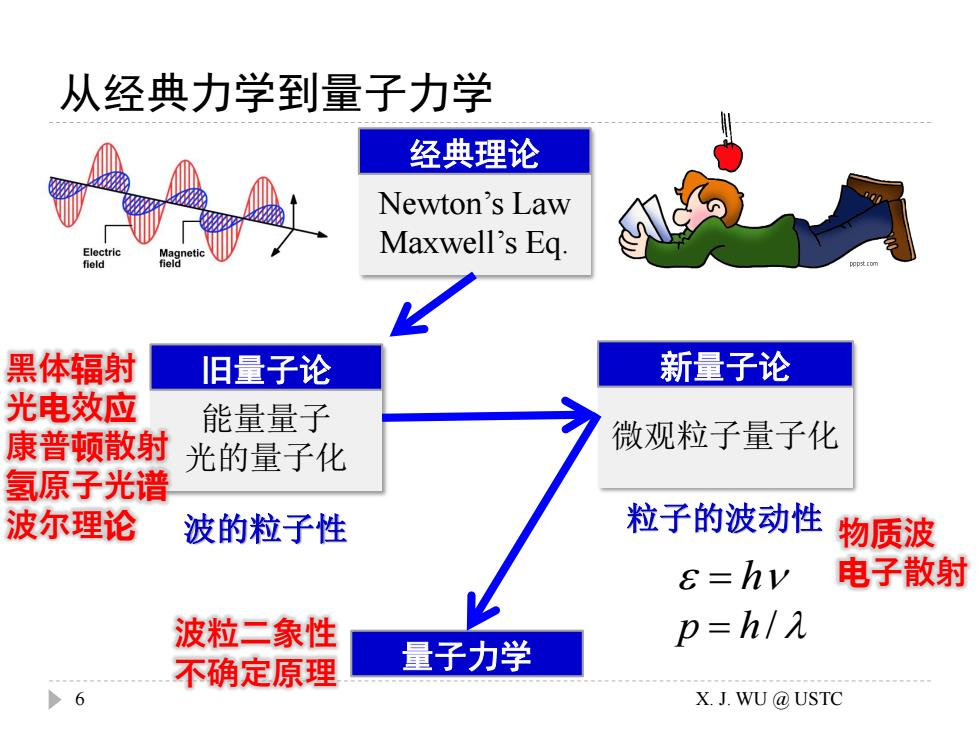
从经典力学到量子力学 Newton’s Law Maxwell’s Eq. 经典理论 能量量子 光的量子化 旧量子论 微观粒子量子化 新量子论 波的粒子性 粒子的波动性 量子力学 黑体辐射 光电效应 康普顿散射 氢原子光谱 波尔理论 物质波 = h 电子散射 波粒二象性 p = h / 不确定原理 6 X. J. WU @ USTC

物质波的统计规律-M.Born1926 对应于空间的一个状态,就有一个 伴随这状态的德布罗依波的几率。 若与电子对应的波函数在空间某点 为零,这就意味着在这点发现电子 的几率小到零。 波恩 量子力学: 波动性 可叠加性,不需要物理量在空间的分布 电子的波动性控制电子在不同区域出现的几率! X.J.WU USTC
物质波的统计规律 - M. Born 1926 对应于空间的一个状态,就有一个 伴随这状态的德布罗依波的几率。 若与电子对应的波函数在空间某点 为零,这就意味着在这点发现电子 的几率小到零。 ——波恩 量子力学: 波动性 可叠加性,不需要物理量在空间的分布 电子的波动性 控制 电子在不同区域出现的几率! 7 X. J. WU @ USTC

旧量子论:波尔原子结构模型(1913年) Bohr's Theory:Quantization Energy of H Atom(1913) Assumption:There are certain allowed orbits for which electron has a fixed energy.The electron loses energy only when it jumps between the allowed orbits and the atoms emits this energy as light of a given wave length. 。定态规则:电子运动于一组稳定的圆周轨道 (定态),原子在定态中不发射也不吸 n=3 收电磁辐射能。其角动量满足如下的量子化 n=2 条件:L=nlh/(2m)=nh n=1 ◆ △E=hv ●频率条件:电子从一个定态轨道跃 +Ze 迁到另外一个轨道时,会以电磁波的形 式放出(或吸收)能量v=|Em-En| 8 X.J.WU@USTC
—— Bohr’s Theory: Quantization Energy of H Atom (1913) ⚫ 定态规则:电子运动于一组稳定的圆周轨道 (定态),原子在定态中不发射也不吸 收电磁辐射能。其角动量满足如下的量子化 条件: L = nh/ (2π) = nћ ⚫ 频率条件:电子从一个定态轨道跃 迁到另外一个轨道时,会以电磁波的形 式放出(或吸收)能量 hv = | Em – En | Assumption: There are certain allowed orbits for which electron has a fixed energy. The electron loses energy only when it jumps between the allowed orbits and the atoms emits this energy as light of a given wave length. 旧量子论:波尔原子结构模型(1913年) 8 X. J. WU @ USTC
波粒二象性 束缚态电子:定态→驻波 de BroglieSchrodinger: 微观粒子的定态与驻波对应 入=2l/%,n=1,2,3. 氢原子的圆形电子轨道的驻波条件: 轨道周长=波长整数倍 )h/p 2元a=n入=nh/p wavelength 角动量 radius L=ap=nh/(2m)=nh X.J.WU@USTC
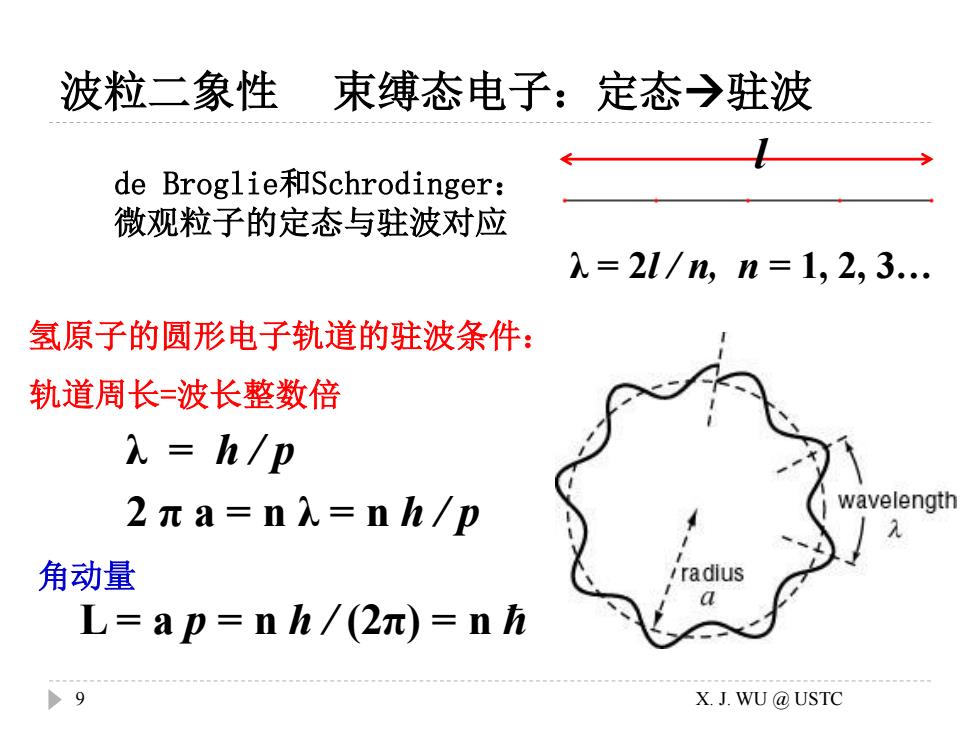
de Broglie和Schrodinger: 微观粒子的定态与驻波对应 氢原子的圆形电子轨道的驻波条件: 轨道周长=波长整数倍 λ = h / p 2 π a = n λ = n h / p L = a p = n h / (2π) = n ћ 角动量 λ = 2l / n, n = 1, 2, 3. l 波粒二象性 束缚态电子:定态→驻波 9 X. J. WU @ USTC

A.Piccard,E.Henriot,P.Ehrenfest,Ed.Herzen,Th.De Donder, E.Schroinger,E.Verschaffelt,W.Pauli,W.Heisenberg, R.H.Fowler,L.Brillouin 1932 9335 P.Debye,M.Knudsen,W.L.Bragg,H.A.Kramers,P.A.M.Dirac, A.H.Compton,L.de Broglie,M.Born,N.Bohr, 1929 1954192 1918 924 Langmuir,M.Planck,M.Curie,H.A.Lorentz,A.Einstein, P.Langevin,Ch.E.Guye,C.T.R.Wilson,O.W.Richardson 、,10 X.J.WU @USTC Photograph by Benjamin Couprie,Institut International de Physique Solvay,Brussels,Belgium
1918 1921 1929 1922 1932 1933 1933 1954 10 X. J. WU @ USTC