
第2章线性时不变系统的 时域分析
第 2章 线性时不变系统的 时域分析

主要内容 连续时间系统的时域分析:卷积积分 离散时间系统的时域分析:卷积和 冬LTI系统的性质 第2章线性时不变系统 2
第2章 线性时不变系统 2 主要内容 连续时间系统的时域分析:卷积积分 离散时间系统的时域分析:卷积和 LTI系统的性质

学习目标 ·掌握卷积积分与卷积和两种计算; 了解常系数微分方程和差分方程的经典算法; 理解LTI系统的冲激响应h(); 冬理解系统的零输入响应、零状态响应。 第2章线性时不变系统 3
第2章 线性时不变系统 3 学习目标 掌握卷积积分与卷积和两种计算; 了解常系数微分方程和差分方程的经典算法; 理解LTI系统的冲激响应h(t); 理解系统的零输入响应、零状态响应

2.0引言 LTI系统(线性时不变系统)的输入用一组基本信 号的线性组合来表示,就可以根据该系统对这些基 本信号的响应,再利用1.6.6节我们所介绍过的叠加 性质来求得整个系统的输出。 。新概念—卷积和/卷积积分
2.0 引言 LTI系统(线性时不变系统)的输入用一组基本信 号的线性组合来表示,就可以根据该系统对这些基 本信号的响应,再利用1.6.6节我们所介绍过的叠加 性质来求得整个系统的输出。 新概念——卷积和/卷积积分

2.1离散时间LTI系统一卷积和 δn] n 单位脉冲的采样性质 x[n]o[n]=x[0]δ[n] xIn]oln-no]=x[nololn-nol x[n]=∑x[k][n-k] k=-∞ 任意一个序列都可以表示成一串移位的单位脉冲序列6/-k的线性组合 第2章线性时不变系统 5
第2章 线性时不变系统 5 2.1离散时间LTI系统—卷积和 单位脉冲的采样性质 δ = δ nxnnx ][]0[][][ ][][][][ δ 0 0 δ −=− nnnxnnnx 0 +∞ = −∞ = − k δ knkxnx ][][][ 任意一个序列都可以表示成一串移位的单位脉冲序列δ[n-k]的线性组合
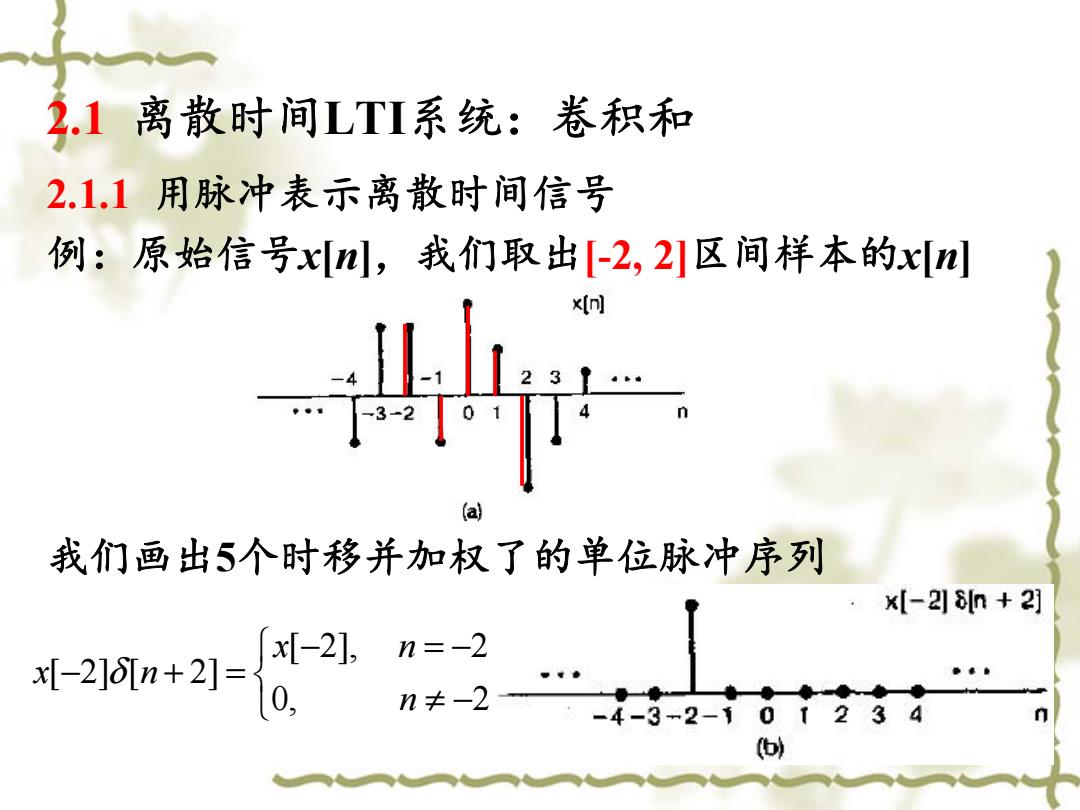
2.1离散时间LTI系统:卷积和 2.1.1用脉冲表示离散时间信号 例:原始信号x[m,我们取出[-2,2区间样本的x[m n a 我们画出5个时移并加权了的单位脉冲序列 .x[-2]8n+2] [-2], x1-20n+21=0 n=-2 n≠-2 -4-3-2-101234 (b)
2.1 离散时间LTI系统:卷积和 2.1.1 用脉冲表示离散时间信号 例:原始信号x[n],我们取出[-2, 2]区间样本的x[n] 我们画出5个时移并加权了的单位脉冲序列 [ 2], 2 [ 2] [ 2] 0, 2 x n x n n δ − =− − += ≠ −
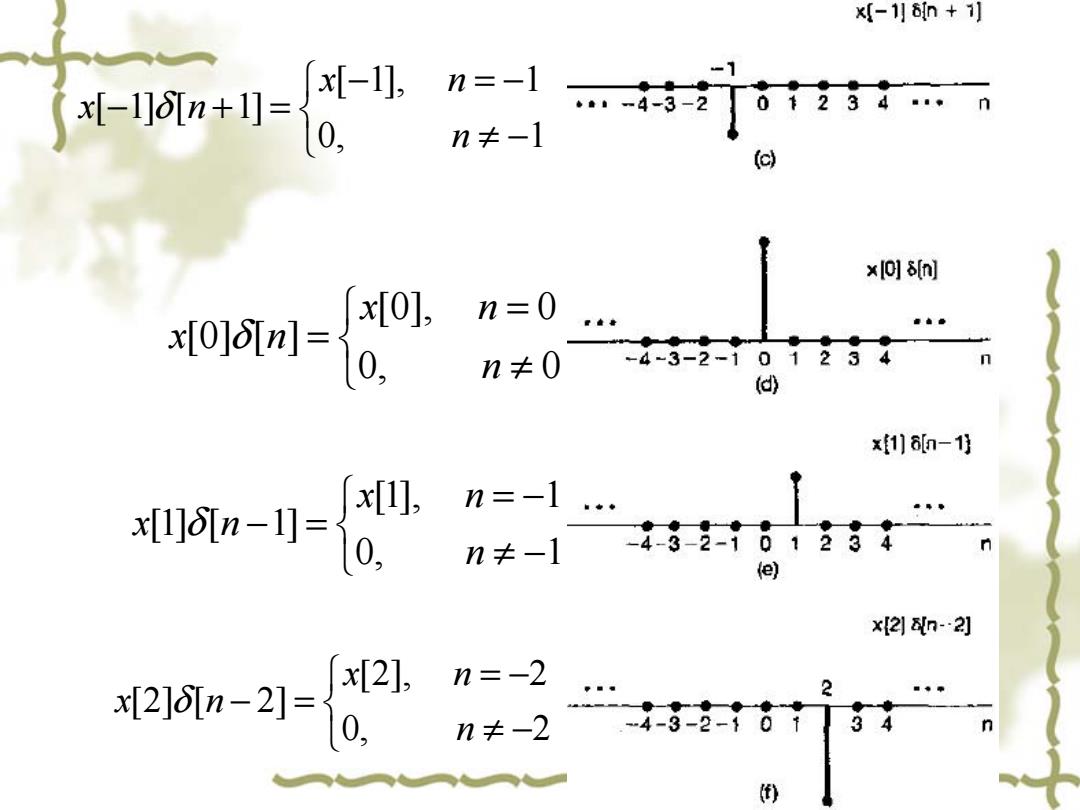
x(-1月n+] x[-1], x[-1]6[n+1]= 0, (c) x[0]8(n] x[0], n=0 0m={ 0, n≠0 -4-3-2-101234 (d) xf116n-10 xn-= x[1], n=-1… n≠- 1401 (e) x2n-2 2n-207 2 n≠-2 3 )
[ 1], 1 [ 1] [ 1] 0, 1 x n x n n δ − =− − += ≠ − [0], 0 [0] [ ] 0, 0 x n x n n δ = = ≠ [1], 1 [1] [ 1] 0, 1 x n x n n δ = − − = ≠ − [2], 2 [2] [ 2] 0, 2 x n x n n δ = − − = ≠ −

图中这5个序列的和就等于在-2≤n≤2区间的x[n。 若扩大到包含更多的移位加权脉冲,从而 x[n]=.+x[-3]n+3]+x[-2]n+2] +x[-1]n+1]+x[0]Ln] +x[1][n-1]+x[2]n-2] +x[3]6n-3]+. 十0∞ 即x[n=∑x[k]n-k] n]=∑Ln-k] k=-o∞ k=0 这样,就把任意一个序列表示成一串移位的单位脉 冲序列6[-的线性组合,而这个线性组合式中的 加权因子就是x。称为离散时间单位脉冲序列的 筛选性质
图中这5个序列的和就等于在-2≤n ≤2区间的x[n]。 若扩大到包含更多的移位加权脉冲,从而 即 这样,就把任意一个序列表示成一串移位的单位脉 冲序列δ [n-k]的线性组合,而这个线性组合式中的 加权因子就是x [k]。称为离散时间单位脉冲序列的 筛选性质。 [ ] ... [ 3] [ 3] [ 2] [ 2] [ 1] [ 1] [0] [ ] [1] [ 1] [2] [ 2] [3] [ 3] ... xn x n x n x n xn xn x n x n δ δ δ δ δ δ δ =+− ++− + +− ++ + −+ − + −+ [] [][ ] k x n xk n k δ +∞ =−∞ = − 0 [] [ ] k un n k δ +∞ = = −
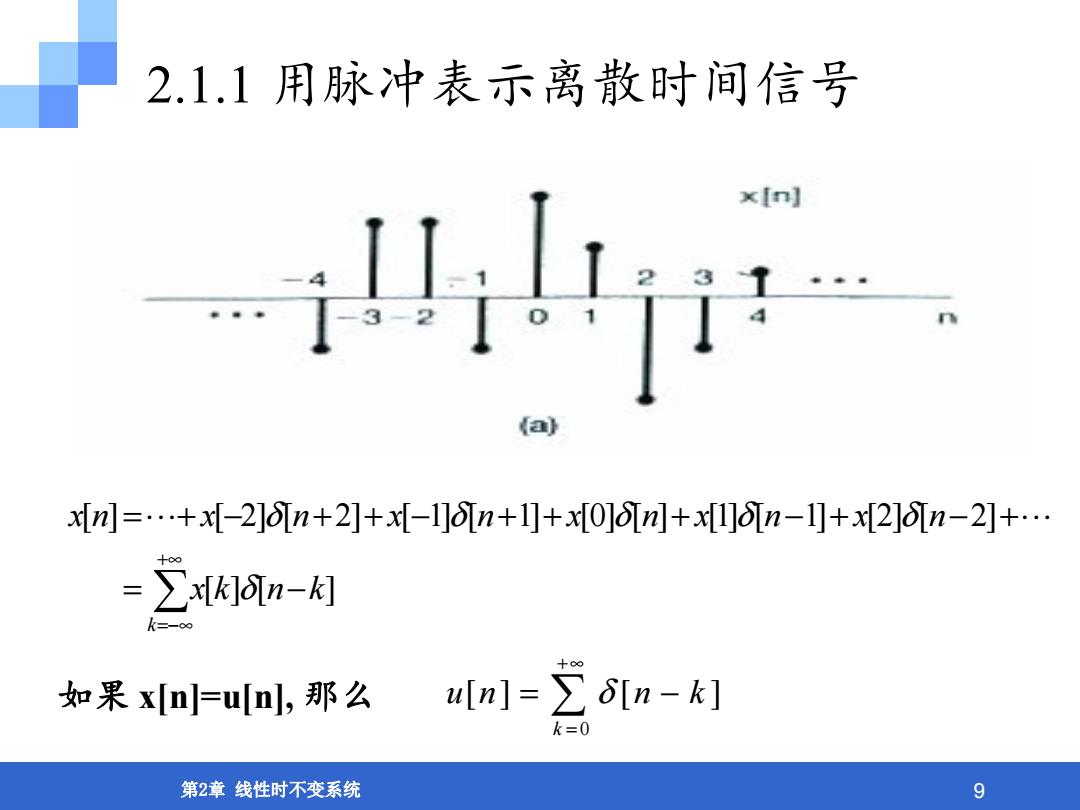
2.1.1用脉冲表示离散时间信号 x[n] 3 32 a x[m川=+x[-2]n+2]+x[-1]n+1+x[0]n+x[]n-l]+x[2]n-2]+… =∑x[]n- k=-o∞ 如果xn=un,那么 u[n]=∑6[n-k] k=0 第2章线性时不变系统 9
第2章 线性时不变系统 9 2.1.1 用脉冲表示离散时间信号 ∞+ =−∞ = − +−+−+++−++−+= k knkx nxnxnxnxnxnx ][][ ]2[]2[]1[]1[][]0[]1[]1[]2[]2[][ δ δ δ δ δ δ 如果 x[n]=u[n], 那么 0 [] [ ] k un n k δ +∞ = = −

2.1.2离散时间LTI系统的单位脉冲响应及卷积和表示 一个线性系统对x[的响应就是系统对这些移位脉冲 的每一个响应加权后的叠加;再者,时不变性又意 味这一个时不变系统对移位单位脉冲的响应就是未 被移位情况下单位脉冲响应的移位。 考虑某一线性(可能是时变的)系统对任一输入[ 的响应。由于可以将输入表示为一组移位单位脉冲 的线性组合,令hm记为该线性系统对移位单位脉 冲5[-k的响应,那么根据叠加性质,该线性系统 对输入x的响应y就是这些基本响应的加权线性 组合,即: yn=∑x[kh[nl 式2.3 k=-o∞
2.1.2 离散时间LTI系统的单位脉冲响应及卷积和表示 一个线性系统对x [ n ]的响应就是系统对这些移位脉冲 的每一个响应加权后的叠加;再者,时不变性又意 味这一个时不变系统对移位单位脉冲的响应就是未 被移位情况下单位脉冲响应的移位。 考虑某一线性(可能是时变的)系统对任一输入x [ n] 的响应。由于可以将输入表示为一组移位单位脉冲 的线性组合,令 h k [ n ]记为该线性系统对移位单位脉 冲 δ [ n - k ]的响应,那么根据叠加性质,该线性系统 对输入x [ n ]的响应y [ n ]就是这些基本响应的加权线性 组合,即: [] [] [] k k yn xkh n +∞ =−∞ = 式2.3