
第8章离散时间系统的Z域分析 8.1离散信号的z变换及收敛域 8.2z逆变换 8.3z变换的基本性质 8.4利用z变换解差分方程 8.5离散系统的系统函数 8.6序列的傅里叶变换 8.7离散时间系统的频率响应特性
第8章 离散时间系统的z域分析 8.1 离散信号的 z变换及收敛域 8.2 z逆变换 8.3 z变换的基本性质 8.4 利用 z变换解差分方程 8.5 离散系统的系统函数 8.6 序列的傅里叶变换 8.7离散时间系统的频率响应特性

本章主要内容 (1)Z变换、性质及其收敛域 (2)利用z变换求解差分方程 (3)离散系统的系统函数 (4)系统稳定性及因果性
(1) Z变换、性质及其收敛域 (2) 利用z变换求解差分方程 (3) 离散系统的系统函数 (4) 系统稳定性及因果性 本章主要内容

8.1离散信号的z变换及收敛域 8.1.1z变换定义 z变换的定义可以由取样信号的拉氏变换引出, 也可以直接对离散信号给予定义。 x[n的双边z变换:X(a)=∑n” 17=-0 =+x灯-2]p2+[-12+x0]++x[2]z2+… x[刀]的单边z变换:X(a)=z(列=∑”=0]++22+… 对z变换式的理解xa)=xm2”=-2z+2 的正幂 +x0)z°+x①)z1+x2)z2+xz"+.. 1)X(z)是z1的幂级数2)级数的系数是x(n) 的负暴 3)幂-n中的n指出x(n)的位置
8.1 离散信号的z 变换及收敛域 z变换的定义可以由取样信号的拉氏变换引出, 也可以直接对离散信号给予定义。 8.1.1 z 变换定义 x[n]的双边z 变换: =L+ − + − + + + +L = − − − +∞ =−∞ ∑ 2 1 1 2 [ 2] [ 1] [0] [1] [2] ( ) [ ] x z x z x x z x z X z x n z n n x[n]的单边z 变换: ( ) 1 2 0 ( ) [ ] [ ] [0] [1] [2] n n X z xn xnz x x z x z ∞ − −− = =Z = =+ + + ∑ L ∑ ∞ =−∞ − = n n X(z) x(n)z 14 2 44444 4444443 L K 14 2 44 4 3 44 K 的负幂 的正幂 z n z x z x z x z x n z x z x z + + + + + = − + − − − − (0) (1) (2) ( ) ( 2) ( 1) 0 1 2 对 2 1 z变换式的理解 1)X (z)是 z −1的幂级数 3)幂− n中的n指出 x(n) 的位置 2)级数的系数是 x (n)
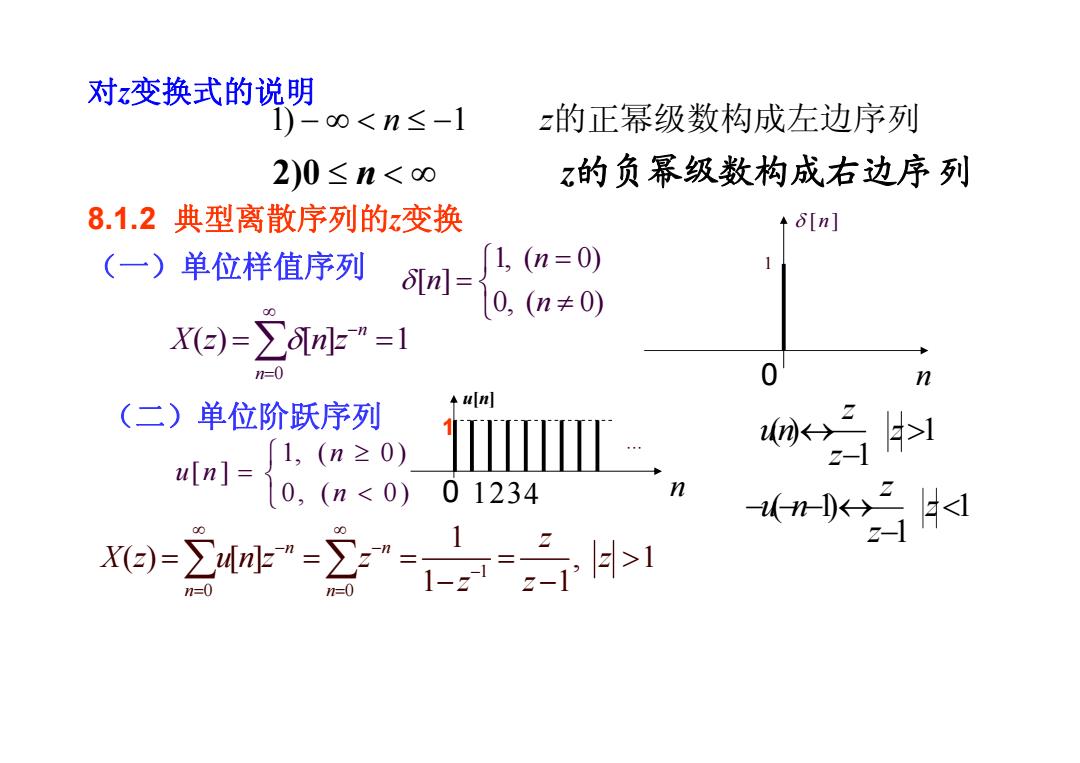
对z变换式的说明 1)-ol n等
对 z变换式的说明 2 ) 0 ≤ n − − ∑ ∑ 1 1 ( 1) − ↔ z z z u n
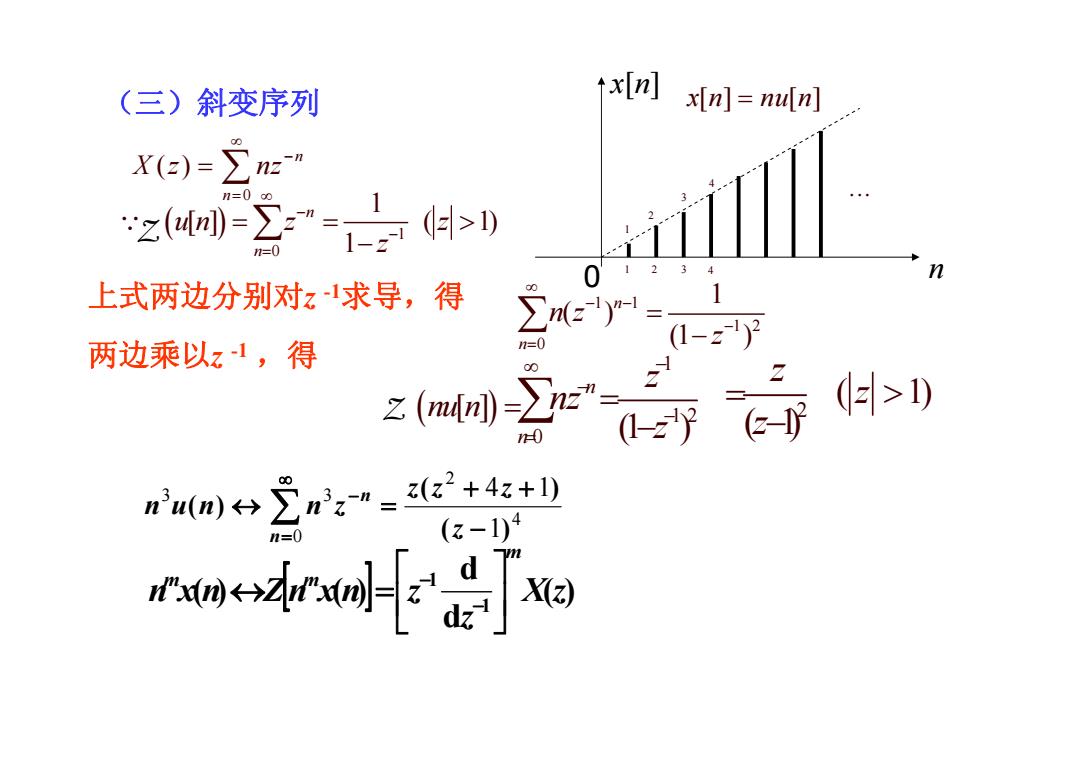
(三)斜变序列 txIn]xin]=nuln] X(e)-∑ne" z2) 7=0 1=0 0 12 n 上式两边分别对z求导,得 ∑ey=, (1-z)2 两边乘以z1,得 1=0 之(ma)∑e”- (2>1) 0 0-z 2- nu(m)9∑n2"=2(22+4z+ 0 (z-1)4 awor-x
0 ( ) n n X z nz ∞ − = = ∑ ( ) 1 0 1 [ ] ( 1) 1 n n un z z z ∞ − − = == > − QZ ∑ x [ n ] 0 n 1 1 2 2 3 3 4 4 L (三)斜变序列 x[] [] n nu n = 上式两边分别对z -1求导,得 1 1 1 2 0 1 ( ) (1 ) n n n z z ∞ − − − = = − ∑ 两边乘以z -1 ,得 1 1 2 0 (1 ) n n z nz z ∞ − − − = = − ∑ 2 ( 1) z z = − Z (nu n[ ] ) = ( 1) z > 4 2 0 3 3 1 4 1 ( ) ( ) ( ) − + + ↔ = − ∞ = ∑ z z z z n u n n z n n [ ] ( ) d d ( ) ( ) 1 1 X z z n x n Z n x n z m m m ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ↔ = − −

x,[n] (四)指数序列 (0 x2[n] (2)左边指数序列 3-2-1 0 n x2[n]=-a"u[-n-1] (a>1) d-d-w-M->co>--odd 结论:右边边序列收敛域为圆外的部分,左边序列收敛域为圆内部5 两个不同的序列对应于相同的z变换,但z变换收敛域不同。 双边序列收敛域是怎样的呢?
(2)左边指数序列 2 [ ] [ 1] n x n au n = − −− ( ) 0 [] , n nn n z aun a z z a z a ∞ − = == > − Z ∑ 0 1 1 2 3 4 k 1 x [ ] n (0 1) L ( ) 1 [ 1] ( ) , n nn n z au n a z z a z a − − =−∞ − −− = − = < − Z ∑ 结论:右边边序列收敛域为圆外的部分,左边序列收敛域为圆内部分 双边序列收敛域是怎样的呢? 两个不同的序列对应于相同的z变换,但z变换收敛域不同

例:已知序列为x[n=au[m-b[-n-1],求它的z变换,并确定 收敛域。 解.-立t立0乃t-立+元g 1-b22-b 日ld e)= la-a<8 1-a z-a =0 结论:双边序列收敛域为一个圆环。 例:x[n=2"[n-3"u[-n-1]的z变换,并确定收敛域。 24<3
例:已知序列为x [n]=anu[n] -bnu[-n-1],求它的z变换,并确定 收敛域。 解: n n X z xnz− ∞ =−∞ ( )=∑( ) n n n n x nz xnz − ∞ = − − =−∞ =∑ +∑ 0 1 ( ) ( ) n n n n n n b z a z− ∞ = − − =−∞ = ∑− +∑ 0 1 ( ) ∑ − =−∞ − − − 1 1 ( ) n n b z z b z b z b z − = − = − − 1 1 1 ∑ ∞ = − 0 1 ( ) n n az z a z az − = − = −1 1 1 z a a z b z a z z b z X z < < − + − ( )= 例:x [n]=2nu[n] -3nu[-n-1]的z变换,并确定收敛域。 2 3 3 2 ( ) < < − + − = z zz zz X z 结论:双边序列收敛域为一个圆环

结论: ★收敛域内不包含任何极点(以极点为边界); ★有限长序列的收敛域为整个z平面 (可能除去z=0和z=0); ★右边序列的ROC为Z=R的圆外;ROC:Z>a ★左边序列的ROC为} =R的圆内;ROC:z<a ★双边序列的ROC为R<E<R2的圆环
结论: ★ 收敛域内不包含任何极点(以极点为边界); ★有限长序列的收敛域为整个 z 平面 (可能除去z = 0 和z = ∞); ★右边序列的ROC为 的圆外; R1 z = ★左边序列的ROC为 的圆内; R2 z = ★双边序列的ROC为 的圆环。 1 R2 R a ROC: z < a

(五)单边正、余弦序列 x[n] 1 0 12 n 令指数序列中d=ea",那么a=em,>e=l =a,-s11h一@44例支ae列 Z(z-C0s风) 2-2zc0s4+1 同理: zsin @o (sin @on)uin]2=cos@o+I 1z>1
(五)单边正、余弦序列 x[n] 0 1 1 2 n 0 n j n a e ω = 0 j a e ω = 0 1 j z e ω 令指数序列中 ,那么 , > = 0 0 2 0 sin (sin ) [ ] 2 cos 1 z nun z z ω ω ω ↔ − + 同理: z > 1

8.1.3z变换的收敛域 收敛域:对序列x),能满足级数绝对可和所有z的范 围。 ∑x[n0
8.1.3 z变换的收敛域 收敛域:对序列x(n),能满足级数绝对可和所有z的范 围。 [ ] n n xnz ∞ − =−∞ ∑ 0 n