
第7章 离散时间系统的时域分析 7.1离散时间信号 7.2离散时间系统的数学模型 7.3常系数线性差分方程的求解 7.4零输入响应与零状态响应 7.5卷积
第7章 离散时间系统的时域分析 7.3 常系数线性差分方程的求解 7.1 离散时间信号 7.2 离散时间系统的数学模型 7.4 零输入响应与零状态响应 7.5 卷积

离散时间系统:激励与响应都是离散时间信号的系统。 离散时间系统的优点 精度高 可靠性好 功能灵活 时分复用 保密性好 便于大规模集成
离散时间系统的优点 精度高 可靠性好 功能灵活 时分复用 保密性好 便于大规模集成 离散时间系统:激励与响应都是离散时间信号的系统
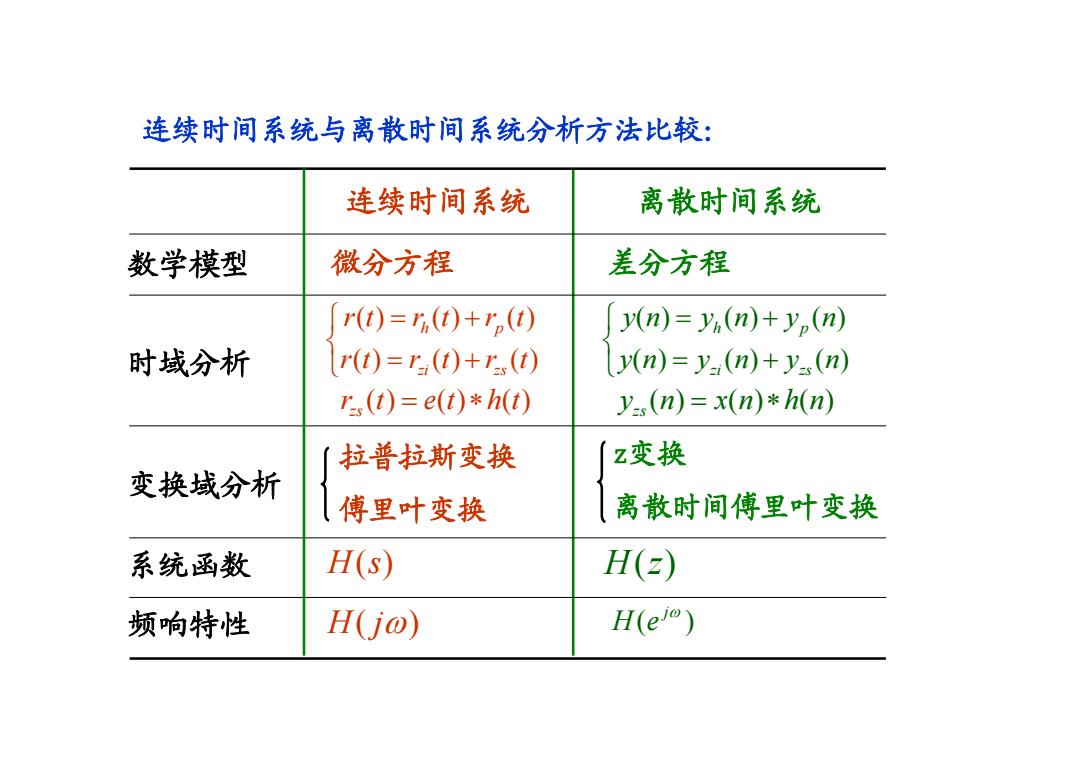
连续时间系统与离散时间系统分析方法比较: 连续时间系统 离散时间系统 数学模型 微分方程 差分方程 r(t)=r(t)+r(t) y(n)=yi(n)+y(n) 时域分析 r(t)=r(t)+r(t) y(n)=y:(n)+y(n) r(t)=e(t)*h(t) y.(n)=x(n)*h(n) 拉普拉斯变换 z变换 变换域分析 傅里叶变换 离散时间傅里叶变换 系统函数 H(s) H( 频响特性 H(jo) H(e)
连续时间系统与离散时间系统分析方法比较: 数学模型 微分方程 差分方程 系统函数 时域分析 变换域分析 频响特性 拉普拉斯变换 傅里叶变换 z变换 离散时间傅里叶变换 H ( s ) H ( j ω) H ( z ) ( ) j ω H e 连续时间系统 离散时间系统 () () () () () () h p zi zs rt r t r t rt r t r t ⎧ = + ⎨ ⎩ = + () () () zs r t et ht = ∗ () () () () () () h p zi zs y n y n y n y n y n y n ⎧ = + ⎨ ⎩ = + () () () zs y n xn hn = ∗
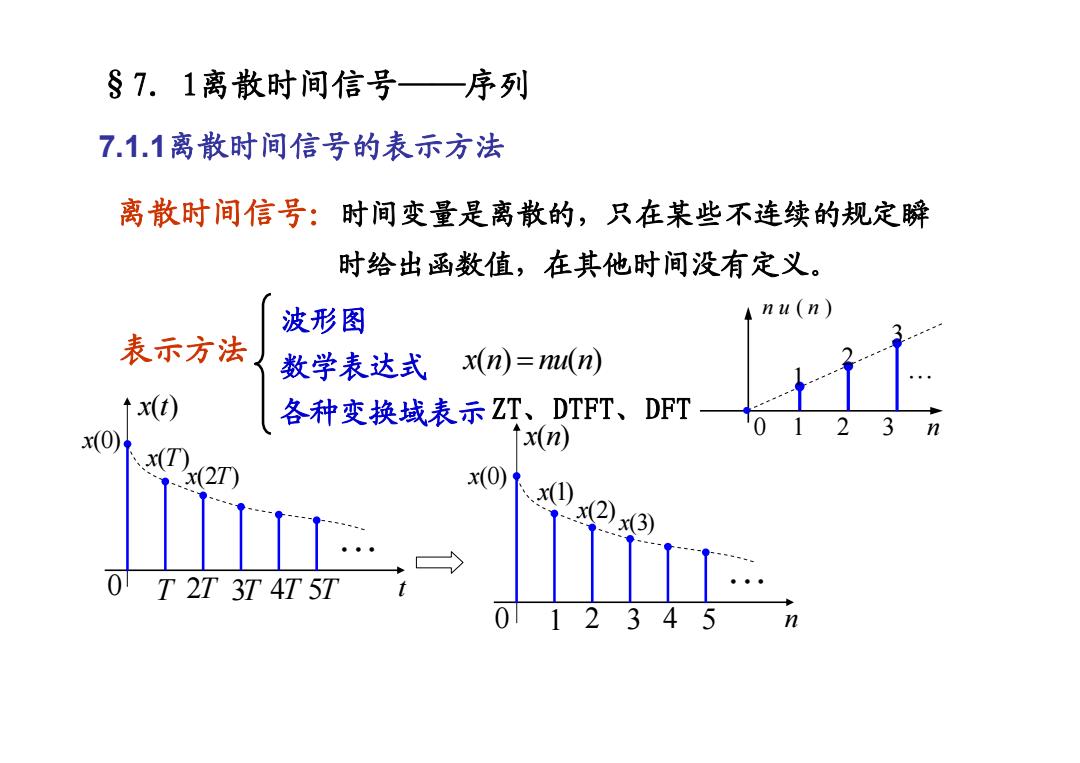
§7.1离散时间信号一序列 7.1.1离散时间信号的表示方法 离散时间信号:时间变量是离散的,只在某些不连续的规定瞬 时给出函数值,在其他时间没有定义。 波形图 A nu(n) 表示方法 数学表达式x(n)=mu(n) ↑x(t) 各种变换域表示ZT、DTFT、DFT一 x(n) x(2T) x(0)1 x(3) 0 T 2T 3T 4T 5T 012345
§7. 1离散时间信号——序列 7.1.1离散时间信号的表示方法 离散时间信号:时间变量是离散的,只在某些不连续的规定瞬 时给出函数值,在其他时间没有定义。 x( )t x(0) x(T) x(2T) T 2T 3T 4T 5T t L 0 x( ) n x(0) x(1) x(2) x(3) 1 2 3 4 5 n L 0 波形图 数学表达式 各种变换域表示 表示方法 x() () n nu n = ZT、DTFT、DFT 0 1 2 3 n nu n( ) • 1 2 3
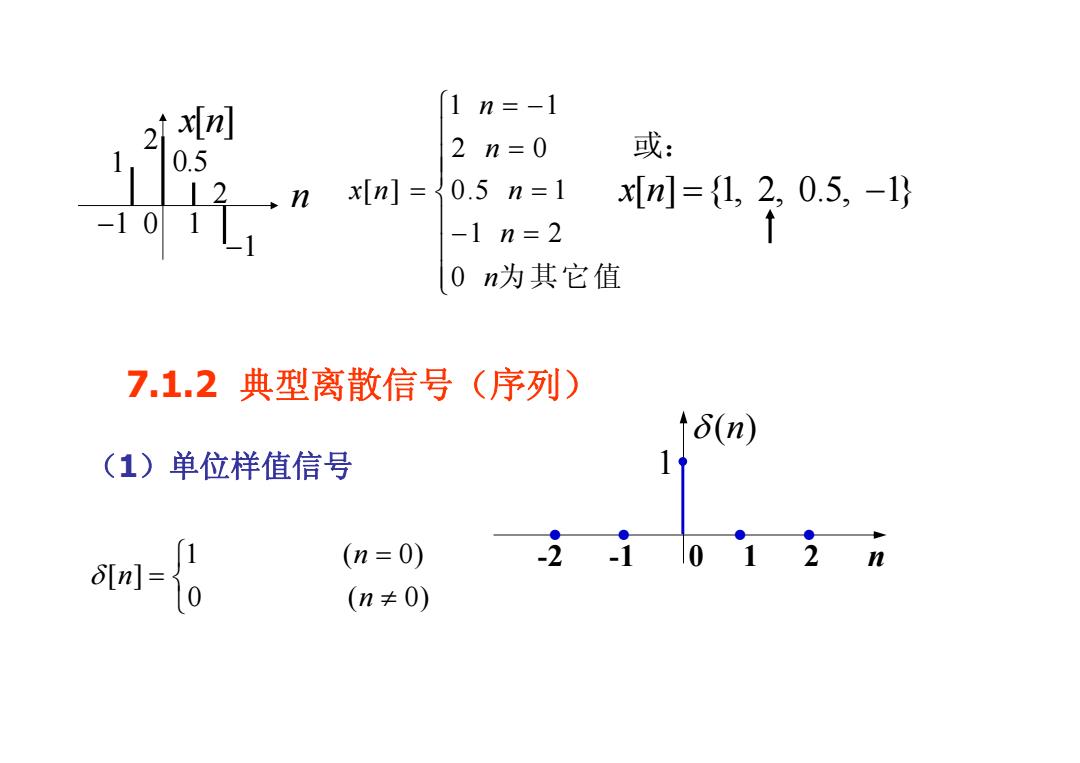
xn 1n=-1 2 0.5 2n=0 或: ↓2nxm=0.5n=1 x[n]={1,2,0.5,-l -101 -1 n=2 0n为其它值 7.1.2典型离散信号(序列) t6(n) (1)单位样值信号 otl- (n=0) 2i01 2 1 (n≠0)
1 1 2 0 [ ] 0.5 1 1 2 0 n n xn n n n ⎧ = − ⎪ = ⎪⎪ = = ⎨⎪− = ⎪⎪⎩ 为其它值x n[ ] {1, 2, 0.5, 1} = − 或: −1 0 1 2 n x[ ] n 2 1 −1 0.5 (1)单位样值信号 1 ( 0) [ ] 0 ( 0) n n n δ ⎧ = = ⎨⎩ ≠ 7.1.2 典型离散信号(序列) -2 -1 0 1 2 n • • • • δ ( ) n 1
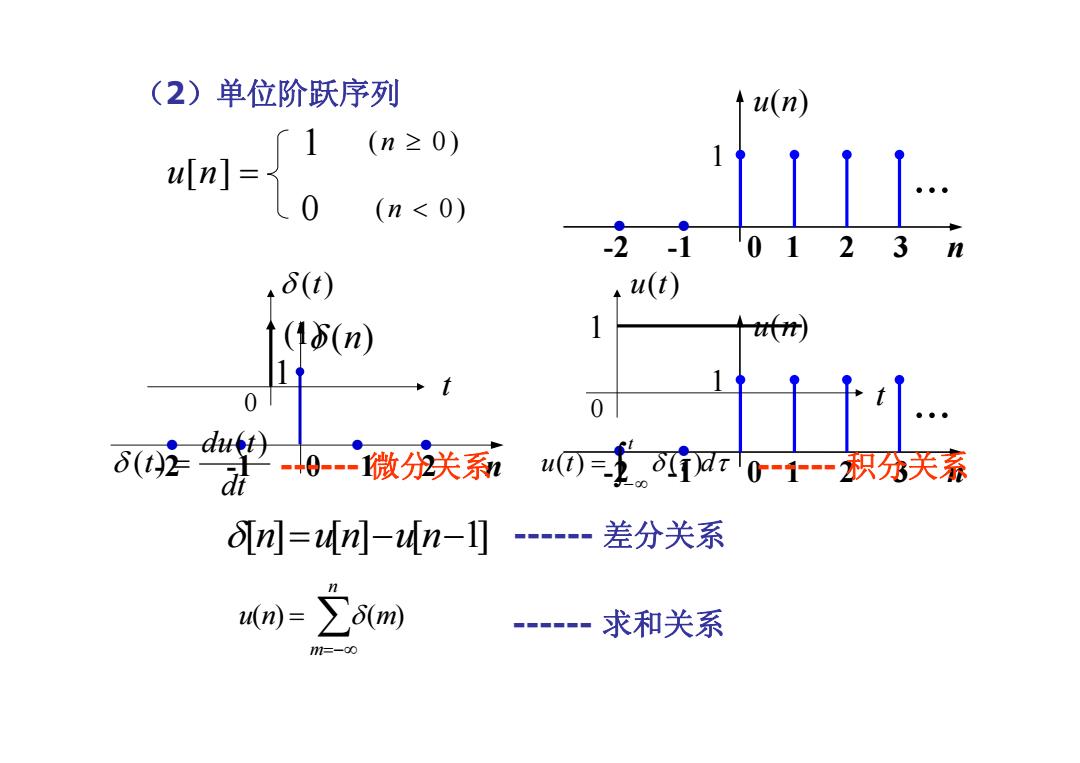
(2)单位阶跃序列 u(n) … 0123 6(t) u(t) (1b(n) ufn) 1 0 0 。t) 6©2-0㜫沃系 u0三王òr0-1中-积分关泰 n=m-4n-1]--差分关系 0m)=∑6m -求和关系 17=-c0
(2)单位阶跃序列 u n[ ] = 1 0 ( 0) n ≥ ( 0) n < ... -2 -1 0 1 2 3 n • • 1 u n( ) δ[ ] [ ] [ 1] n un un = −− ------ 差分关系 -2 -1 0 1 2 n • • • • δ ( ) n 1 ... -2 -1 0 1 2 3 n • • 1 u n( ) ∑ ------ 求和关系 =−∞ = n m u(n) δ(m) u(t) (1) 0 t t 1 0 δ (t) dt du t t ( ) δ ( ) = ------ 微分关系 u t δ τ dτ t ∫−∞ ( ) = ( ) ------ 积分关系
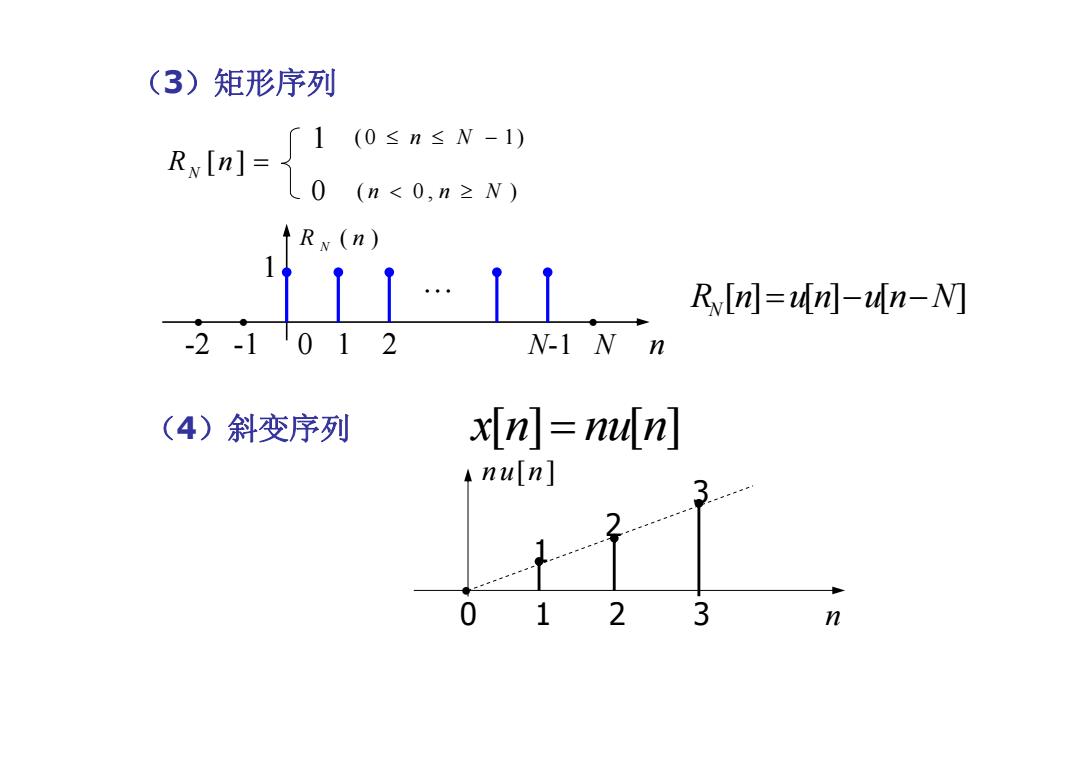
(3)矩形序列 R,lm川=10ss水-) 0 (n<0,n≥N) ↑Rx(n) 11…11 RyIn]=un]-un-N] -2-1012 N-1 N n (4)斜变序列 x[n]=4[n] nu n 0 1 2 3 n
[ ] R N n = 1 0 (0 1) ≤ n N ≤ − ( 0, ) n nN < ≥ (3)矩形序列 [] [] [ ] R n un un N N = − − (4)斜变序列 x n nu n [] [] = 0 1 2 3 n nu n[ ] • 1 2 3 ... -2 -1 0 1 2 N-1 N n • • • 1 ( ) R n N
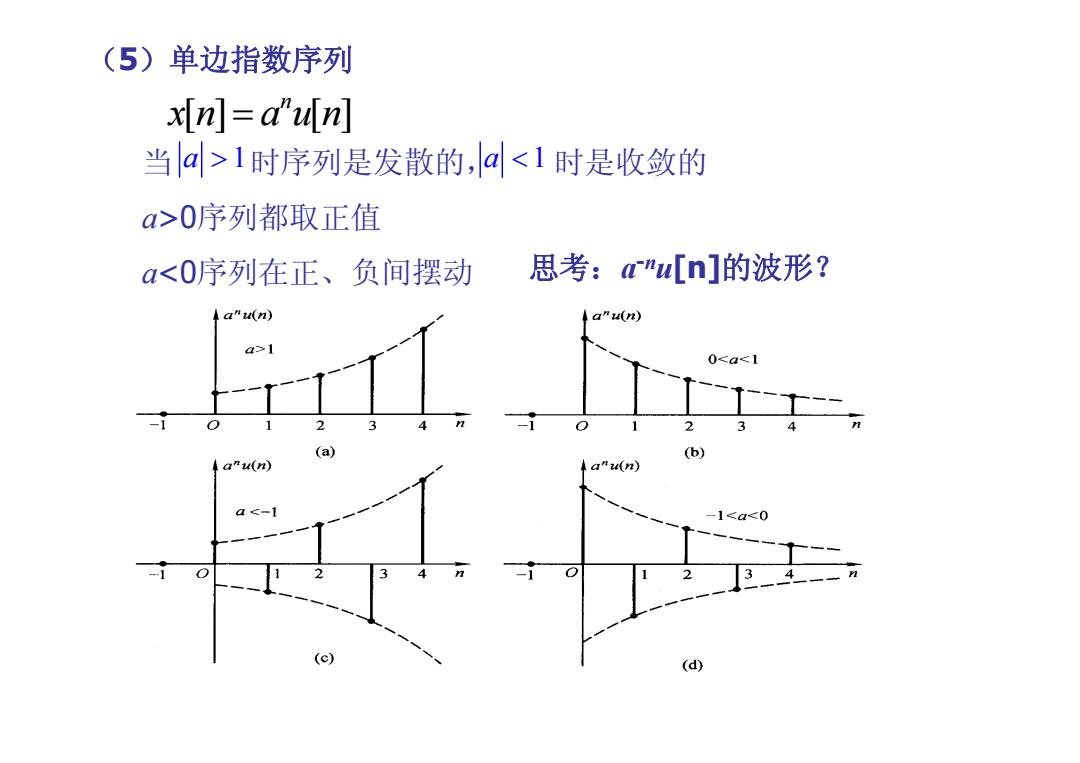
(5)单边指数序列 x[m=d”4n 当a>l时序列是发散的,a0序列都取正值 a1 0<a<1 -1 3 -1 2 3 (a) (b) a"u(n) A a"u(n) a<-1 -1<a<0 4 12 34- (c) (d)
(5)单边指数序列 [] [] n xn aun = 当 时序列是发散的, 时是收敛的 a>0序列都取正值 a 1 a < 1 思考:a-nu[n]的波形?
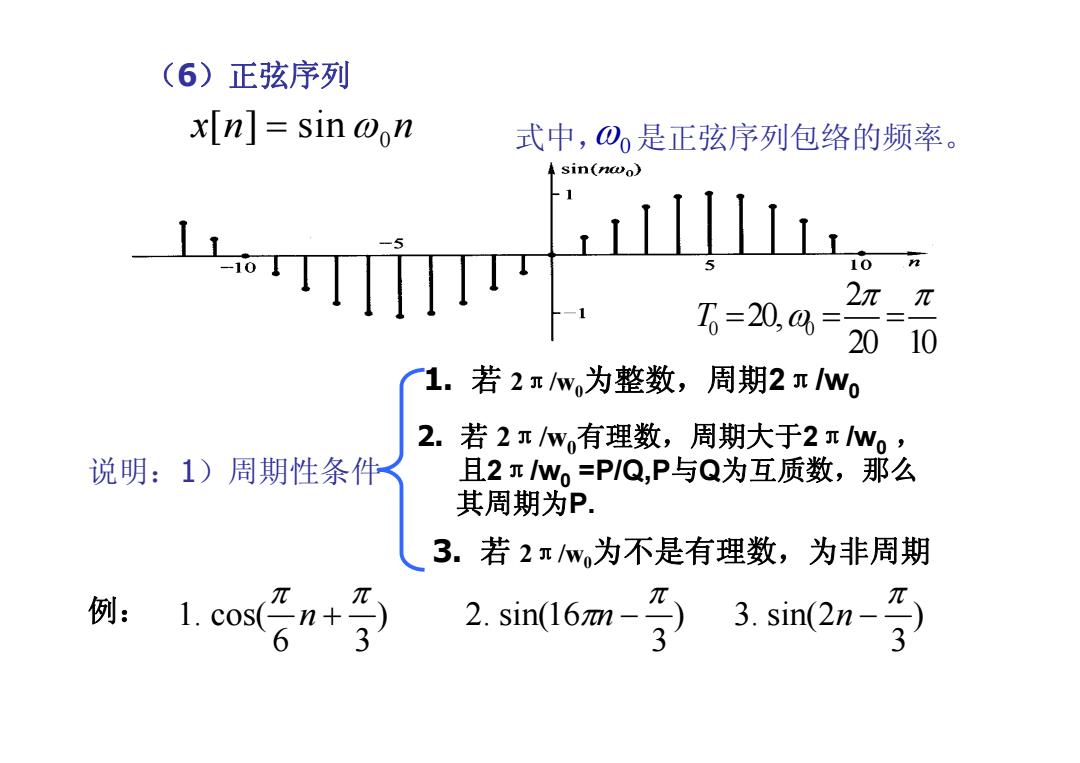
(6)正弦序列 x n sin@on 式中,①0是正弦序列包络的频率。 ◆sin(nwo) ILrrTiTITT 10 2π元 T=20,4= 2010 1.若2πw为整数,周期2TWo 2. 若2w有理数,周期大于2πWo, 说明:1)周期性条件< 且2πwo=P/Q,P与Q为互质数,那么 其周期为P. 3.若2πw为不是有理数,为非周期 例:1 1.co) 2.sin16am-令3sn(2n-7
(6)正弦序列 0 xn n [ ] sin = ω 式中, 是正弦序列包络的频率。 ω0 0 0 2 20, 20 10 T π π = == ω 说明:1)周期性条件 1. 若 2π/w0为整数,周期2π/w0 2. 若 2π/w0有理数,周期大于2π/w0 , 且2π/w0 =P/Q,P与Q为互质数,那么 其周期为P. 3. 若 2π/w0为不是有理数,为非周期 例: ) 6 3 1. cos(π π n + ) 3 2. sin(16 π πn − ) 3 3. sin(2 π n −

2)与连续系统正弦2关系: f(t)=sin(t) x[n]=f(nT)=sin(onT)=sin(no) @,=QT,©o为正弦序列频率,单位是弧度:Q 连续正弦频率,单位是弧度/秒。 (7)复指数序列 xIn]=e"cos@n+jsin con
2)与连续系统正弦 关系: Ω0 ( ) sin( ) 0 f t = Ω t 0 0 x n f nT nT n [ ] ( ) sin( ) sin( ) = =Ω = ω ,ω0为正弦序列频率,单位是弧度;Ω0为 连续正弦频率,单位是弧度/秒。 0 0 0 s T f ω Ω =Ω = (7)复指数序列 0 0 0 [ ] cos sin j n xn e n j n ω == + ω ω