《应用数学》课程教学大纲 浏览次数:155责任编辑:通讯作者:摄影: 一、 课程中文名称:应用数学 二、 课程英文名称:Applied Mathematics 三、 课程编码:ZB0620525 四、课程性质:专业必修课 五、学时数、学分数、开课学期 学时数:40学分数:2.5开课学期:第5学期 六、课程目的与要求 应用数学是水文与水资源工程专业的主要专业基础课,开设本课程的目的是:使学生能够运用应用数学的理论 把实际问题构建成数学模型,选择适当的优化方法,求出最优解或满意解,提高学生分析和解决实际问题的能力。 通过本课程的教学,要求学生掌握应用数学各主要分支的基本概念、数学模型及其求解方法,掌握应用数学整 体优化的思想和若干定量分析的优化技术。 七、本课程与其它课程的联系 应用数学以高等数学、线性代数、概率论与数理统计、计算机语言为先行课程,又是后续课程水资源管理的基 础。 八、教学方法:板书课堂讲授 九、考核方法:闭卷考试 十、选用教材及参考书目 教材:张莹.《运筹学基础》清华大学出版社,2005 参考书目: 2 《运筹学》教材编写组.《运筹学》(修订版)清华大学出版社,1994 2 胡运权.《运筹学基础及应用》.高等教育出版社,2004 2 胡运权.《运筹学习题集》清华大学出版社,2002 一、 教学进程安排表 学时 序号 章节教学内容 理论 实践 合计 线性规划 14 0 14 2 整数规划 4 0 4 3 目标规划 4 0 4 4 非线性规划 12 0 12 动态规划 6 0 6 合计 40 0 40 十二、主要教学内容、重点和难点 第一章线性规划 一、学习目的 通过本章的学习,掌握单纯形法、 改进单纯形法、对偶单纯形法、灵敏度分析,本章计划14学时。 二、 课程内容 第一节线性规划的数学模型 第二节图解法 第三节线性规划的基本概念和基本定理 第四节单纯形法 第五节改进单纯形法
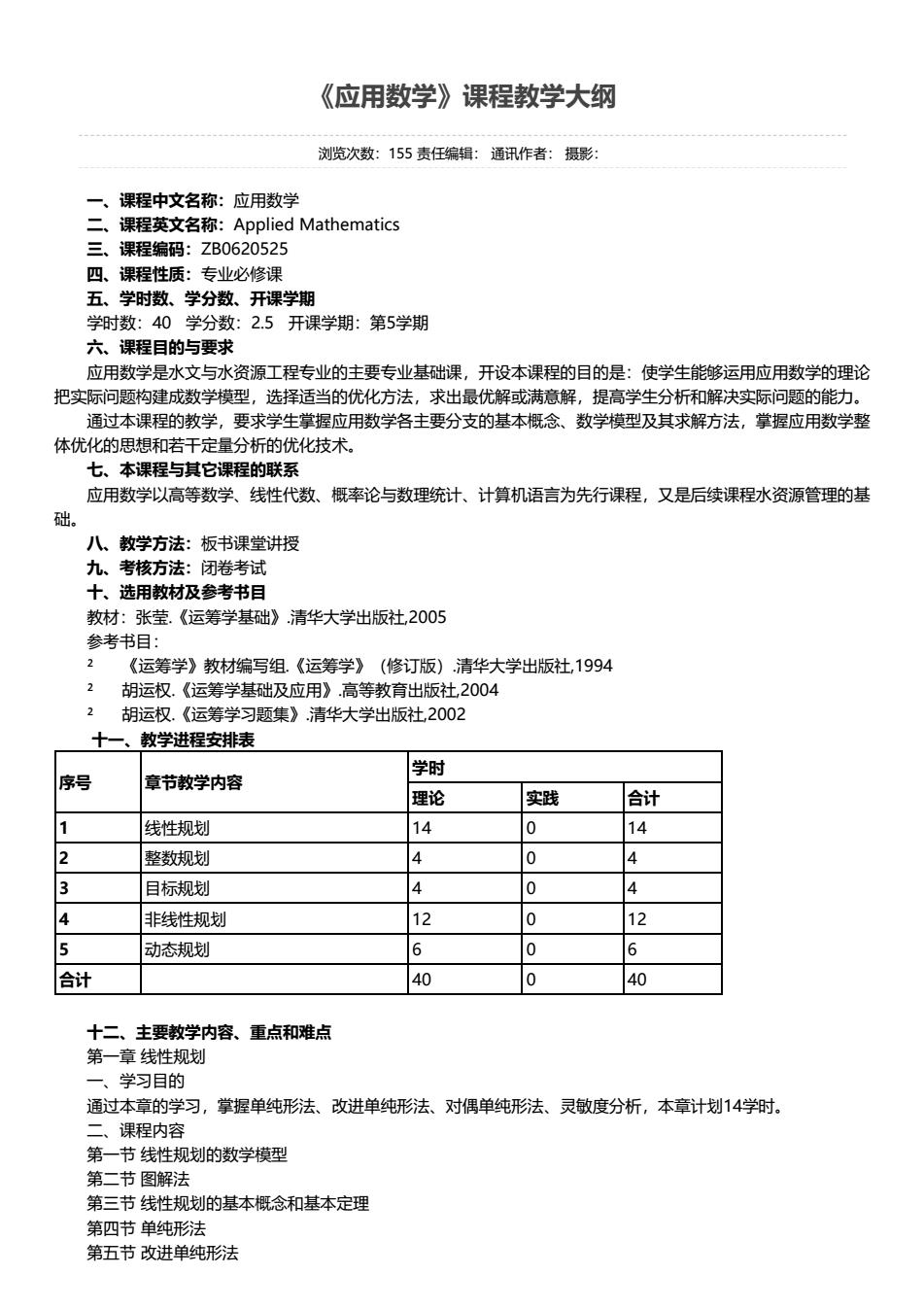
《应用数学》课程教学大纲 浏览次数:155 责任编辑: 通讯作者: 摄影: 一、课程中文名称:应用数学 二、课程英文名称:Applied Mathematics 三、课程编码:ZB0620525 四、课程性质:专业必修课 五、学时数、学分数、开课学期 学时数:40 学分数:2.5 开课学期:第5学期 六、课程目的与要求 应用数学是水文与水资源工程专业的主要专业基础课,开设本课程的目的是:使学生能够运用应用数学的理论 把实际问题构建成数学模型,选择适当的优化方法,求出最优解或满意解,提高学生分析和解决实际问题的能力。 通过本课程的教学,要求学生掌握应用数学各主要分支的基本概念、数学模型及其求解方法,掌握应用数学整 体优化的思想和若干定量分析的优化技术。 七、本课程与其它课程的联系 应用数学以高等数学、线性代数、概率论与数理统计、计算机语言为先行课程,又是后续课程水资源管理的基 础。 八、教学方法:板书课堂讲授 九、考核方法:闭卷考试 十、选用教材及参考书目 教材:张莹.《运筹学基础》.清华大学出版社,2005 参考书目: ² 《运筹学》教材编写组.《运筹学》(修订版).清华大学出版社,1994 ² 胡运权.《运筹学基础及应用》.高等教育出版社,2004 ² 胡运权.《运筹学习题集》.清华大学出版社,2002 十一、教学进程安排表 序号 章节教学内容 学时 理论 实践 合计 1 线性规划 14 0 14 2 整数规划 4 0 4 3 目标规划 4 0 4 4 非线性规划 12 0 12 5 动态规划 6 0 6 合计 40 0 40 十二、主要教学内容、重点和难点 第一章 线性规划 一、学习目的 通过本章的学习,掌握单纯形法、改进单纯形法、对偶单纯形法、灵敏度分析,本章计划14学时。 二、课程内容 第一节 线性规划的数学模型 第二节 图解法 第三节 线性规划的基本概念和基本定理 第四节 单纯形法 第五节 改进单纯形法

第六节线性规划的对偶理论 第七节对偶单纯形法 第八节灵敏度分析 三、重点、难点提示和教学手段 (一)教学重点 单纯形法的原理,单纯形表的计算方法,大M法,两阶段法,改进单纯形法计算步骤,对偶单纯形法计算步 骤,灵敏度分析。 (二)教学难点 单纯形表的计算方法,改进单纯形法计算步骤,对偶单纯形法计算步骤。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第二章整数规划 一、学习目的 通过本章的学习,掌握分枝定界法、割平面法、隐枚举法,本章计划4学时。 二、课程内容 第一节分枝定界法 第二节割平面法 第三节求解0-1规划的隐枚举法 三、重点、难点提示和教学手段 (一)教学重点 分枝定界法的计算方法和步骤,割平面法的计算方法和步骤。 (二)教学难点 0-1型整数规划变量的不可行性指标计算。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第三章目标规划 一、学习目的 通过本章的学习,掌握线性目标规划的图解法和单纯形法,本章计划4学时。 二、课程内容 第一节目标规划的基本概念和数学模型 第二节线性目标规划的图解法 第三节线性目标规划的单纯形法 三、重点、难点提示和教学手段 (一)教学重点 对实际问题如何建立目标规划的数学模型,如何用目标规划的单纯形法求解,对各种满意解的分析。 (二)教学难点 线性目标规划的单纯形法: (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第四章非线性规划 一、学习目的 通过本章的学习,掌握单变量函数的寻优方法、无约束条件下多变量函数寻优的各种方法、有约束条件下多变 量函数寻优的各种方法,本章计划12学时
第六节 线性规划的对偶理论 第七节 对偶单纯形法 第八节 灵敏度分析 三、重点、难点提示和教学手段 (一)教学重点 单纯形法的原理,单纯形表的计算方法,大M法,两阶段法,改进单纯形法计算步骤,对偶单纯形法计算步 骤,灵敏度分析。 (二)教学难点 单纯形表的计算方法,改进单纯形法计算步骤,对偶单纯形法计算步骤。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第二章 整数规划 一、学习目的 通过本章的学习,掌握分枝定界法、割平面法、隐枚举法,本章计划4学时。 二、课程内容 第一节 分枝定界法 第二节 割平面法 第三节 求解0-1规划的隐枚举法 三、重点、难点提示和教学手段 (一)教学重点 分枝定界法的计算方法和步骤,割平面法的计算方法和步骤。 (二)教学难点 0-1型整数规划变量的不可行性指标计算。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第三章 目标规划 一、学习目的 通过本章的学习,掌握线性目标规划的图解法和单纯形法,本章计划4学时。 二、课程内容 第一节 目标规划的基本概念和数学模型 第二节 线性目标规划的图解法 第三节 线性目标规划的单纯形法 三、重点、难点提示和教学手段 (一)教学重点 对实际问题如何建立目标规划的数学模型,如何用目标规划的单纯形法求解,对各种满意解的分析。 (二)教学难点 线性目标规划的单纯形法。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第四章 非线性规划 一、学习目的 通过本章的学习,掌握单变量函数的寻优方法、无约束条件下多变量函数寻优的各种方法、有约束条件下多变 量函数寻优的各种方法,本章计划12学时

二、课程内容 第一节非线性规划的数学模型和基本概念 第二节下降迭代算法 第三节单变量函数的寻优方法 第四节无约束条件下多变量函数的寻优方法 第五节有约束条件下多变量函数的寻优方法 三、重点、难点提示和教学手段 (一)教学重点 单变量函数的寻优方法,无约束条件下多变量函数寻优的各种方法,有约束条件下多变量函数寻优的各种方 法。 (二)教学难点 无约束条件下多变量函数寻优的各种方法,有约束条件下多变量函数寻优的各种方法。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第五章动态规划 一、学习目的 通过本章的学习,掌握一维确定性动态规划问题的寻优方法、二维离散和连续动态规划的寻优方法,本章计划 6学时。 二、课程内容 第一节动态规划的基本概念和模型构成 第二节动态规划的基本原理和基本方程 第三节一维确定性动态规划问题的寻优方法 第四节二维离散和连续动态规划的寻优方法 第五节动态规划方法的优点与限制 三、重点、难点提示和教学手段 (一)教学重点 动态规划顺序解法和逆序解法,若干典型问题动态规划模型及求解技巧。 (二)教学难点 二维离散和连续动态规划的寻优方法。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题
二、课程内容 第一节 非线性规划的数学模型和基本概念 第二节 下降迭代算法 第三节 单变量函数的寻优方法 第四节 无约束条件下多变量函数的寻优方法 第五节 有约束条件下多变量函数的寻优方法 三、重点、难点提示和教学手段 (一)教学重点 单变量函数的寻优方法,无约束条件下多变量函数寻优的各种方法,有约束条件下多变量函数寻优的各种方 法。 (二)教学难点 无约束条件下多变量函数寻优的各种方法,有约束条件下多变量函数寻优的各种方法。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题 第五章 动态规划 一、学习目的 通过本章的学习,掌握一维确定性动态规划问题的寻优方法、二维离散和连续动态规划的寻优方法,本章计划 6学时。 二、课程内容 第一节 动态规划的基本概念和模型构成 第二节 动态规划的基本原理和基本方程 第三节 一维确定性动态规划问题的寻优方法 第四节 二维离散和连续动态规划的寻优方法 第五节 动态规划方法的优点与限制 三、重点、难点提示和教学手段 (一)教学重点 动态规划顺序解法和逆序解法,若干典型问题动态规划模型及求解技巧。 (二)教学难点 二维离散和连续动态规划的寻优方法。 (三)教学手段及教学环节 板书课堂讲授 四、思考与练习 课后习题