
第七 堂 公 RZ40VMM 位移 Displacement method
第 十 一 章 位 移 法 Displacement method

§11-1位移法的基本概念 位移法的提出 从理论上讲,用力法可以分析各种(所 有)超静定结构。困难是当未知量较多时,力 法方程不易求解。这个困难对于计算工具落后 (无电子计算机)的年代,是一个很难解决的 问题 20世纪初,在力法的基础上提出了位移 法,位移法最主要的研究对象是高次超静定刚 架(多层多跨刚架)
§11-1 位移法的基本概念 一、位移法的提出 从理论上讲,用力法可以分析各种(所 有)超静定结构。困难是当未知量较多时,力 法方程不易求解。这个困难对于计算工具落后 (无电子计算机)的年代,是一个很难解决的 问题。 20世纪初,在力法的基础上提出了位移 法,位移法最主要的研究对象是高次超静定刚 架(多层多跨刚架)
基本设想:几何不变体系在一定外因荷载 支移、温改等)作用下,内力(反力)与变形之间 恒有一定关系。 Fp 0c 对应 确定的内力 确定的位移 位移法:先确定结构的某些结点位移, 再据此 确定其内力。基本未知量为结点位移
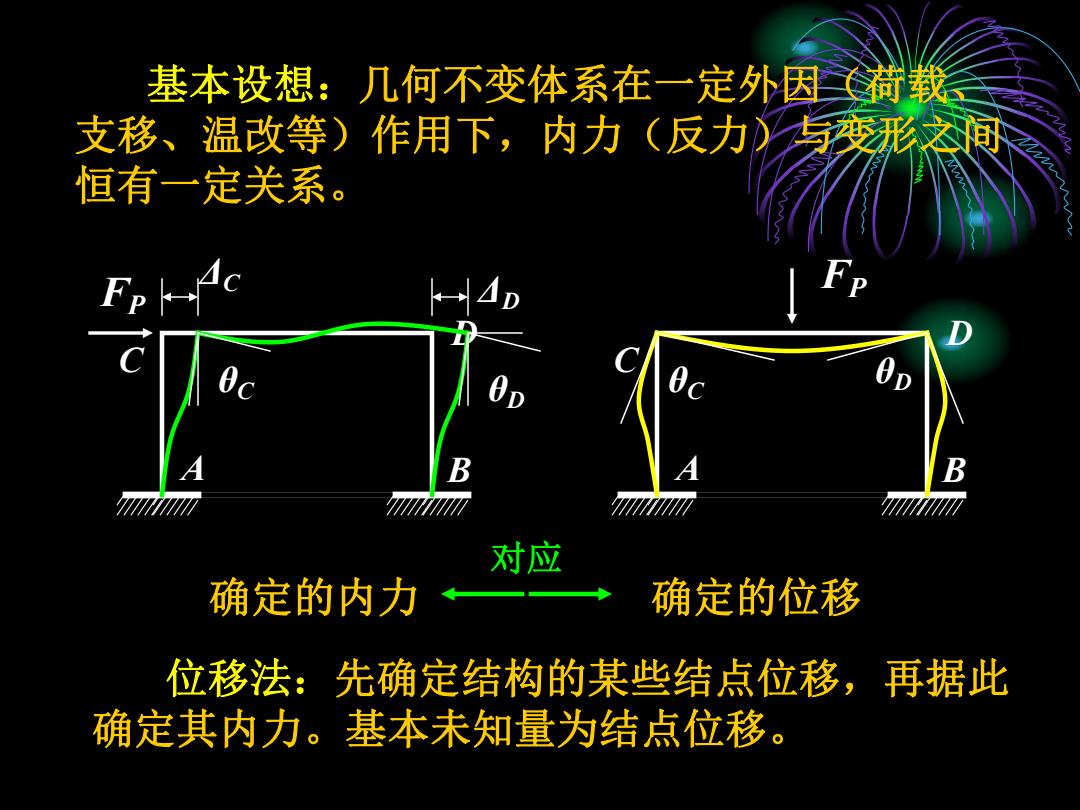
基本设想:几何不变体系在一定外因(荷载、 支移、温改等)作用下,内力(反力)与变形之间 恒有一定关系。 D A B C FP D A B C FP ΔC θC θD ΔD θC θD 确定的内力 确定的位移 对应 位移法:先确定结构的某些结点位移,再据此 确定其内力。基本未知量为结点位移

二、基本思路 B 06 MBA E=常数 ∑MB-0 MBA+M BC=0 I/2 I/2 2EI B 4E7 4E1 08 B 8
B C 二、基本思路 EI=常数 FP l/2 l/2 l C A B A B θB 3 BA B EI M l FP C B C B FP 8 F l P 8 F l P 4 B EI l 2 B EI l = + θB θB θB 4 8 P BC B EI F l M l B MBA MBC ∑MB=0 MBA+M BC =0

分析上图所示刚架 刚架在荷载作用下,发生黄线所示变 形。 其中,固端C,无任何位移; 铰支端A, 无线位移,只有铰位移;结点B,为刚结点 连接B结点的两杆杆端有相同的转角0B,忽 略轴向变形,认为无线位移。 讨论:如何确定每根杆件的内力? AB杆:可视为一端铰支,一端刚结的梁, 在B端发生杆端转角0B 杆端弯矩:Mg4=3EI0BI (a (杆端弯矩对杆端顺时针为正)
分析上图所示刚架 刚架在荷载作用下,发生黄线所示变 形。 其中,固端C,无任何位移;铰支端A, 无线位移,只有铰位移;结点B,为刚结点, 连接B结点的两杆杆端有相同的转角θB,忽 略轴向变形,认为无线位移。 讨论:如何确定每根杆件的内力? AB杆:可视为一端铰支,一端刚结的梁, 在B端发生杆端转角θB 杆端弯矩: MBA=3EIθB /l (a) (杆端弯矩对杆端顺时针为正)

BC杆:可将其视为两端刚结的梁,其 承受竖向荷载Fp,同时在B端发生转g 其杆端弯矩可由两部分叠加而成: M BC=-Fpl/8+4EI0B/(b) 同理:McB=+Fp8+2EI0sM 由(a)、(b)式可见,如0已知,则: MBA M EC、McB即可知,整个刚架的弯矩图 即可画出 因此,以0为基本未知量,并设法求出, 则各杆内力均可定出
BC杆:可将其视为两端刚结的梁,其上 承受竖向荷载FP ,同时在B 端发生转θB。 其杆端弯矩可由两部分叠加而成: M BC= -FP l /8+4EIθB /l (b) 同理: MCB = +FP l/8+2EIθB /l 由(a)、(b)式可见,如θB已知,则: MBA、 M BC、MCB即可知,整个刚架的弯矩图 即可画出。 因此,以θB为基本未知量,并设法求出, 则各杆内力均可定出

由平衡条件: 列结点B处,杆端弯矩应满足平衡条得 ∑MB=0 MBA+M BC=0 3EIOBA-Fpl/8+4EI@g/=0 (c) 7EI0B八-F8=0 0B=FpP/56EI 将0p代入(a)(b)式,则: MBA=3EI FpP/56EI =+3Fpl/56 M BC=-Fpl/8+4EI FpP/56EI=-3Fpl/56 MCB=+Fpl/8+2EIL FpR/56EI=+9Fpl/56
由平衡条件: 刚结点B处,杆端弯矩应满足平衡条件 ∑MB=0 MBA+M BC =0 3EIθB /l – FP l /8+4EIθB /l =0 (c) 7EIθB /l – FP l /8 =0 θB=FP l2 /56EI 将θB代入(a) (b)式,则: MBA= 3EI/l · FP l2 /56EI = +3FP l/56 M BC=-FP l/8+4EI/l · FP l2 /56EI = - 3FP l/56 MCB=+FP l/8+2EI/L · FP l2 /56EI = +9FP l/56

弯矩图如下图所示: MBA=+3Fpl/56 3Fp/56 Fpl/4 9F-/56 B MBC=-3Fpl/56 MCB=+9Fpl/56
弯矩图如下图所示: 3FP l/56 9FP F l/56 P l /4 MBA= +3FP l/56 MBC= - 3FP l/56 MCB= +9FP l/56

由简例可见位移法的基本思路 (1)根据结构的几何条件(包括变形连续条 件和边界支承条件)确定某些结点位移作为 基本未知量 (2)把每根杆件视为单跨超静定杆,建立其 杆端内力与杆端位移、荷载之间的关系。 (3)根据平衡条件求解结点位移。 (4)结点位移代入杆端内力公式解出最后 内力 (变形协调 平衡条件) 原结构 若干根杆件 整体结构 拆 搭 (还原)
由简例可见位移法的基本思路: (1) 根据结构的几何条件(包括变形连续条 件和边界支承条件)确定某些结点位移作为 基本未知量。 (2) 把每根杆件视为单跨超静定杆,建立其 杆端内力与杆端位移、荷载之间的关系。 (3) 根据平衡条件求解结点位移。 (4) 结点位移代入杆端内力公式解出最后 内力。 整体结构 (变形协调) 拆 搭 (还原) 原结构 若干根杆件 (平衡条件)

三、需解决的问题 1、单跨(超静定)杆件在杆端发生 各种位移作用下的杆端力,以及单跨杆 在各种外因(包括荷载等因素)作用下 的杆端力。 2、讨论结构上的哪些结点位移作为 基本未知量。 3、位移法方程的建立及其求解
三、需解决的问题 1、单跨(超静定)杆件在杆端发生 各种位移作用下的杆端力,以及单跨杆 在各种外因(包括荷载等因素)作用下 的杆端力。 2、讨论结构上的哪些结点位移作为 基本未知量。 3、位移法方程的建立及其求解