
第 章 结构的几何组成分析
结构的几何组成分析 第 二 章

§2.1几何构造分析的几个概念 体系一杆件十约 束(联系) 杆件:不考虑材料弹性 应变,视作列体,平面 刚体称为“刚片”。 约束:限制刚片运动的 装置
§2.1 几何构造分析的几个概念 一.体系——杆件+约 束(联系) 杆件:不考虑材料弹性 应变,视作刚体,平面 刚体称为“刚片” 。 约束:限制刚片运动的 装置
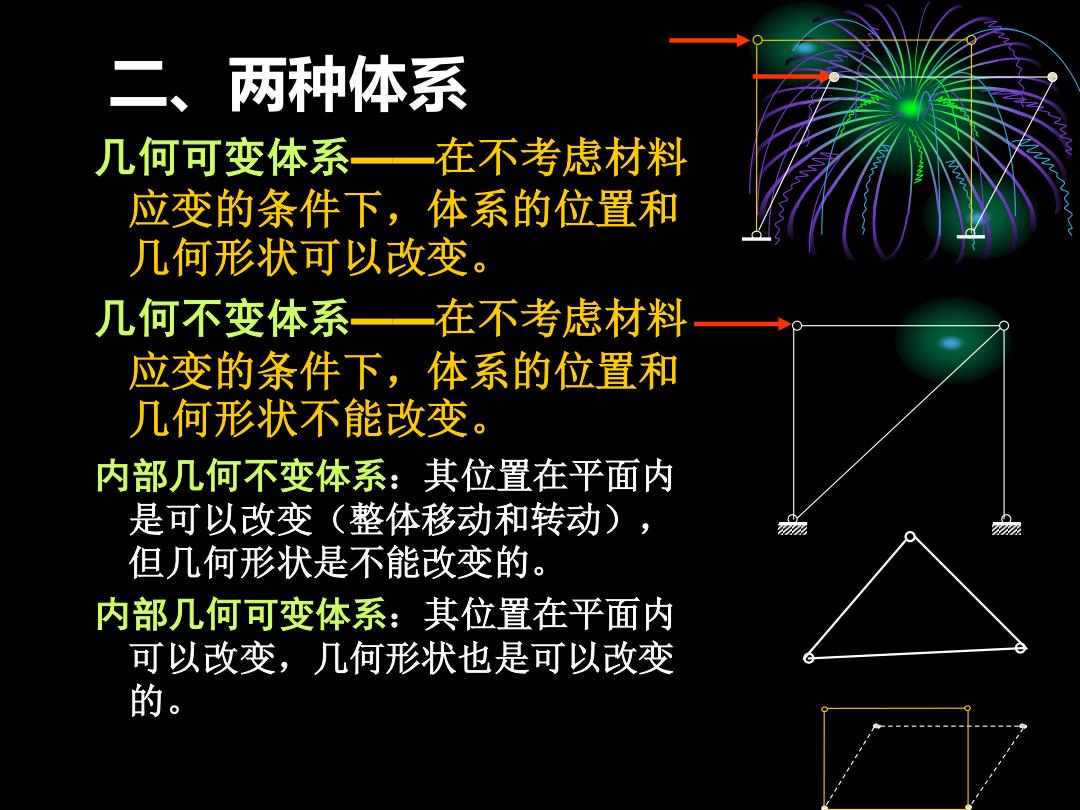
二、两种体系 几何可变体系一在不考虑材料 应变的条件下,体系的位置和 几何形状可以改变。 几何不变体系一在不考虑材料 应变的条件下,体系的位置和 几何形状不能改变。 内部几何不变体系:其位置在平面内 是可以改变(整体移动和转动), 但几何形状是不能改变的。 内部几何可变体系:其位置在平面内 可以改变,几何形状也是可以改变 的
二、两种体系 几何可变体系——在不考虑材料 应变的条件下,体系的位置和 几何形状可以改变。 几何不变体系——在不考虑材料 应变的条件下,体系的位置和 几何形状不能改变。 内部几何不变体系:其位置在平面内 是可以改变(整体移动和转动), 但几何形状是不能改变的。 内部几何可变体系:其位置在平面内 可以改变,几何形状也是可以改变 的

杆系体系几何组成分析的目的 (1)检查并保证结构的几何不变性。 体系是否可做结构?并创造新颗合理的结构 形式) (2)研究几何不变体系的组成规则,区分静 定结构和超静定结构。 (3)指导结构的内力计算(几何组成分析 与内力分析之间有密切联系)
杆系体系几何组成分析的目的 (1)检查并保证结构的几何不变性。( 体系是否可做结构? 并创造新颖合理的结构 形式) (2)研究几何不变体系的组成规则,区分静 定结构和超静定结构。 (3)指导结构的内力计算(几何组成分析 与内力分析之间有密切联系)

三、自由度 体系的运动自由度=体系独立运动 的数目或体系运动时可以独立改变的 坐标数目。 自由度是度量体系是否运动的数 量标志,有自由度的体系必然运动, 自由度等于零的体系可能不运动
三、自由度 • 体系的运动自由度=体系独立运动 的数目或体系运动时可以独立改变的 坐标数目。 • 自由度是度量体系是否运动的数 量标志,有自由度的体系必然运动, 自由度等于零的体系可能不运动

1、平面内一个自由的 点 平面内一个自由的点有两 个自由度。 S=2 △x 即:由两个独立的坐标可 唯一地确定这个点的位置
1、平面内一个自由的 点 平面内一个自由的点有两 个自由度。 S = 2 即:由两个独立的坐标可 唯一地确定这个点的位置。 A A' D x D y y 0 x
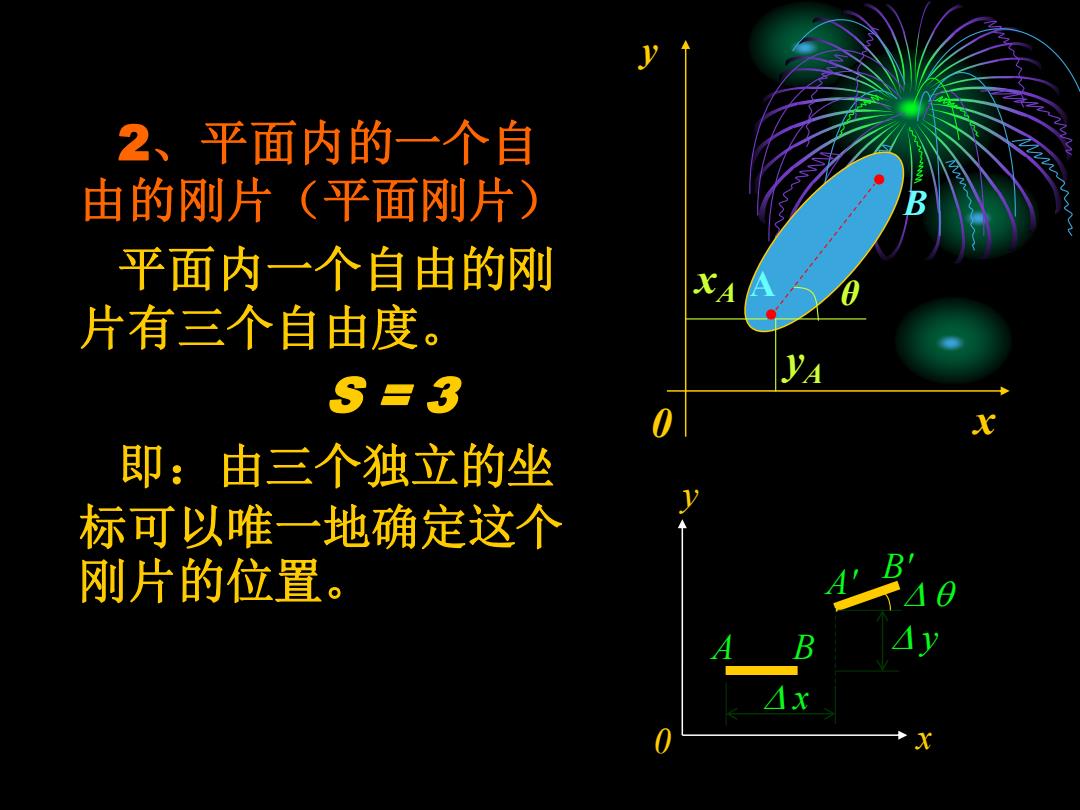
2、平面内的一个自 多多 由的刚片(平面列片) B 平面内一个自由的列 XA 片有三个自由度。 S=3 即:由三个独立的坐 标可以唯一地确定这个 刚片的位置。 1
2、平面内的一个自 由的刚片(平面刚片) 平面内一个自由的刚 片有三个自由度。 S = 3 即:由三个独立的坐 标可以唯一地确定这个 刚片的位置。 x y 0 xA A yA B θ A B A' B' D x D y D y 0 x

四、约束(联系)一限制(或减少 运动自由度的装置 (一)支座约束 链杆一两端是铰的刚性杆件。 被约束物体不能沿链杆方向移 动,减少了被约束物体的一个 运动自由度。 根链杆=一个约束 一 1、滚轴支座 B 减少一个自由度,相当一个约束
四、约束(联系)— 限制(或减少) 运动自由度的装置 链杆 — 两端是铰的刚性杆件。 被约束物体不能沿链杆方向移 动,减少了被约束物体的一个 运动自由度。 一根链杆=一个约束。 1、滚轴支座 减少一个自由度,相当一个约束。 A (一)支座约束 B A C B

2、铰支座 减少两个自由度,相当两个约束。 3、固定支座 使刚片的自由度减少为零,相当于三个约束。 (二)刚片间的连接约束 1、链杆 两个刚片相互之间有三个自由度,用链杆连接 后,沿链杆方向的移动受到约束,相互之间自 由度减少一个
2、铰支座 减少两个自由度,相当两个约束。 3、固定支座 使刚片的自由度减少为零,相当于三个约束。 (二)刚片间的连接约束 1、链杆 两个刚片相互之间有三个自由度,用链杆连接 后,沿链杆方向的移动受到约束,相互之间自 由度减少一个

2、单铰一联结两刚片 的圆柱铰。 被约束物体在单铰联结处 不能有任何相对移动,只有 绕铰的相对转动,相互之间 自由度减少了两个。 一个单铰=两个约束=两根 链杆。 3、简单刚结 两列片间没有相对运动,使 相互之间自由度减少了三个。 一个简单刚结=三个约束
2、单铰 — 联结两刚片 的圆柱铰。 被约束物体在单铰联结处 不能有任何相对移动,只有 绕铰的相对转动,相互之间 自由度减少了两个。 一个单铰 =两个约束 =两根 链杆。 3、简单刚结 两刚片间没有相对运动,使 相互之间自由度减少了三个。 一个简单刚结 =三个约束。 Ⅰ A Ⅱ