
感 静定刚架
第 四 章 静定刚架

§4-1静定平面刚架的几何组成及特点 一、 平面列架的特点 1、刚架:由梁柱相互刚结(或部分铰接)组 成,主要由刚结点维持的几何不变的体系。 优点:结构整体性好,刚度大,内力分布较均 匀合理,净空大,应用广 下图是常见的几种刚架:图()是车站雨蓬, 图(b)是多层多跨房屋,图(c)是具有部分铰结 点的刚架
§4-1 静定平面刚架的几何组成及特点 一、平面刚架的特点 1、刚架:由梁柱相互刚结(或部分铰接)组 成,主要由刚结点维持的几何不变的体系。 优点:结构整体性好,刚度大,内力分布较均 匀合理,净空大,应用广。 下图是常见的几种刚架:图(a)是车站雨蓬, 图(b)是多层多跨房屋,图(c)是具有部分铰结 点的刚架
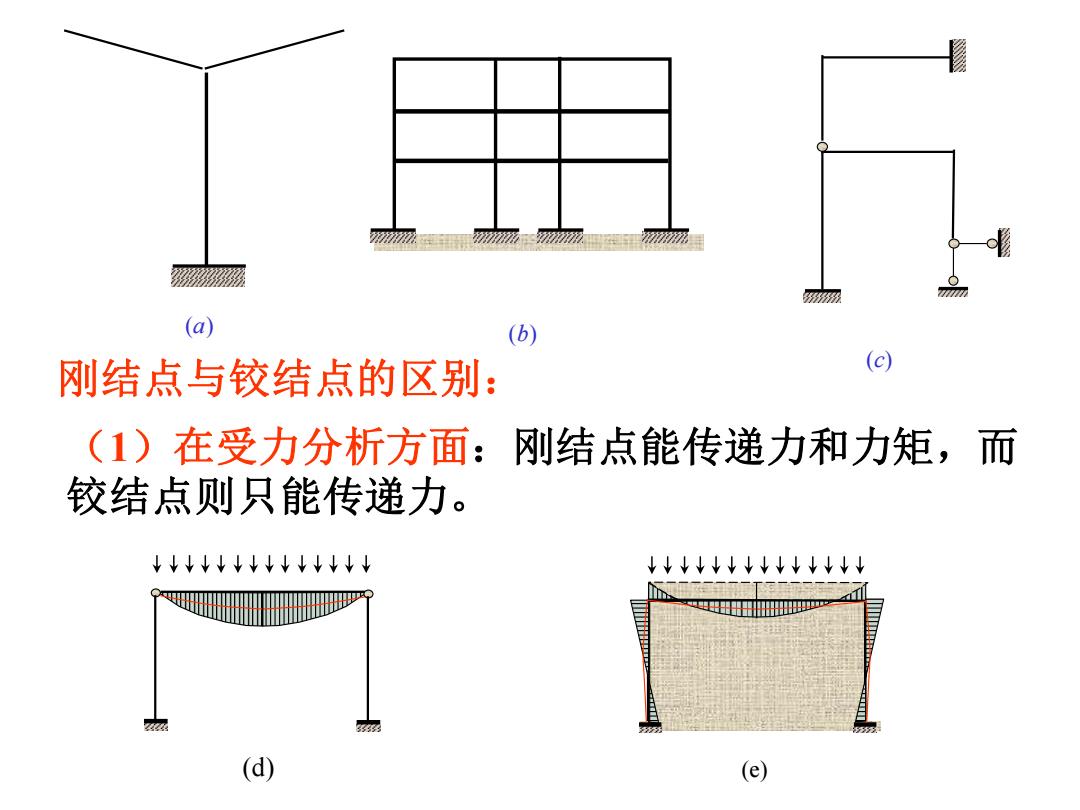
(a) (b) 刚结点与铰结点的区别: (c) (1)在受力分析方面:刚结点能传递力和力矩,而 铰结点则只能传递力。 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓ ↓↓↓↓↓↓↓↓↓↓↓↓ 2 (d) (e)
(a) (b) (c) (d) (e) 刚结点与铰结点的区别: (1)在受力分析方面:刚结点能传递力和力矩,而 铰结点则只能传递力
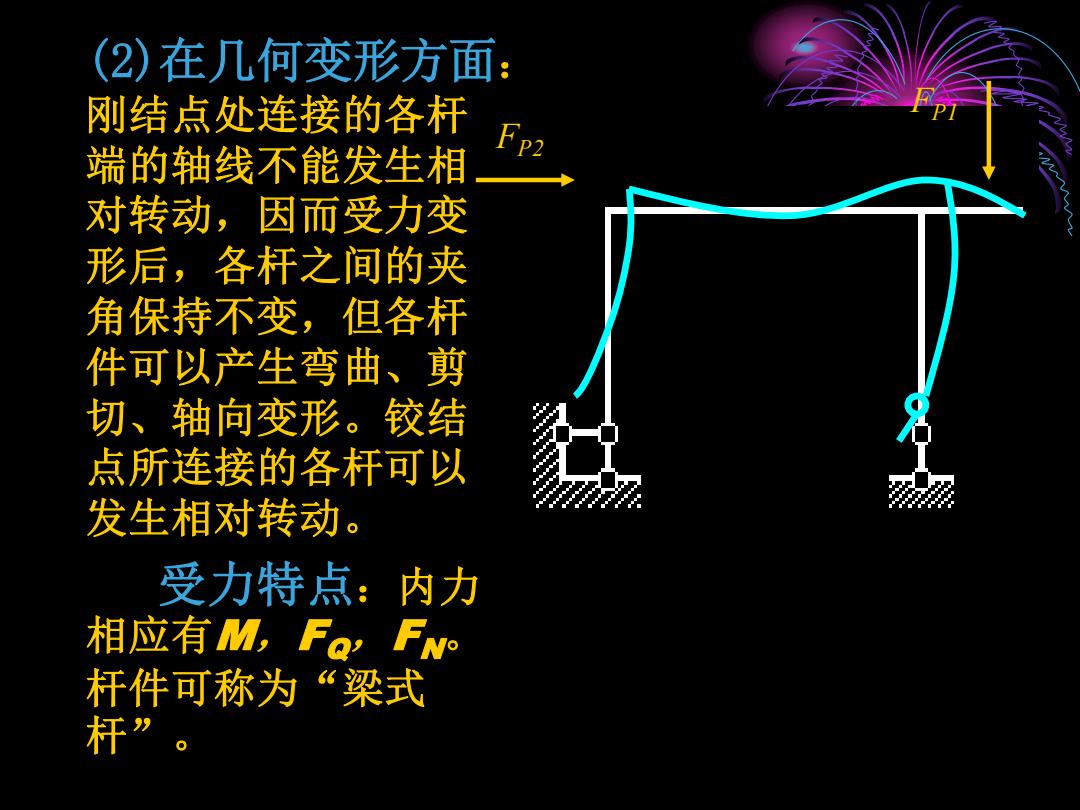
(2)在几何变形方面 刚结点处连接的各杆 端的轴线不能发生相 Fp2 对转动,因而受力变 形后,各杆之间的夹 角保持不变,但各杆 件可以产生弯曲、剪 切、轴向变形。铰结 点所连接的各杆可以 发生相对转动。 受力特点:内力 相应有M,FaFN 杆件可称为“梁式 杆
(2)在几何变形方面 : 刚结点处连接的各杆 端的轴线不能发生相 对转动,因而受力变 形后,各杆之间的夹 角保持不变,但各杆 件可以产生弯曲、剪 切、轴向变形。铰结 点所连接的各杆可以 发生相对转动。 受力特点:内力 相应有 M, FQ, FN 。 杆件可称为 “梁式 杆 ” 。 FP1 FP2

二、常见的静定平面刚架类型 1、悬臂刚架 2、简支刚架 3、三铰刚架 5、多层刚架 4、多跨刚架
1、悬臂刚架 2、简支刚架 3、三铰刚架 4、多跨刚架 二、常见的静定平面刚架类型 5、多层刚架

§4-2静定刚架支座反力的计算 刚架分析的步骤一般是先求出支座反力,再 求出各杆控制截面的内力,然后再绘制各杆的 弯矩图和刚架的内力图。 简支刚架和悬臂刚架支座反力计算较简单 这里主要讨论三铰刚架和多跨刚架的支座反力 计算。 在支座反力的计算过程中,应尽可能建立独 立方程
刚架分析的步骤一般是先求出支座反力,再 求出各杆控制截面的内力,然后再绘制各杆的 弯矩图和刚架的内力图。 简支刚架和悬臂刚架支座反力计算较简单, 这里主要讨论三铰刚架和多跨刚架的支座反力 计算。 在支座反力的计算过程中,应尽可能建立独 立方程。 §4-2 静定刚架支座反力的计算
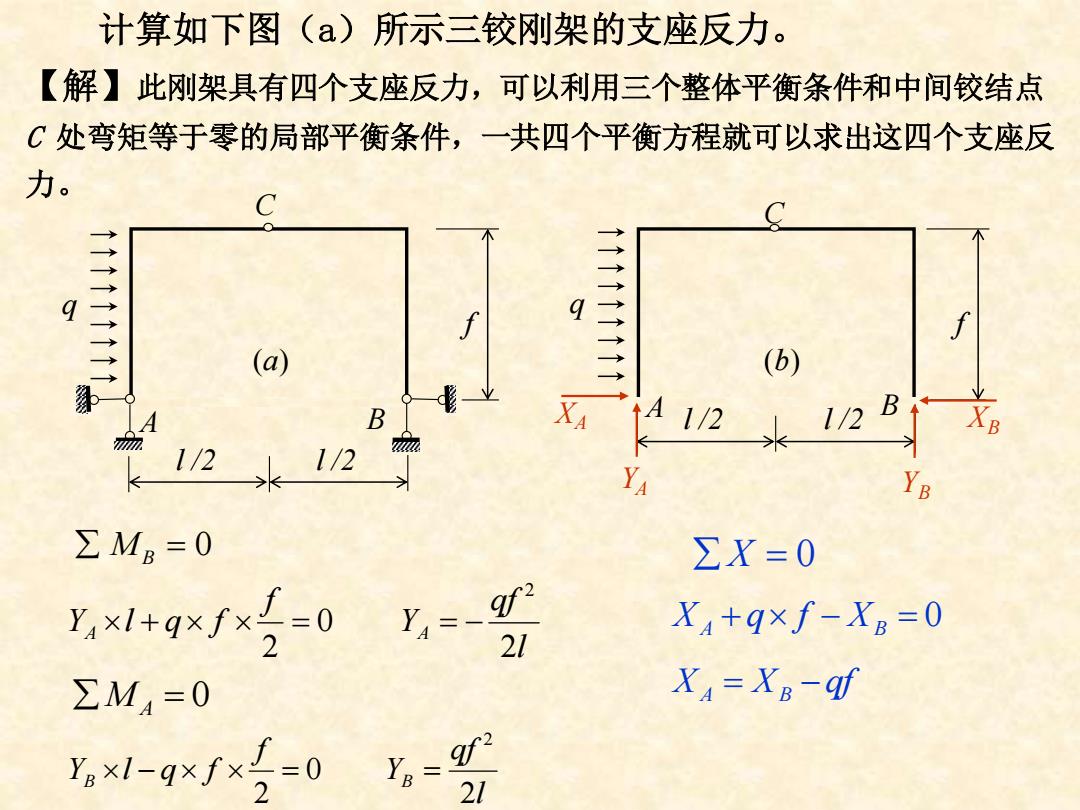
计算如下图(a)所示三铰刚架的支座反力。 【解】此刚架具有四个支座反力,可以利用三个整体平衡条件和中间铰结点 C处弯矩等于零的局部平衡条件,一共四个平衡方程就可以求出这四个支座反 力。 C 111111111 f (a) 111111I (b) 业 B XA tA1/2 1/2 1/2 1/2 Ya YB ∑Mg=0 ΣX=0 yx1+gxf×3=0 Y4=- X4+q×f-XB=0 21 ∑M4=0 X4=XB一9时 Yxl-qxfxj-0 Ya= 21
计算如下图(a)所示三铰刚架的支座反力。 【解】此刚架具有四个支座反力,可以利用三个整体平衡条件和中间铰结点 C 处弯矩等于零的局部平衡条件,一共四个平衡方程就可以求出这四个支座反 力。 XA MB = 0 l qf Y f Y l q f A A 2 0 2 2 + = = − MA = 0 l qf Y f Y l q f B B 2 0 2 2 − = = X = 0 XA + q f − XB = 0 X X qf A = B − l /2 l /2 q A B C f (a) q f l /2 l /2 A B C (b) YA YB XB

C B 111111111 1/2 立B f (c) XA 1/2 1/2 B XB 对O点取矩即得: YA YB (b) ∑M。=0 ,24a马=0 X4=Xa-q功 ∑Mc=0 X2×f-X0 X=-4 X 多跨刚架支座反力计算见 于是X4=一4 P44例4.2
XA q f l /2 l /2 A B C (b) YA YB XB f l /2 C (c) YB XB B XC YC MC = 0 0 2 − = l XB f YB 4 qf XB = 于是 X qf A 4 3 = − X X qf A = B − O 对O点取矩即得: MO = 0 0 2 3 2 + = f X f qf A X qf A 4 3 = − 多跨刚架支座反力计算见 P44例4.2

§4-3用截面法求静定刚架杆端截面内力 1、刚架的内力及正负号规定 弯矩M一不规定正负方向,弯矩图纵坐标 画在杆件受拉纤维一边。 剪力Q一规定同材力。 轴力N一规定同材力 2、刚结点处的杆端截面及杆端截面内力的 表示方法 内力符号双脚标,两个字母表示两个杆 端,第一个字母表示杆端力是哪一端的,第 二个字母表示杆远端的标号。如M4B为AB杆 A端的弯矩
§4-3 用截面法求静定刚架杆端截面内力 1、刚架的内力及正负号规定 弯矩M —不规定正负方向,弯矩图纵坐标 画在杆件受拉纤维一边。 剪力Q —规定同材力。 轴力N —规定同材力。 2、刚结点处的杆端截面及杆端截面内力的 表示方法 内力符号双脚标,两个字母表示两个杆 端,第一个字母表示杆端力是哪一端的,第 二个字母表示杆远端的标号。如MAB为AB杆 A端的弯矩

3、杆端截面内力计算 每一个杆件有两个杆端截面沿杆端截 面截开,在截开的截面处有三个未知内为 M、 Q、N,Q和N按正方向画,M可按任意 假设方向画,一般假设未知M按顺时针旋 转方向画。如计算结果为正,讠 说明内力方 向与图中方向相同;否则,与图中方向相 反。 4、 刚结点处力和力矩的平衡校核 刚结点上各杆端截面的内力应满足三个 平衡条件: ∑X=0∑Y=0 ΣM=0 用以校核杆件内力的计算结果。见P47例4.3
3、杆端截面内力计算 每一个杆件有两个杆端截面,沿杆端截 面截开,在截开的截面处有三个未知内力 M、Q、N,Q和N按正方向画,M可按任意 假设方向画,一般假设未知M按顺时针旋 转方向画。如计算结果为正,说明内力方 向与图中方向相同;否则,与图中方向相 反。 4、刚结点处力和力矩的平衡校核 刚结点上各杆端截面的内力应满足三个 平衡条件: ΣX=0 ΣY=0 ΣM=0 用以校核杆件内力的计算结果。见P47例4.3