
设空间有一个四面体,顶点A,B C,D的坐标依次是((0,0,0),( 2, 0,1),(4,0,0),(3,2,1)从z轴 正向无穷远处观察,求各面的可见性 观察方向向量是k=(0,0,1),三角 面DAB的法向量是: n=DA×AB=(-3,-2,-1)×(2,0, =(-2,1,4④
设空间有一个四面体,顶点A,B, C,D的坐标依次是(0,0,0),(2, 0,1),(4,0,0),(3,2,1)从z轴 正向无穷远处观察,求各面的可见性 观察方向向量是k=(0,0,1),三角 面DAB的法向量是: ( ) ( ) ( 2,1,4) n D A A B 3 , 2 , 1 2,0,1 = − = = − − −
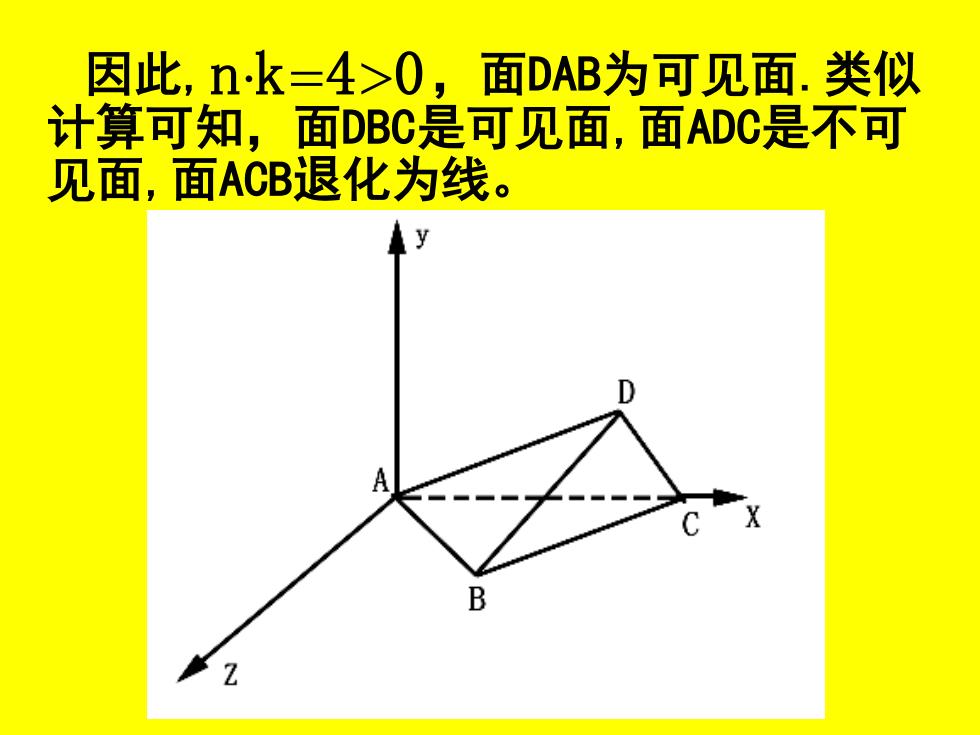
因此,n·k=4>0,面DAB为可见面.类似 计算可知,面DBC是可见面,面ADC是不可 见面,面ACB退化为线。 A
因此, ,面DAB为可见面.类似 计算可知,面DBC是可见面,面ADC是不可 见面,面ACB退化为线。 nk=40

利用外法线就可以判断凸多面体上 各表面的可见性,由此就能解决对单个 凸多面体的隐藏线和隐藏面的消除问题。 消除隐藏线的线面比较法的最先一 步就是利用外法线判断出所有可能的可 见面,可能可见面上的线段是可能可见 线。要依次用每一条可能可见线,与每 一个可能可见面比较,从而确定出可见 线、隐藏线及可见线上的隐藏部分
利用外法线就可以判断凸多面体上 各表面的可见性,由此就能解决对单个 凸多面体的隐藏线和隐藏面的消除问题。 消除隐藏线的线面比较法的最先一 步就是利用外法线判断出所有可能的可 见面,可能可见面上的线段是可能可见 线。要依次用每一条可能可见线,与每 一个可能可见面比较,从而确定出可见 线、隐藏线及可见线上的隐藏部分
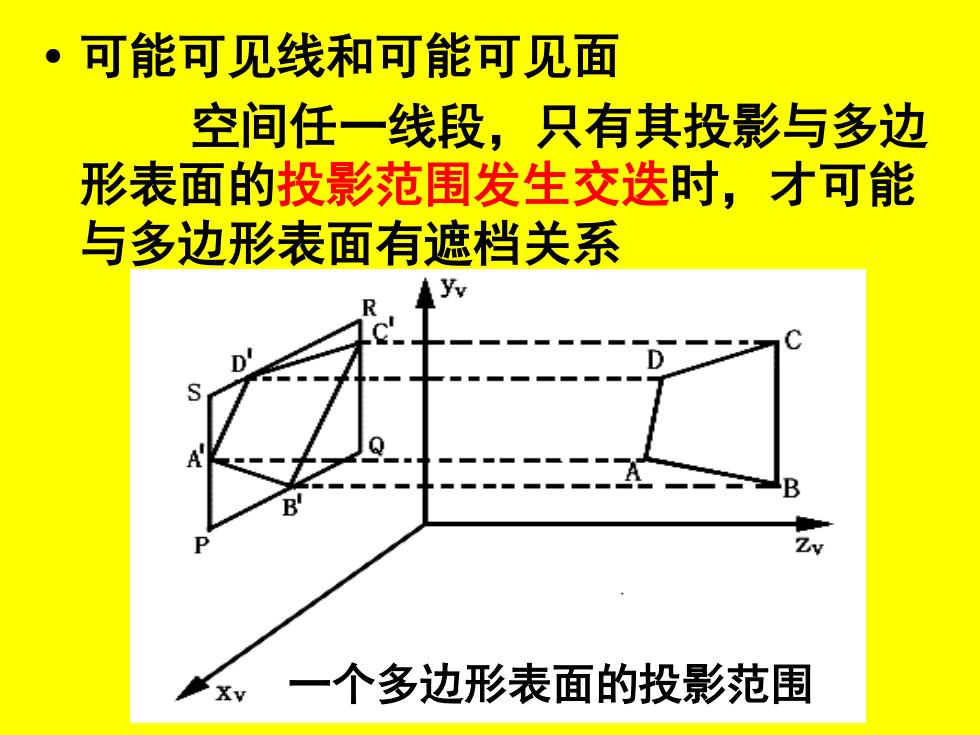
·可能可见线和可能可见面 空间任一线段,只有其投影与多边 形表面的投影范围发生交迭时,才可能 与多边形表面有遮档关系 一个多边形表面的投影范围
• 可能可见线和可能可见面 空间任一线段,只有其投影与多边 形表面的投影范围发生交迭时,才可能 与多边形表面有遮档关系 一个多边形表面的投影范围

范围检查也称为最大最小检验,即通过 比较有关的最大或最小值来判定范围的 交迭情形。 B
• 范围检查也称为最大最小检验,即通过 比较有关的最大或最小值来判定范围的 交迭情形

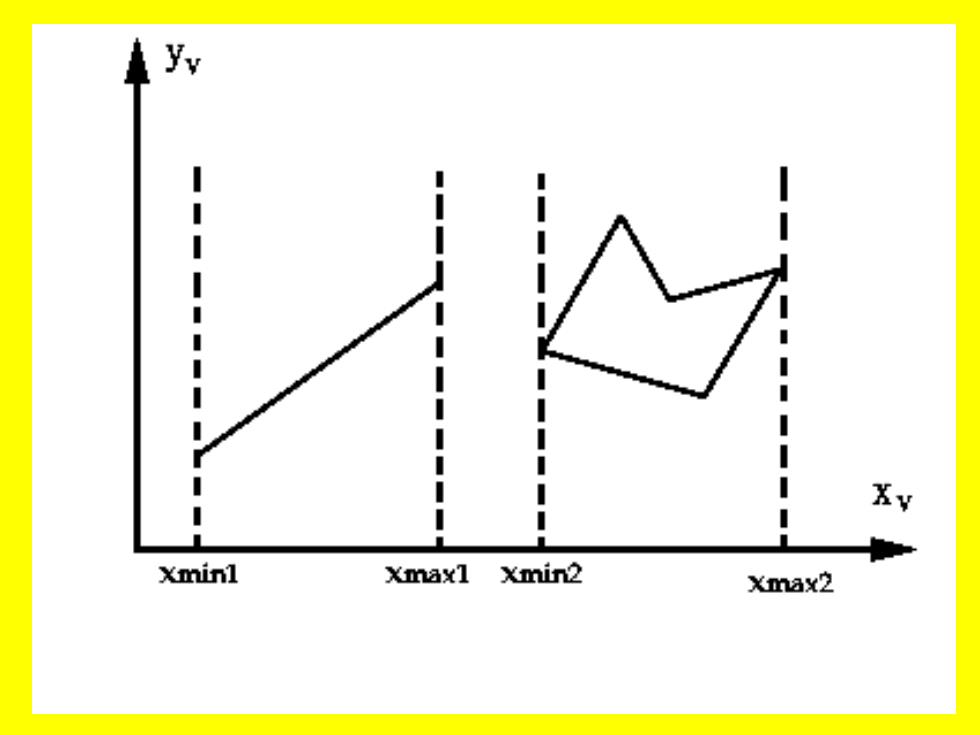
按X方向对投影范围的检查,可分别 计算出投影线段和多边形表面投影范围X 坐标的最大值和最小值,设分别是 Xmax1'XminlXmax2Xmin2 于是若Xa1≤Xin2或者Xax2≤Xin1,线 段和多边形表面就必然没有遮挡关系。 显然按x方向或按yv方向都可以类似地 做范围检查,这时可避免消除隐藏面时很 多不必要的深度比较
按Xv方向对投影范围的检查,可分别 计算出投影线段和多边形表面投影范围X 坐标的最大值和最小值,设分别是 min2 ,x max2 ,x min1 ,x max1 x 于是若 ≤ 或者 ≤ ,线 段和多边形表面就必然没有遮挡关系。 显然按xv方向或按yv方向都可以类似地 做范围检查,这时可避免消除隐藏面时很 多不必要的深度比较。 xmax1 min2 x xmax2 min1 x
Xy Xminl Xmaxl Xmin2 Xmax2

z方向的范围检查是沿z方向观 察时粗略的深度检验。 在此范围检查中若线段投影的最 大z坐标Zax小于多边形表面投影范 围最小的z坐标乙i2,则线段完全 在表面前面,根本不发生遮挡现象, 可以不必再往下做精确的深度检验
zv方向的范围检查是沿zv方向观 察时粗略的深度检验。 在此范围检查中若线段投影的最 大z坐标 小于多边形表面投影范 围最小的z坐标 ,则线段完全 在表面前面,根本不发生遮挡现象, 可以不必再往下做精确的深度检验。 m i n 2 z m a x 1 z
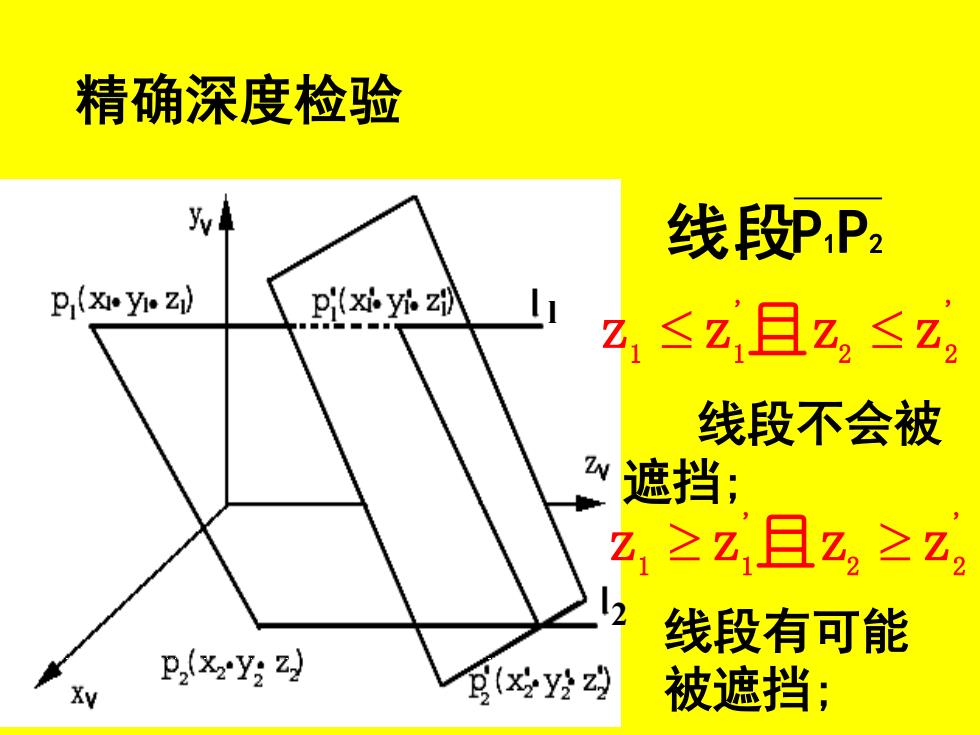
精确深度检验 w 线段P2 P (xIyi Zi) 米z Z≤z,且z2≤z2 线段不会被 遮挡; 2,≥Z且Z,≥Z2 线段有可能 D.(x2Y:Z) (x女y经 被遮挡;
精确深度检验 线段P1P2 l 2 ' 2 2 ' z1 z1 且 z z 线段不会被 遮挡; ' 2 2 ' z1 z1 且 z z 线段有可能 被遮挡;

求交点 Ax+By+Cz+D-0 直线L的参数方程可写成X=x1,Yy1, Z=2+t,代入平面方程得: AX+By1+C(z1+t)+D-0 解得t=-Ax1+By1+CZ1+D
求交点 A x+B y+C z+D=0 直线L1的参数方程可写成X=x1,Y=y1, Z=z1 +t,代入平面方程得: t ) D 0 1 C(z 1 B y 1 A x + + + + = C A x B y C z D 解 得 t 1 + 1 + 1 + = −