
简单多边形三角剖分的算法:考查连续三个 顶点A,B,C,若AC完全在多边形内部,则可输出 △ABC为一个剖分后形成的三角形,删除点B 后再对少了一个顶点的多边形继续进行。 简单多边形的顶点序列为P,P1,P1,那么算 法可描述如下: SIMPLE POLYGON TRIANGULATION 1.(准备)Qo-Po; 2.〔剖分)若n>3,则做2.1~2.2,否则转到步3: 2.1Q1←-点序列中Q的下一个顶点;Q2←-点 序列中Q的下一个顶点; 2.2若Test(Q,Q1,Q2)为真,则做: 输出△QQ1Q2
简单多边形三角剖分的算法:考查连续三个 顶点A,B,C,若AC完全在多边形内部,则可输出 △ABC为一个剖分后形成的三角形,删除点B 后再对少了一个顶点的多边形继续进行。 简单多边形的顶点序列为P0 ,P1 ,Pn-1 ,那么算 法可描述如下: SIMPLE POLYGON TRIANGULATION 1.〔准备〕Q0←P0 ; 2.〔剖分〕若n>3,则做2.1~2.2,否则转到步3: 2.1 Q1←点序列中Q0的下一个顶点;Q2←点 序列中Q1的下一个顶点; 2.2 若Test(Q0 ,Q1 ,Q2 )为真,则做: 输出△Q0Q1Q2 ;

从点序列中删除顶点Q: n←n-1, 返回步2开头; 否则做Q←Q1,返回步2.1; 3.〔最后输出)输出点序列中剩下三点为最后一个三 角形,然后算法结束。 函数Test是对△Qo9,92进行检查,分两步实现, 第一步检查Qo,Q1,Q2是否是一个在Q,的左转,若不然, 是右转,则QQ,在多边形外部而可以回答假而结束。 第二步可对原多边形中除去Qo,Q1,Q2这三点的其它点, 对每一点都考查它对三角形的包含性,若有一点被包 含则就可以回答假而结束,只有其它点都在三角形外 部时才能回答真而结束
从点序列中删除顶点Ql ; n←n-1; 返回步2开头; 否则做Q0←Q1 ,返回步2.1; 3.〔最后输出〕输出点序列中剩下三点为最后一个三 角形,然后算法结束。 函数Test是对△Q0 Q1 Q2进行检查,分两步实现, 第一步检查Q0 ,Q1 ,Q2是否是一个在Ql的左转,若不然, 是右转,则Q0 Q2在多边形外部而可以回答假而结束。 第二步可对原多边形中除去Q0 ,Q1 ,Q2这三点的其它点, 对每一点都考查它对三角形的包含性,若有一点被包 含则就可以回答假而结束,只有其它点都在三角形外 部时才能回答真而结束
最小权三角剖分或最小三角剖分 如果一个三角剖分中选取的对角线的总长 度最小。 任意的凸多边形最小三角剖分 V2 V3 V3 V1 V4 V4 V5 VO V5 V6 V6 (1) (2)
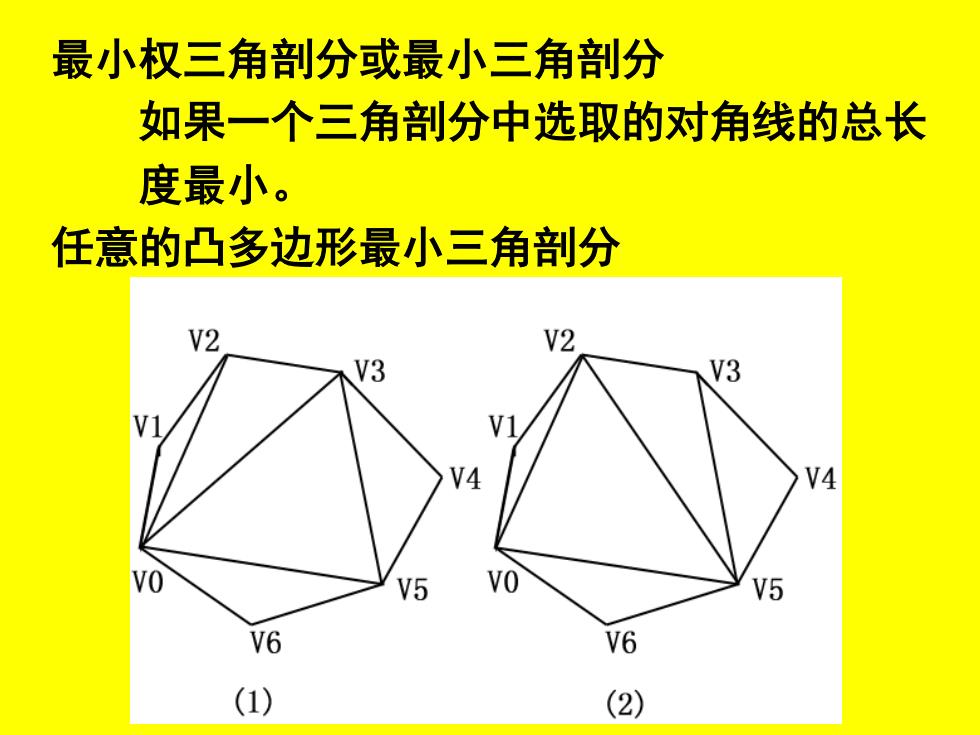
最小权三角剖分或最小三角剖分 如果一个三角剖分中选取的对角线的总长 度最小。 任意的凸多边形最小三角剖分

事实3 在n边形(n≥3)的任意一种三角剖分中 每一对相邻顶点中至少有一个顶点是某条对 角线的端点。 因为若相邻顶点V,V+都不是某条对角线 的端点,则区域(W;-1,V,V+,V+2)中没有对角 线,因而也就没有被三角剖分。 事实4如果VV:是三角剖分的一条对角线,则 一定存在某顶点Vk,使得VVk和VkV是多边形 的边或对角线。 因为若不然,一定存在以VV:为边界的某 个区域没有被三角剖分
事实3 在n边形(n≥3)的任意一种三角剖分中, 每一对相邻顶点中至少有一个顶点是某条对 角线的端点。 因为若相邻顶点Vi ,Vi+1都不是某条对角线 的端点,则区域(Vi-1 ,Vi ,Vi+1,Vi+2)中没有对角 线,因而也就没有被三角剖分。 事实4 如果Vi Vj是三角剖分的一条对角线,则 一定存在某顶点Vk ,使得Vi Vk和Vk Vj是多边形 的边或对角线。 因为若不然,一定存在以Vi Vj为边界的某 个区域没有被三角剖分

顶点序列Vo,V,一,Vn确定的凸n边形的最小 三角剖分 挑选两个相邻顶点比方选V和V1,由事实 3知道在最小三角剖分中,必有另一顶点Vk, 或者使VV是对角线,或者使VoYk是对角线。 对有n个顶点的多边形,V的选取方法 有n-3种。 对于每个可能的Vk用对角线VoVk(或VVk) 把原多边形剖分成两个较小的多边形,这样 原问题就被分成为两个子问题。 往下需要寻找分成的两个较小凸多边形 的最小三角剖分。(递归)
• 顶点序列V0 ,V1 --,Vn-1确定的凸n边形的最小 三角剖分 挑选两个相邻顶点比方选V0和V1 ,由事实 3知道在最小三角剖分中,必有另一顶点Vk , 或者使V1 Vk是对角线,或者使V0 VK是对角线。 对有n个顶点的多边形,Vk的选取方法 有n-3种。 对于每个可能的Vk用对角线V0 Vk (或V1 Vk ) 把原多边形剖分成两个较小的多边形,这样 原问题就被分成为两个子问题。 往下需要寻找分成的两个较小凸多边形 的最小三角剖分。(递归)
选择剖分方法,使得每次剖分后所得的子 问题只涉及一条原多边形的对角线。 由事实4知在最小剖分中的对角线一定与 另外一点构成三角形。 V2 V3 V3 VO (1) (2)
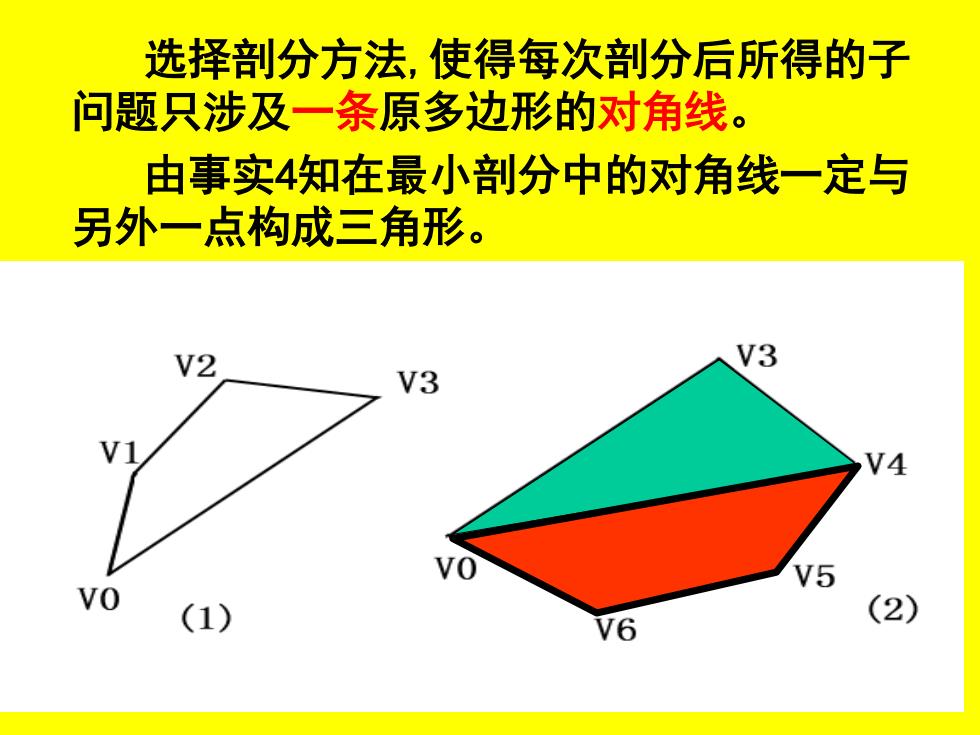
选择剖分方法,使得每次剖分后所得的子 问题只涉及一条原多边形的对角线。 由事实4知在最小剖分中的对角线一定与 另外一点构成三角形

现在一般地说明所要使用的剖分方法。引 人记号Sis,表示一个子多边形y,V+1,,Vs-1 的最小三角剖分问题。子多边形由V开始的$ 个顶点按顺时针向排列围成。 每个子问题$中都农涉及原多边形一条对 角线。为了解S,必须考虑如下三种情况: 字成 这时构成一个三角形 ViViS-2V1 2. 选择顶点V这时构成一个三角形 VV+1Vs-1得到一个学问题S+,S-1 3.对2≤k≤S-3,选择V这时构成一 个三角形yVVs-1,得到两个芋问题S,k+1和 S+k,s-k°
现在一般地说明所要使用的剖分方法。引 人记号Sis,表示一个子多边形Vi ,Vi+1,…,Vi+s-1 的最小三角剖分问题。子多边形由Vi开始的S 个顶点按顺时针向排列围成。 每个子问题Sis中都仅涉及原多边形一条对 角线。为了解Sis,必须考虑如下三种情况: 1. 选择顶点Vi+S-2 ,这时构成一个三角形 Vi Vi+S-2 Vi+S-1 ,得到一个子问题Si,S-1 2. 选择顶点Vi+1,这时构成一个三角形 Vi Vi+1Vi+S-1 ,得到一个子问题Si+1,S-1。 3. 对2≤k≤S-3,选择Vi+k这时构成一 个三角形Vi Vi+kVi+S-1 ,得到两个子问题Si,k+1和 Si+k,S-k
实际上可以把三种情况概括为一句话,即对 1≤k≤S-2,把S:分解成两个子问题S,k1和 Sk$。容易验证k=1和k=S-2时,各自有一个子 问题不成其为问题,但这不影响一般的讨论。 Si,k+1 Vi+k Si+k,S-k Vi+s-1
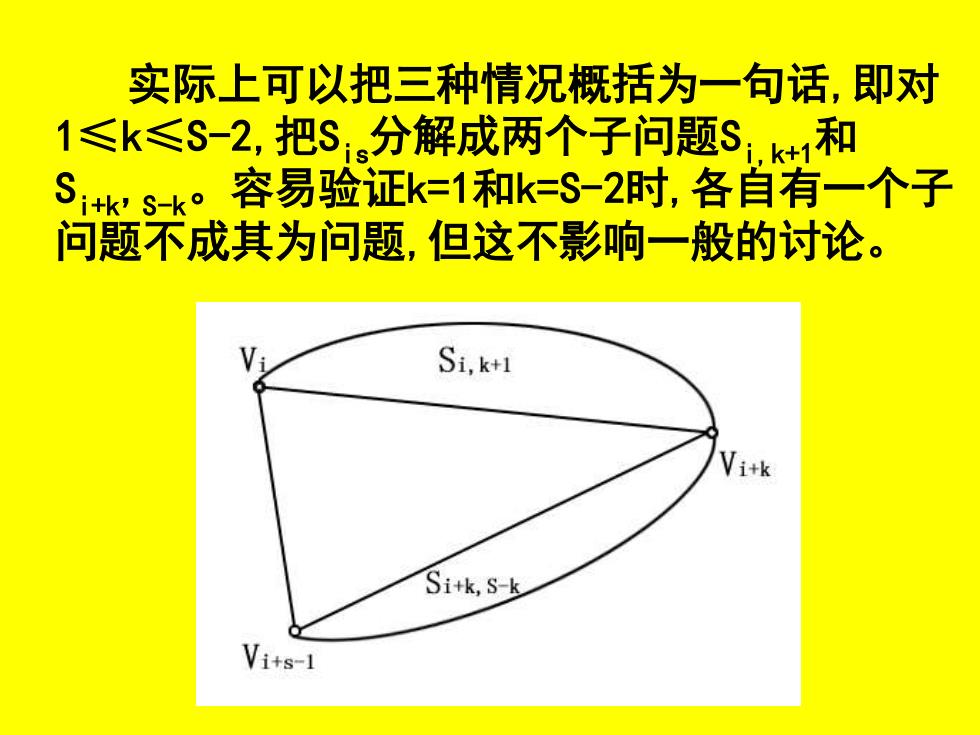
实际上可以把三种情况概括为一句话,即对 1≤k≤S-2,把Sis分解成两个子问题Si,k+1和 Si+k,S-k。容易验证k=1和k=S-2时,各自有一个子 问题不成其为问题,但这不影响一般的讨论

Cs记子问题Ss的解 Cs的公式如下: Cis-min[Cik++CitkS-K+D(ViVi+K)+D(Vi+k Vi+s-1)] 1≤k≤S-2 如果VpVq是对角线,则D(VpVq)是它的长 度;若VpVq是原多边形的边,则D(VpVq)=0;如 果S<4,则Cs0。这因为Cs是最小三角剖分中 引人对角线的总长度,原多边形的边不是对角 线,当$<4时也不必引入对角线
CiS记子问题SiS的解 CiS的公式如下: CiS=min[Ci,k+1+Ci+k,S-k+D(ViVi+k)+D(Vi+kVi+S-1 )] 1≤k≤S-2 如果VpVq是对角线,则D(VpVq)是它的长 度;若VpVq是原多边形的边,则D(VpVq)=0;如 果S<4,则CiS=0。这因为CiS是最小三角剖分中 引人对角线的总长度,原多边形的边不是对角 线,当S<4时也不必引入对角线
对前面说明的凸七边形,要计算的各Cs,有 0≤i≤6,4≤S≤6。可用填表的方式逐个计算。 C07-75. 43 C06-53. C16-55. C26-57. C3664. C46-59. C56-59. C6663. 54 22 58 49 78 78 62 C05=37. C1531. C2535. C3537. C45=45. C5539. C65=38. 54 81 49 74 50 98 09 C04-16. C1416. C24-15. C34=15. C44-22. C54-22. C64-17. 16 16 65 65 69 69 89
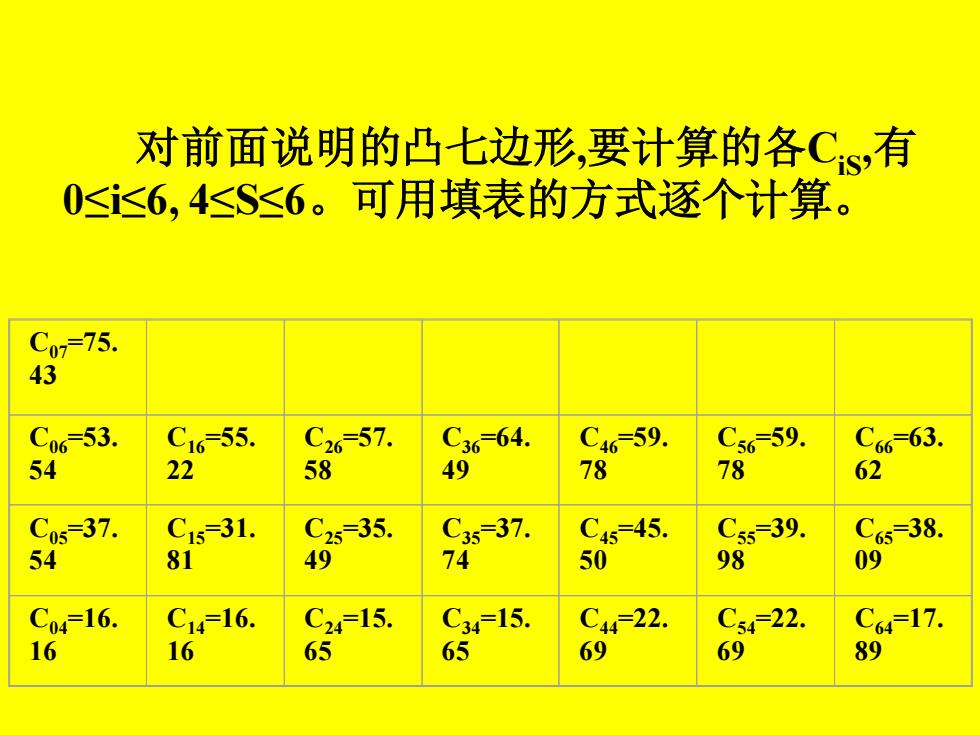
对前面说明的凸七边形,要计算的各CiS,有 0≤i≤6, 4≤S≤6。可用填表的方式逐个计算。 C07=75. 43 C06=53. 54 C16=55. 22 C26=57. 58 C36=64. 49 C46=59. 78 C56=59. 78 C66=63. 62 C05=37. 54 C15=31. 81 C25=35. 49 C35=37. 74 C45=45. 50 C55=39. 98 C65=38. 09 C04=16. 16 C14=16. 16 C24=15. 65 C34=15. 65 C44=22. 69 C54=22. 69 C64=17. 89