
第二章图形基元的显示 •扫描转换将图形描述转换成用象 素矩阵表示的过程 图形基元(输出图形元素) 图形 系统能产生的最基本图形 ·线段、圆、多边形
第二章 图形基元的显示 • 扫描转换 将图形描述转换成用象 素矩阵表示的过程 • 图形基元(输出图形元素)图形 系统能产生的最基本图形 • 线段、圆、多边形

·第一节直线扫描转换算法 ·第二节圆的扫描转换算法 •第三节区域填充
• 第一节 直线扫描转换算法 • 第二节 圆的扫描转换算法 • 第三节 区域填充

第一节直线扫描转换算法 ·DDA直线扫描转换算法 ·Bresenhami画线算法
第一节 直线扫描转换算法 • DDA直线扫描转换算法 • Bresenham画线算法

(22 x1d

设待画线段两端点的坐标值 (x1,y1)和(x2,y2),假定x1<x2 y=mx+b m=(y2-y1)/(x2-x1) b=(x2y1-x1y2)/(x2-x1) m ≤1,对x每增1取允许的各整 数值
设待画线段两端点的坐标值 (x1,y1)和(x2,y2),假定 x1<x2 y=mx+b m=(y2-y1)/(x2-x1) b=(x2y1-x1y2)/(x2-x1) ,对x每增1取允许的各整 数值 m 1

△y_y1一y: m X41一X void DDALine(int x1,int y1,int x2,int y2) double dx,dy,e,x,y; dx=x2-x1; dy-y2-y1; e=(fabs(dx)>fabs(dy))?fabs(dx):fabs(dy); dx/=e; dy/=e;
i 1 i i 1 i x x y y Δ x Δ y m − − = = + + void DDALine(int x1,int y1,int x2,int y2) { double dx,dy,e,x,y; dx=x2-x1; dy=y2-y1; e=(fabs(dx)>fabs(dy))?fabs(dx):fabs(dy); dx/=e; dy/=e;

x=x1; y=yl; for(int i=1;i<=e;i++) SetPixel((int)(x+0.5),(int)(y+0.5)); x+=dx; y+=dy;
x=x1; y=y1; for(int i=1;i<=e;i++) { SetPixel((int)(x+0.5), (int)(y+0.5)); x+=dx; y+=dy; } }
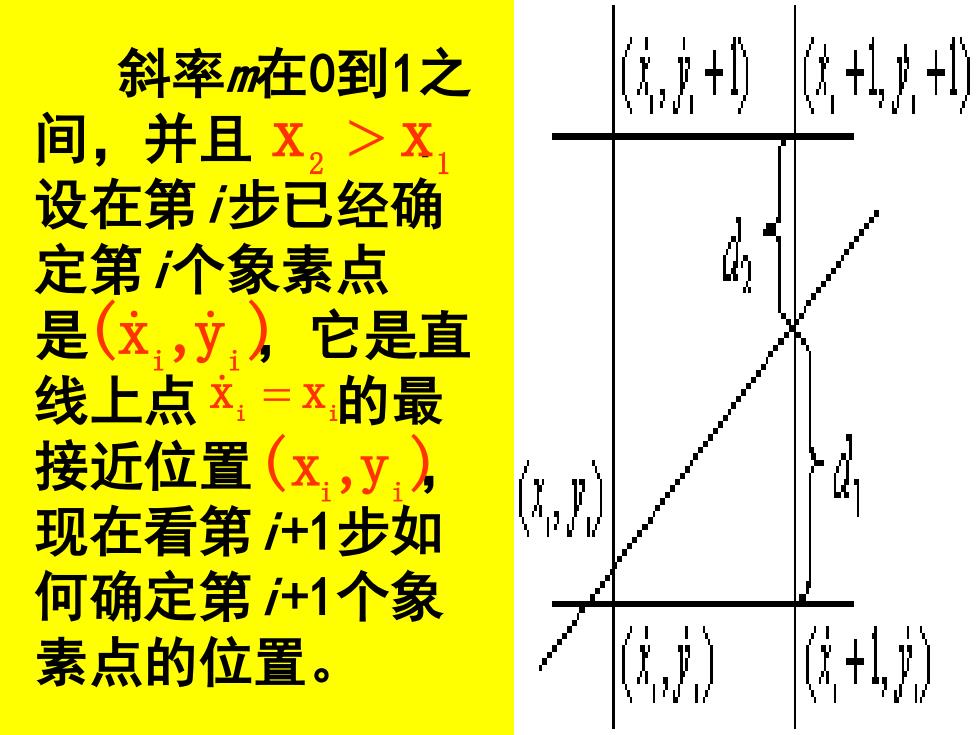
斜率m在0到1之 ,+《 间,并且X,>X 设在第步已经确 定第个象素点 是(文,立,它是直 线上点文=x的最 接近位置(x,y, 现在看第+1步如 何确定第+1个象 素点的位置
斜率m在0到1之 间,并且 . 设在第i步已经确 定第i个象素点 是 ,它是直 线上点 的最 接近位置 , 现在看第i+1步如 何确定第i+1个象 素点的位置。 2 1 x x (x i ,y i ) (xi ,yi ) xi = xi

d=y-立:=m(仪+1)+b-y d2=(位+1)-y=(位+1)-m(这+1)-b d-d2=2m区+1)-2y+2b-1 >d。,下一个象素点取(区+1立+1) d1<d,下-个象素点取(文+1,立,) d=d2, 取两象素点中的任意一个
d d 2m(x 1 ) 2y 2 b 1 1 − 2 = i + − i + − d (y 1 ) y (y 1 ) m (x 1 ) b d y y m (x 1 ) b y 2 i i 1 i i i = + − = + − + − = − = + + − d1 d2 ,下一个象素点取 (x 1 ,y 1 ) i i + + d1 d2 ,下一个象素点取 (x i +1 ,y i ) d1 = d2 ,取两象素点中的任意一个
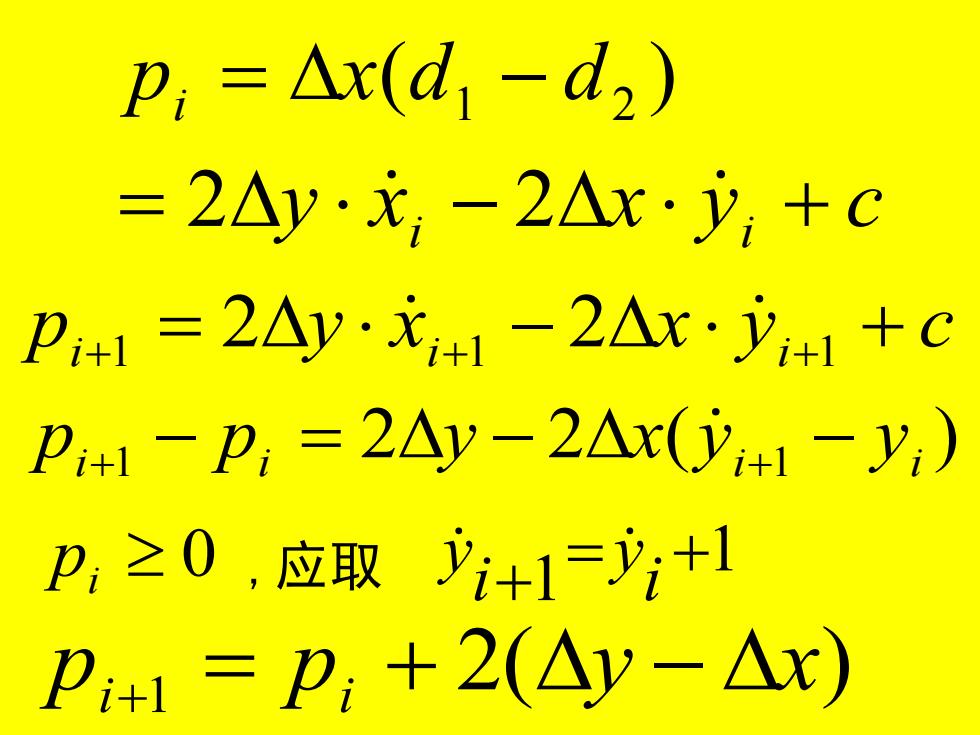
p,=△x(d1-d2) =2△y·x-2△x·y,+C p,+1=2Ay·元+1-2△x·y1+C P+1-p=2Ay-2△x(y+1-y) P,≥0,应取+1=+1 卫+1=P;+2(△y-△x)
p y x x y c i+1 = 2 i+1 − 2 i+1 + y x x y c p x d d i i i = − + = − 2 2 ( ) 1 2 2 2 ( ) i 1 i i 1 i p − p = y − x y − y + + pi 0 ,应取 1 1 = + + i y i y 2( ) 1 p p y x i+ = i + −