
(2)设选出的连续三点是P,P,Pk,则向量 PP与PP的夹角a的绝对值,应大于某 个预先给定的限制阈值ao°,若小于a 则不应选取而应考虑是能将P,至P和 P;至Pk两段合并。 P Pk
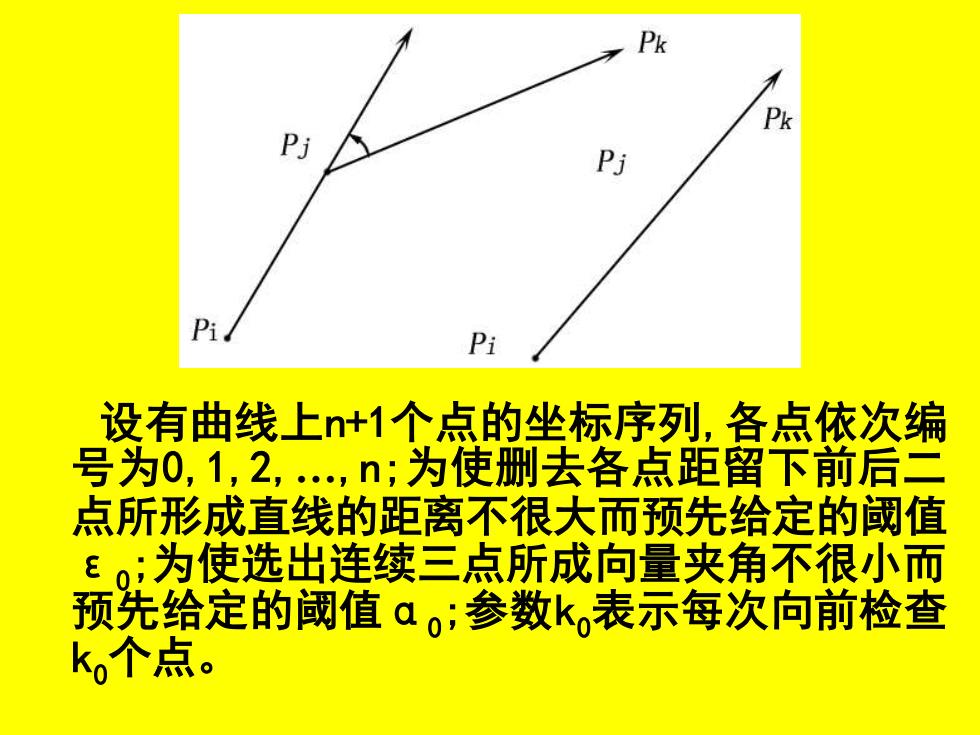
(2)设选出的连续三点是Pi ,Pj ,Pk ,则向量 Pi Pj与Pj Pk的夹角α的绝对值,应大于某 个预先给定的限制阈值α0。,若小于α0 , 则Pj不应选取而应考虑是否能将Pi至Pj和 Pj至Pk两段合并
Pk Pi 设有曲线上+1个点的坐标序列,各点依次编 号为0,1,2,,n;为使删去各点距留下前后二 点所形成直线的距离不很大而预先给定的阈值 ε。:为使选出连续三点所成向量夹角不很小而 预先给定的阈值αo:参数k,表示每次向前检查 k个点
设有曲线上n+1个点的坐标序列,各点依次编 号为0,1,2,…,n;为使删去各点距留下前后二 点所形成直线的距离不很大而预先给定的阈值 ε0 ;为使选出连续三点所成向量夹角不很小而 预先给定的阈值α0 ;参数k0表示每次向前检查 k0个点

1.〔初始化)i←0,j←0,k←ko输出点编号 0,s←1。{i记最近己选之点,初始起点0为必 选,j记待检查之点,算法中保持i≤j,待检查 线是点到k的直线。} 2.〔共线性检查〕检查点到k间各点共线性。 若不能通过,距离直线PP最远的点是m,则 k←m返回本步开头。否则继续。{本步必能通 过,因最坏在k=j+1时能通过。} 3.〔暂定j前后两线方向)L2←点到k的方向, 若i=j则L1←L2,到6;否则继续。L2是暂定找 到从向后的新线方向,L1是前次找到原有线 方向。}
1.〔初始化〕 i←0,j←0,k←k0 ,输出点编号 0,s←1。{i记最近己选之点,初始起点0为必 选,j记待检查之点,算法中保持i≤j,待检查 线是点j到k的直线。} 2.〔共线性检查〕检查点j到k间各点共线性。 若不能通过,距离直线Pj Pk最远的点是m,则 k←m返回本步开头。否则继续。{本步必能通 过,因最坏在k=j+1时能通过。} 3.〔暂定j前后两线方向〕L2←点j到k的方向, 若i=j则L1←L2,到6;否则继续。{L2是暂定找 到从j向后的新线方向,L1是前次找到原有线 方向。}

4.〔向量夹角检查〕检查P,P,Pk三点形成 二向量L1和L2的夹角的绝对值,若可以通 过即应发生合并,做j←i然后返2,否则继 续。{本步检查通过即点j不能选取,而要 检查原i到k的直线。} 5.〔找到一个选取点)i←j,L1←点j到k的 方向,输出点编号j,s←s+1。 6.〔准备下次)j←k,k←k+ko,若k>n则k←n, 若j≤n-1则返2,否则继续。 7.〔最后取点)输出点编号n,算法结束
4.〔向量夹角检查〕检查Pi ,Pj ,Pk三点形成 二向量L1和L2的夹角的绝对值,若可以通 过即应发生合并,做j←i然后返2,否则继 续。{本步检查通过即点j不能选取,而要 检查原i到k的直线。} 5.〔找到一个选取点〕i←j,L1←点j到k的 方向,输出点编号j,s←s+1。 6.〔准备下次〕j←k,k←k+k0 ,若k>n则k←n, 若j≤n-1则返2,否则继续。 7.〔最后取点〕输出点编号n,算法结束
P2 PO P6 i←0,j←0,k←k(3) PPk即P0P3,若通过; j-k,k←k+k0, PPk即P3P6
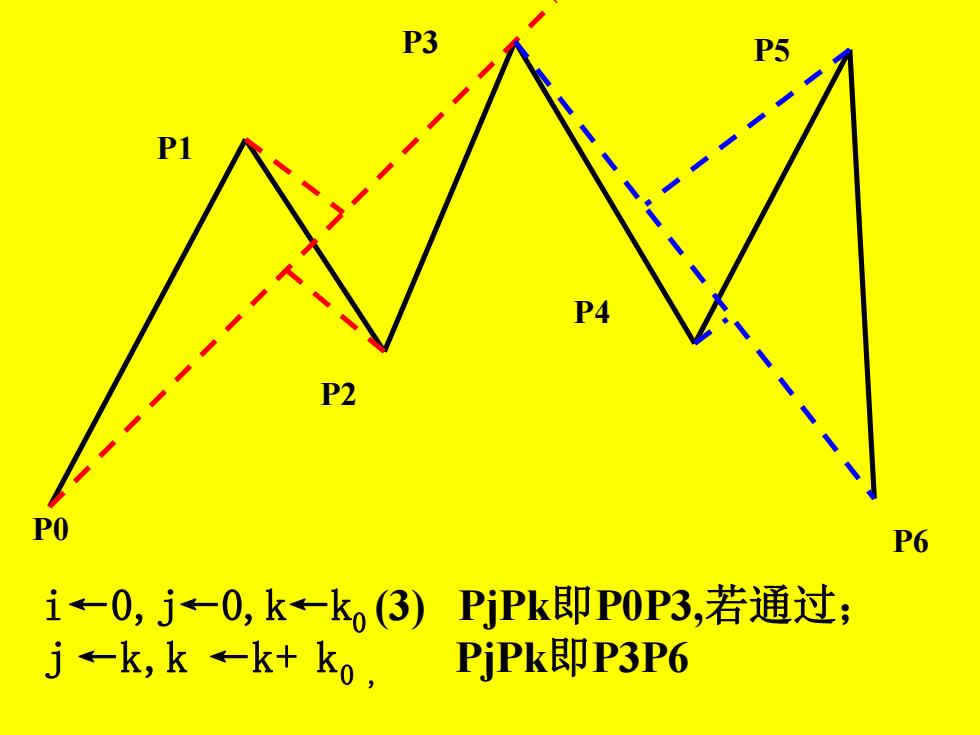
P0 P1 P2 P3 P4 P5 P6 i←0,j←0,k←k0 (3) PjPk即P0P3,若通过; j ←k,k ←k+ k0 , PjPk即P3P6

带树法 带树是一棵二叉树,树的每个结点对 应一个矩形带段,这样每个结点可由八个 字段组成,前六个字段描述矩形带段,后二 个是指向两个子结点的指针,即矩形带段 的起点是(xby),终点是(x。,y。)。相对从 起点到终点的连线,矩形有两边与之平行, 两边与之垂直,平行两边与之距离分别为 W,和Wo
带树法 带树是一棵二叉树,树的每个结点对 应一个矩形带段,这样每个结点可由八个 字段组成,前六个字段描述矩形带段,后二 个是指向两个子结点的指针, 即矩形带段 的起点是(xb ,yb ),终点是(xe ,ye )。相对从 起点到终点的连线,矩形有两边与之平行, 两边与之垂直,平行两边与之距离分别为 wl和wr

X汤 Yb Xe Ye W Wr P1 P2 (Xe,Ye) w Wr (Xb,Yb)

设要表示的曲线是由经过适当选取已确 定的一组离散点Po,P1,,Pn序列给出,则生 成表示曲线的分辨率为W的带树的算法,可简 略描述如下: 1.找出由起点Po,终点P确定的矩形带段,其 中包含P至P的全部点,构造此矩形带段的对 应结点并令为根。 2. 找出P至Pn之间距离连线即Pn为最远的点Pk, 然后对P。至P和P.至P这两组点分别做与步1 中相同的构造矩形带段及对应结点的操作, 产生的两个结点,分别是根的左右子结点。 3. 反复执行上述操作,直到所产生结点的 W=w+w≤Wo。这样的结点是叶结点
设要表示的曲线是由经过适当选取已确 定的一组离散点P0 ,P1 ,…,Pn序列给出,则生 成表示曲线的分辨率为w0的带树的算法,可简 略描述如下: 1. 找出由起点P0 ,终点Pn确定的矩形带段,其 中包含P0至Pn的全部点,构造此矩形带段的对 应结点并令为根。 2. 找出P0至Pn之间距离连线P0 Pn为最远的点Pk , 然后对P0至Pk和Pk至Pn这两组点分别做与步1 中相同的构造矩形带段及对应结点的操作, 产生的两个结点,分别是根的左右子结点。 3. 反复执行上述操作,直到所产生结点的 w=wl +wr ≤w0。这样的结点是叶结点

设表示曲线有5个点 (3,7)(9,12),(15,4),(18,5),(20,7),取分辨 率W,=1,则上述算法构造的带树 (9,12) 12 (20,7) (3,7) (15,4)》 (18,5) 8 12 16 20 3720753 379120 91220704.8 91215400 15420700.6
设表示曲线有5个点 (3,7)(9,12),(15,4),(18,5),(20,7) ,取分辨 率w0 =1,则上述算法构造的带树

以不同的分辨率显示用带树表示的曲线 设给出允许的分辨率为W*,表示曲线 的带树的分辨率为Wo,并设w≤w*,则显 示算法可简略描述如下: 从根结点开始,若当前正考查结点的 W=W,+w.≤w*,则显示该结点对应的矩形 带段;若不然,即W>w*则转去分别考查 该结点的左右两个子结点,对子结点做 同样的处理。左右子结点都被显示的结 点就认为是被显示了,按此看法,显示带 树表示的曲线就是显示带树的结点
以不同的分辨率显示用带树表示的曲线 设给出允许的分辨率为w*,表示曲线 的带树的分辨率为w0 ,并设w0≤w*,则显 示算法可简略描述如下: 从根结点开始,若当前正考查结点的 W=wl +wr ≤w*,则显示该结点对应的矩形 带段;若不然,即W> w*则转去分别考查 该结点的左右两个子结点,对子结点做 同样的处理。左右子结点都被显示的结 点就认为是被显示了,按此看法,显示带 树表示的曲线就是显示带树的结点