
第六节裁剪 裁剪就是去掉窗口外的不可见部分, 保留窗口内的可见部分的过程。 裁剪区域:矩形、任意图形 裁剪对象:点、线段、多边形、 二维或三维形体 假设窗口的两个对角顶点分别 是(%)、(xr),则同时满足下列不等式的 点(x,y)是要保留的点,否则就要被舍弃: 7≤x≤xr,yb≤syt
第六节 裁剪 裁剪就是去掉窗口外的不可见部分, 保留窗口内的可见部分的过程。 裁剪区域:矩形、任意图形 裁剪对象:点、线段、多边形、 二维或三维形体 假设窗口的两个对角顶点分别 是 、 ,则同时满足下列不等式的 点 是要保留的点,否则就要被舍弃: ( , ) b y l x ( , ) t y r x (x, y) t y y b y r x x l x ,

直线段裁剪算法 Cohen-Sutherland:算法 该算法的基本思想是:首先判断直线 段是否全部在窗口内,是,则保留;不 是,则再判断是否完全在窗口之外,如 是,则舍弃。如果这两种情况都不属于 ,则将此直线段分割,对分割后的子线 段再进行如前判断。直至所有直线段和 由直线段分割出来的子线段都已经确定 了是保留还是舍弃为止
直线段裁剪算法 Cohen-Sutherland算法 该算法的基本思想是:首先判断直线 段是否全部在窗口内,是,则保留;不 是,则再判断是否完全在窗口之外,如 是,则舍弃。如果这两种情况都不属于 ,则将此直线段分割,对分割后的子线 段再进行如前判断。直至所有直线段和 由直线段分割出来的子线段都已经确定 了是保留还是舍弃为止

1001 1000 1010 yt 0001 0000 0010 yo 0101 0100 0110 x Xr 图3.25 区域编码 编码:如果该区域在窗口的上方,则代码的第一位为1 如果该区域在窗口的下方,则代码的第二位为1;如果 该区域在窗口的右侧,则代码的第三位为1;如果该区 域在窗口的左侧,则代码的第四位为1
编码:如果该区域在窗口的上方,则代码的第一位为1; 如果该区域在窗口的下方,则代码的第二位为1;如果 该区域在窗口的右侧,则代码的第三位为1;如果该区 域在窗口的左侧,则代码的第四位为1

D H 算法步骤如下: 4 第一步:编码 J 第二步:判别 B 第三步:求交 第四步:对剩下的 线段重复以上各步 XL 图3.26 Cohen-sutherland裁剪箅
算法步骤如下: 第一步:编码 第二步:判别 第三步:求交 第四步:对剩下的 线段重复以上各步

算法的程序实现如下 函数Cohen Suther I and,用来实现算法 函数makecode)用来编码,利用数值位运算 double xI,xr,yt,yb;(事先给出窗口的 位置,四个数值是已知的) void Cohen Sutherland(double x0,y0,x2,y2) { int c,cl,c2; double x,y; makecode(x0,y0,c1);makecode(x2,y2,c2); while(c1!=0‖c2!=0) if (c1&c2!=0)return;
算法的程序实现如下 函数Cohen_Sutherland用来实现算法 函数makecode用来编码,利用数值位运算 double xl, xr, yt, yb; (事先给出窗口的 位置,四个数值是已知的) void Cohen_Sutherland(double x0, y0, x2, y2) { int c, c1, c2; double x, y; makecode(x0, y0,c1); makecode(x2, y2, c2); while (c1!=0 || c2!=0) { if (c1&c2!=0) return;

c=c1;if (c==0)c=c2; if(c&1==1){y=y0+(y2-y0)*(x1-x0)/(x2-x0);x=x1;} else if(c&2==2){y=y0+(y2-y0)*(xr-x0)/(x2-x0); x=xr; else if(c&4==4){x=x0+(x2-x0)*(yb-y0)/y2-y0); y=yb; else if(c&8==8){x=x0+(x2-x0)*(yt-y0)/(y2-y0); y=yt; if (c==c1) {x0=x;y0=y;makecode(x,y,c1);} else {x2=x;y2=y;makecode(x,y,c2);} showline(x0,y0,x2,y2);∥显示可见线段
c=c1; if (c==0) c=c2; if (c&1==1){y=y0+(y2-y0)*(x1-x0)/(x2-x0); x=x1;} else if (c&2==2){y=y0+(y2-y0)*(xr-x0)/(x2-x0); x=xr;} else if (c&4==4){x=x0+(x2-x0)*(yb-y0)/(y2-y0); y=yb;} else if (c&8==8){x=x0+(x2-x0)*(yt-y0)/(y2-y0); y=yt;} if (c==c1) {x0=x; y0=y; makecode(x, y, c1);} else {x2=x; y2=y; makecode(x, y, c2);} } showline(x0, y0, x2, y2); //显示可见线段}
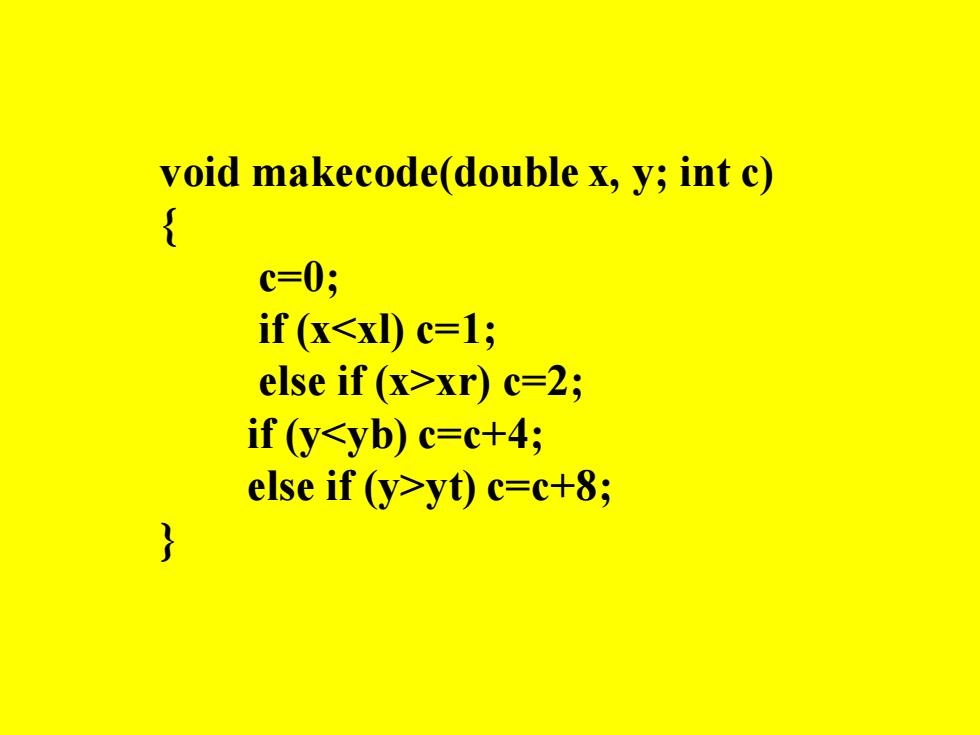
void makecode(double x,y;int c) c=0; if (xxr)c=2; if (yyt)c=c+8;
void makecode(double x, y; int c) { c=0; if (xxr) c=2; if (yyt) c=c+8; }

中点分割算法 设要裁剪的直线段为0。中点分割算法 的基本思想如下:可分成两个过程平行进行, 即从0点出发找出离点0最近的可见点,和从 P点出发找出离点P最近的可见点。这两个 最近可见点的连线就是原直线段的可见部分。 从出发找最近可见点的方法是先求的0中 中点。重复上过程,直到长度小于给定的小数 为止
设要裁剪的直线段为 。中点分割算法 的基本思想如下:可分成两个过程平行进行, 即从 点出发找出离点 最近的可见点,和从 点出发找出离点 最近的可见点。这两个 最近可见点的连线就是原直线段的可见部分。 从 出发找最近可见点的方法是先求的 中 点 ,若 不能定为显然不可见,则取 代替,否则取 代替,再对新的求 中点。重复上过程,直到长度小于给定的小数 为止。 P1 0 P m P m P P0 1 P m P 0 1 P P 0 P P1 0 P 0 1 P P m P P0 中点分割算法

Po A 卫 B 图3.27 中点分割薛法

P是否可见? P=P exit PP显然不可见? 原线完全不可见 香 exit P.=(p6+p)/2 pa-pl<8? Po=Px exit PP显然不可见? 是 Po=P P=P 图3.28中点分割算法框图