
第六章 树
第六章 树
6.1 树的基本概念和术语 6.1.1 树的定义 [例] 3 5 6 8 10 11 ·树的特点:①有一个总根。 ②没有分枝相交。 ③树有层次
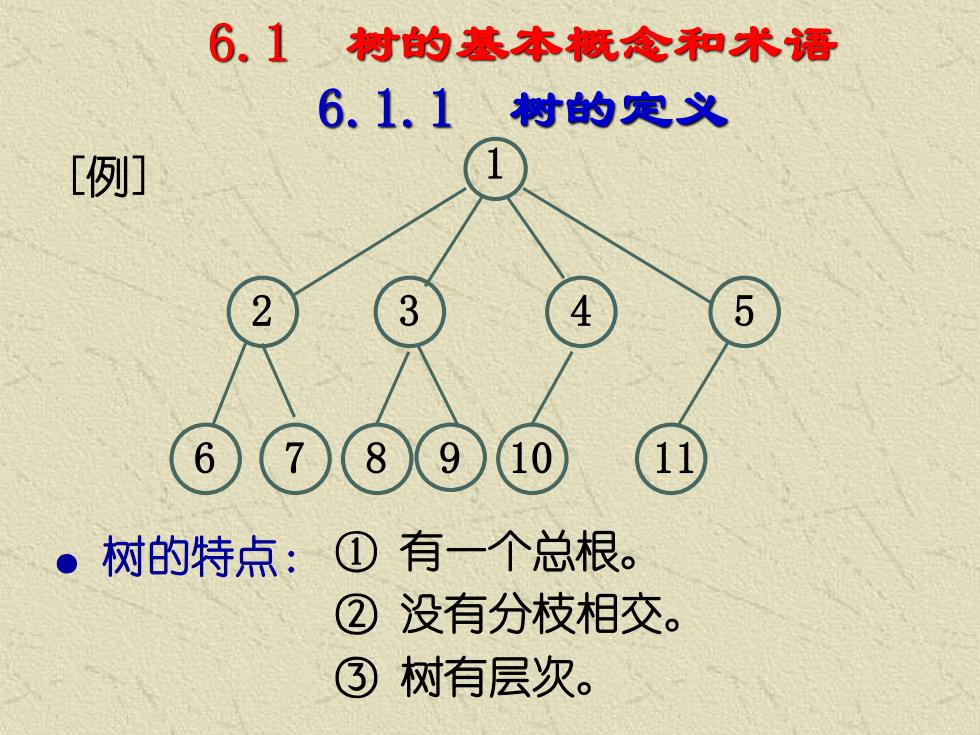
6.1 树的基本概念和术语 6.1.1 树的定义 [例] 1 8 5 6 3 4 7 2 9 10 11 ● 树的特点: ① 有一个总根。 ② 没有分枝相交。 ③ 树有层次

。树的定义: 树是N>=0个结点组成的有限集合T, 该有限集合具有如下特性: ①除N=0的树外,有且仅有一个特定的称 为根的结点· ②其余结点分为m(m>=0)个互不相交的 有限集合T1,T2, ..,Tm,其中 每一个集合都是一棵树·
● 树的定义: 树是 N >= 0 个结点组成的有限集合 T, 该有限集合具有如下特性 : ① 除 N = 0 的树外 , 有且仅有一个特定的称 为根的结点 . ② 其余结点分为 m( m >= 0 ) 个互不相交的 有限集合 T1, T2 , … ,Tm , 其中 每一个集合都是一棵树

。基本术语: ①度 :一个结点的度是该结点所具有子 树的数目。 ②叶结点:度为零的结点,也就是没有子树 的结点(终端结点)。 ③树的度:一棵树内所有结点的度的最大数 称为树的度。 ④子女和双亲:子女指树的子树的根结点; 双亲即该结点
● 基本术语: ① 度 :一个结点的度是该结点所具有子 树的数目。 ② 叶结点 :度为零的结点,也就是没有子树 的结点(终端结点)。 ③ 树的度 :一棵树内所有结点的度的最大数 称为树的度。 ④ 子女和双亲 :子女指树的子树的根结点 ; 双亲即该结点

⑤层:根结点到某个结点的路径长度称为结点 的层数。 根结点在第0层;若结点X在L 层上则其孩子在(L+1)层。 ⑥树的深度:树中结点的最大层称为树的深 度。 ⑦兄弟和堂兄弟:同一个双亲孩子之间称为兄 弟;其双亲在同一层的结 点互为堂兄弟
⑤ 层 :根结点到某个结点的路径长度称为结点 的层数。 根结点在第 0 层; 若结点 X 在 L 层上则其孩子在(L+1)层。 ⑥ 树的深度 :树中结点的最大层次称为树的深 度。 ⑦ 兄弟和堂兄弟 : 同一个双亲孩子之间称为兄 弟 ; 其双亲在同一层的结 点互为堂兄弟

⑧祖先:从根到该结点所经分支上的所有结点。 ⑨子孙:某结点为根的子树中的任一结点都称 为该结点子孙。 ⑩森林:是m(m≥0)棵互不相交的树的集合
⑧ 祖先:从根到该结点所经分支上的所有结点。 ⑨ 子孙:某结点为根的子树中的任一结点都称 为该结点子孙。 ⑩ 森林:是m (m≧0)棵互不相交的树的集合

6.1二叉树 6.2.1 二又树的定义和主要性质 1定义 ●二叉树的特征 ① 二叉树每个结点的度不大于2; ② 二叉树的子树有左右之分。 ·定义:二叉树是结点的有限集合,它必须满足 下面的一个条件: (1)它是空集。 (2)它由一个根结点的左右子树构成,且其 左右子树满足二叉树定义
6.1 二叉树 6.2.1 二叉树的定义和主要性质 1 定义 ● 二叉树的特征 ① 二叉树每个结点的度不大于2; ② 二叉树的子树有左右之分。 ● 定义:二叉树是结点的有限集合,它必须满足 下面的一个条件: (1)它是空集。 (2)它由一个根结点的左右子树构成,且其 左右子树满足二叉树定义
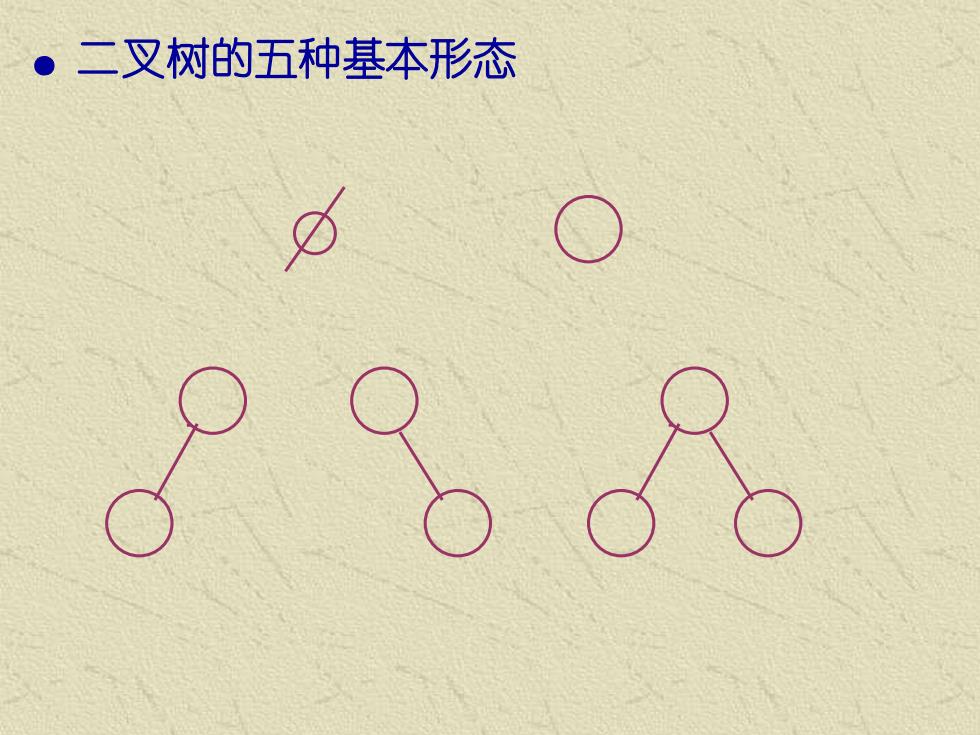
。二叉树的五种基本形态
● 二叉树的五种基本形态

2二叉树的性质 。性质1:二叉树中层数为i的结点至多有2个, i≥0
2 二叉树的性质 ● 性质1:二叉树中层数为i的结点至多有2 i个, i≧0

2二叉树的性质 ●性质2:高度为k的二叉树中至多有2+1-1(k ≥0)个结点
2 二叉树的性质 ● 性质2:高度为k的二叉树中至多有2 k+1-1(k ≧ 0)个结点