
第五节投影 投影就是把n维空间中的点投射到小于 n维的空间中去。 投影是如下形成的:首先在三维空问中 确定一个投影中心和一个投影平面,然后 从投影中心引出一些投射直线,这些直线 通过形体上的每一点,与投影平面相交, 在投影平面上就形成了形体的投影。根据 投影中心与投影平面之间距离的不同,投 影可以分为平行投影和透视投影
第五节 投影 投影就是把n维空间中的点投射到小于 n维的空间中去。 投影是如下形成的:首先在三维空间中 确定一个投影中心和一个投影平面,然后 从投影中心引出一些投射直线,这些直线 通过形体上的每一点,与投影平面相交, 在投影平面上就形成了形体的投影。根据 投影中心与投影平面之间距离的不同,投 影可以分为平行投影和透视投影

平行投影当投影中心与投影平面 的距离为无穷远时,投射直线成为 一 组平行线. 透视投影 当投影中心与投影平 面的距离是有限数值时,投射直线 交于一点,形成灭点. 平行投影正交投影和斜交投影 正交投影 投影方向与投影平面 的法向相同.常见的正交投影是正 视投影、顶视投影和侧视投影
平行投影 当投影中心与投影平面 的距离为无穷远时,投射直线成为 一组平行线. 透视投影 当投影中心与投影平 面的距离是有限数值时,投射直线 交于一点,形成灭点. 平行投影 正交投影和斜交投影 正交投影 投影方向与投影平面 的法向相同. 常见的正交投影是正 视投影、顶视投影和侧视投影

如果投影平面Z=0,投影方向是沿Z轴, 设三维空间中有普通坐标为(x,y,z的一 点P,投影后,成为点P”,普通坐标 为(x',y,z),可知: x'=x,y'=y,z'=0 [yz=ky名
如果投影平面Z=0,投影方向是沿Z轴, 设三维空间中有普通坐标为 的一 点 P,投影后,成为点P’,普通坐标 为 ,可知: = 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 x' y' z' 1 x y z 1 (x, y,z) (x' , y' ,z') x' = x, y' = y, z' = 0
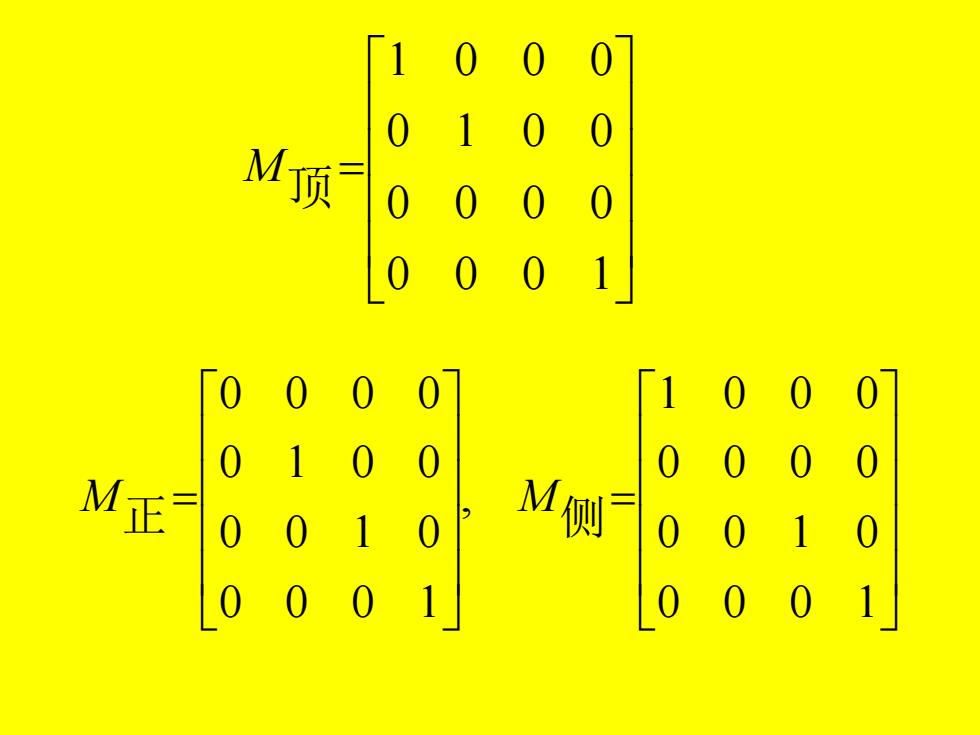
M顶 0 M正 M侧
= 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 M 顶 = = 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 , 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 M 正 M 侧
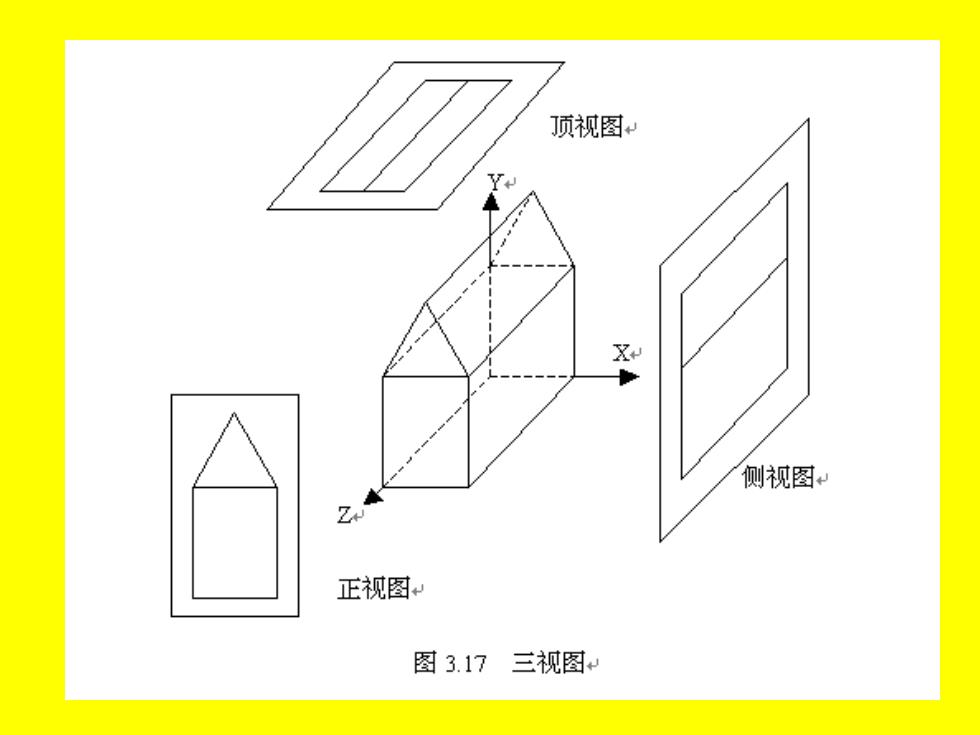
顶视图 X 侧视图 正视图+ 图3.17三视图

投影平面垂直于坐 标轴的正交投影称为 正投影。正交投影还 有另一种常见的情形 是等轴投影,这种投 影要求投影平面的法 线方向,即投影方向 与三个坐标轴的夹角 图3.18单位正方体的等轴投影图 都相等。这种投影能 使在三个坐标轴方向 上有相等的透视缩短
投影平面垂直于坐 标轴的正交投影称为 正投影。正交投影还 有另一种常见的情形 是等轴投影,这种投 影要求投影平面的法 线方向,即投影方向 与三个坐标轴的夹角 都相等。这种投影能 使在三个坐标轴方向 上有相等的透视缩短
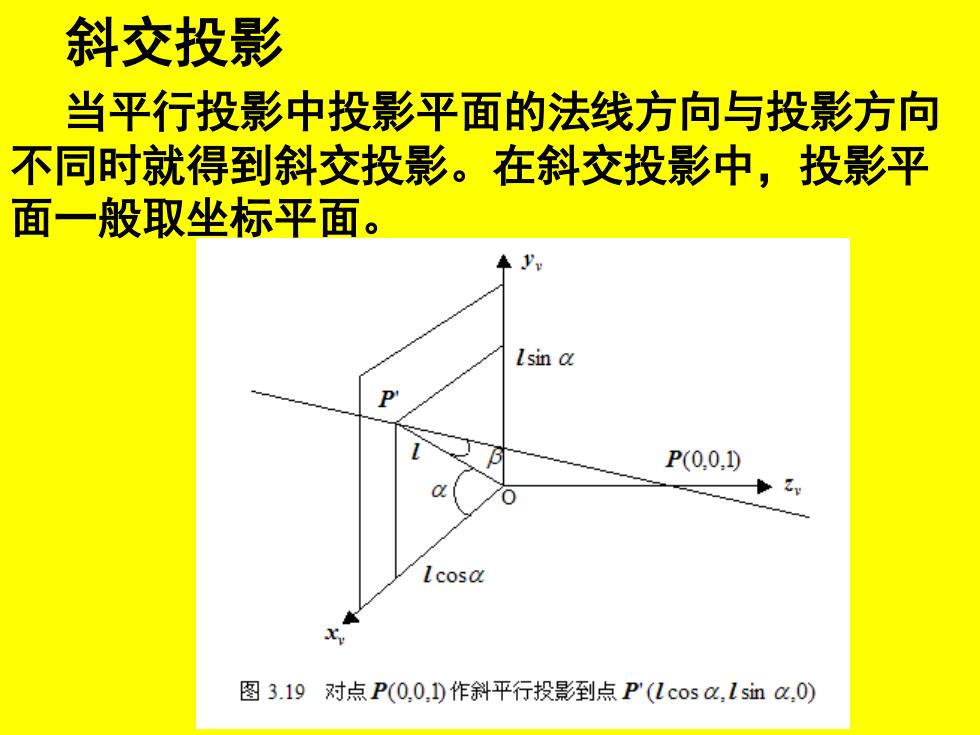
斜交投影 当平行投影中投影平面的法线方向与投影方向 不同时就得到斜交投影。在斜交投影中,投影平 面一般取坐标平面。 Isin a P(0.0.0 0 lcosa 图3.19对点P(0,0.)作斜平行投影到点P(1cosa,Isin a,0)
斜交投影 当平行投影中投影平面的法线方向与投影方向 不同时就得到斜交投影。在斜交投影中,投影平 面一般取坐标平面

设三维空间中有普通坐标为的任意一 点(x,y,z),经斜交投影后所得投影点普通坐 标为(x,y,。显然z=0,有: x'-x Icosa y'-y Isina Z Z x'=x+z●(l●CoS) y'=y+z●(l●sin)
设三维空间中有普通坐标为的任意一 点 ,经斜交投影后所得投影点普通坐 标为 。显然 ,有: (x, y,z) (x' , y' ,z') z' = 0 1 ' sin , 1 ' cos l z l y y z x x = − = − ' ( sin ) ' ( cos ) = + • • = + • • y y z l x x z l
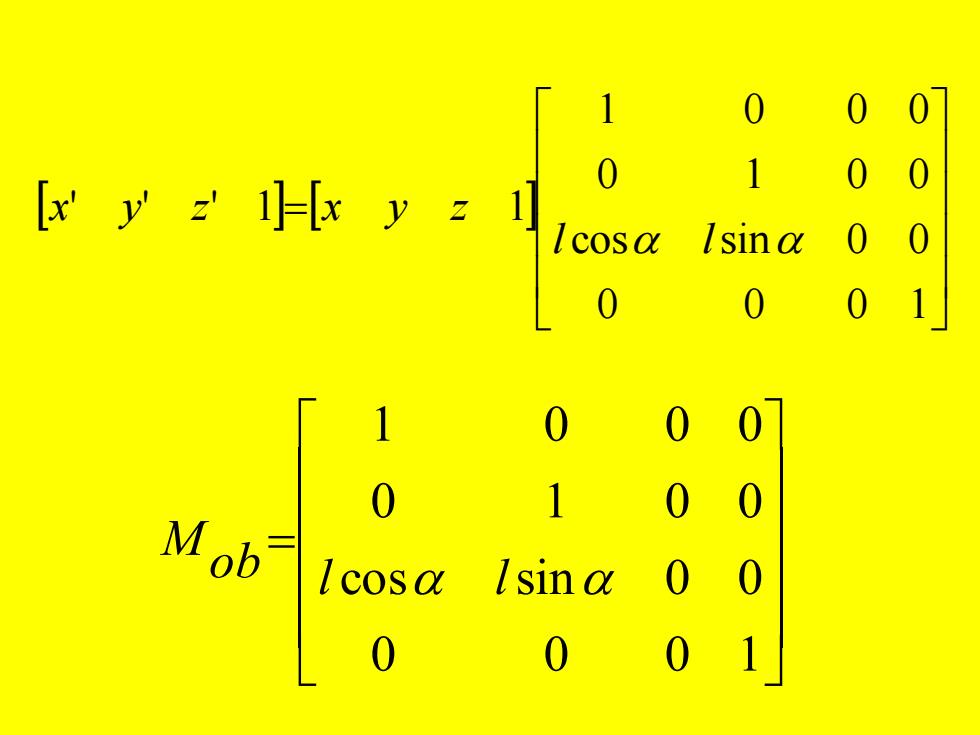
0 0 0 0 1 0 Mob
= 0 0 0 1 cos sin 0 0 0 1 0 0 1 0 0 0 ' ' ' 1 1 l l x y z x y z = 0 0 0 1 cos sin 0 0 0 1 0 0 1 0 0 0 ob l l M

斜交投影中两个比较重要的情形是斜二 测投影和斜等轴投影。斜二测投影使垂直于 投影平面的线段长度缩短为原来的一半;斜等 轴投影使垂直于投影平面的线段仍保持长度. X 图3.20 边长为的正方体的两种斜二测投影的示意图
斜交投影中两个比较重要的情形是斜二 测投影和斜等轴投影。斜二测投影使垂直于 投影平面的线段长度缩短为原来的一半;斜等 轴投影使垂直于投影平面的线段仍保持长度