
void bez to points(int n,int npoints,double Pl,double points)∥P为控制点坐标points为采用几 何作图算法生成的Bezier曲线上的离散点序列 离散点序列points的个数为npoints 控制点P的个数为n+1 double t,delt; delt=l.0/(double)npoints;:/W将参数t npoints等分 t=0.0; for(int i=0;i<=npoints;i++) points[i=decas(n,P,t);∥分别求出 npoints+-1个离散点points的坐标 t+=delt;
void bez_to_points(int n,int npoints,double P[],double points[]) // P为控制点坐标 points为采用几 何作图算法生成的Bezier曲线上的离散点序列 离散点序列points的个数为npoints 控制点P的个数为n +1 { double t,delt; delt=1.0/(double)npoints;//将参数t npoints等分 t=0.0; for(int i=0;i<=npoints;i++) { points[i]=decas(n, P, t); // 分别求出 npoints+1个离散点points的坐标 t+=delt; } }

double decas(int n,double P[l,double t) int m,i; double *R,*Q,P0; R=new double n+1]; Q=new double[n +1]; for(i=0;i0;m--)
double decas(int n,double P[],double t) { int m,i; double *R, *Q, P0; R = new double[n +1]; Q = new double[n +1]; for(i=0;i0;m--) {

/n次Bezier曲线在点t的值,可由两条n-1次 Bezier曲线在点t的值通过线性组合而求得。 for(i=0;i<=m-1;++) Q=R+t*(R+1-R); for(i=0;i<=m-1;i++) R[]=Q [i]; P0=R0]; delete R; delete Q; return (PO);
//n次Bezier曲线在点t的值,可由两条n-1次 Bezier曲线 在点t的值通过线性组合而求得。 for(i=0;i<= m -1;i++) Q[i]= R [i]+t*( R [i+1]- R [i]); for(i=0;i<= m -1;i++) R[i]= Q [i]; } P0=R[0]; delete R; delete Q; return (P0); }
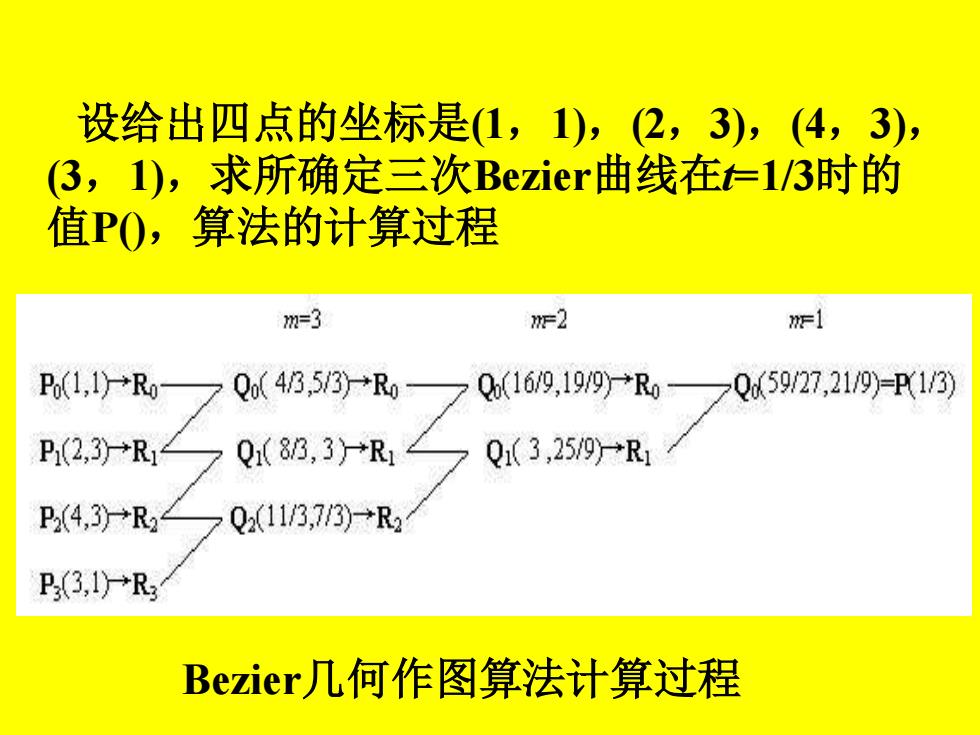
设给出四点的坐标是1,1),(2,3),(4,3) (3,1),求所确定三次Bezier曲线在t=1/3时的 值P0,算法的计算过程 m=3 mF2 mF1 P1,1尸→R0 Q(43,53)-R Q(169,19/9y→R0 Qd59/27,21/9)=P1/3) P1(2,3)-R1 Q1(83,3尸R Q1(3,259-R P2(4,3)+R2 Q2(11/3,7/3)→R2 P(3,1→R Bezier几何作图算法计算过程
设给出四点的坐标是(1,1),(2,3),(4,3), (3,1),求所确定三次Bezier曲线在t=1/3时的 值P(),算法的计算过程 Bezier几何作图算法计算过程

设控制点序列Po,P1,,P确定 的n次Bezierl曲线是P(t),用如下递 归方式计算另一组点集: k=0,i=0,1,n 1. k=1,2;…,n,i=kk+1,,n 如果令P,(s)和Pb(s)分别是以控 制点序列8,和哈,唱确 定的Bezierl曲线,其中0≤s≤1,那 么就有:
设控制点序列P0,P1,…,Pn确定 的n次Bezier曲线是P(t),用如下递 归方式计算另一组点集: = = + − − + − = = = ) , k 1,2, ,n , i k ,k 1 , ,n k 1 i 1 P k 1 i ( P 2 1 , k 0 , i 0,1, ,n i P k i P 如果令Pa (s)和Pb (s)分别是以控 制点序列 和 确 定的Bezier曲线,其中0≤s≤1,那 么就有: n n , ,P 1 ,P 0 0 P 1 0 n , ,P n 1 n ,P n n P −
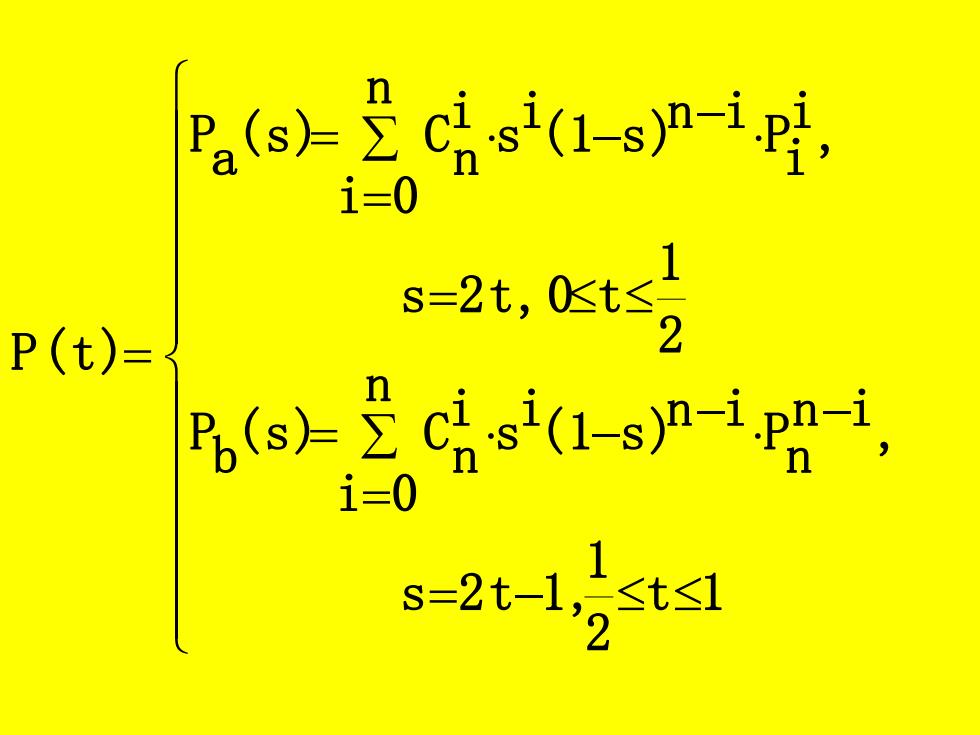
Pa(g>是cs(1-s-ip4, i=0 P(t)= s-2t,0etg Fp(s)c(1-si 1=0 s-2t-1 stal
= − = − − = − = = − = − = t 1 2 1 s 2 t 1 , , n i 0 n i n P n i ( 1 s ) i s i n (s) C b P 2 1 s 2t,0 t , n i 0 i i P n i ( 1 s ) i s i n (s) C a P P(t)

己知四点Po;P1,P23P3, 确定了一 条三次Bezierl曲线P(t),可写出下式, P(e)Bo,3e)8+B1,3e9+2,3e)2+3,3)B B0.32t)8+1,32t)月+2,32t)+,32t)写 0≤t≤ 0.32t-1)+81,32t-1)号+2,32t-1)g+,32t-1) 2Sts1
己知四点P0,P1,P2,P3,确定了一 条三次Bezier曲线P(t),可写出下式, − + − + − + − + + + = = + + + t 1 2 1 , 0 3 (2t 1)P 3,3 B 1 3 (2t 1)P 2,3 B 2 3 (2t 1)P 1,3 B 3 3 (2t 1)P 0,3 B 2 1 0 t , 3 3 (2t)P 3,3 B 2 2 (2t)P 2,3 B 1 1 (2t)P 1,3 B 0 0 (2t)P 0,3 B 3 (t)P 3,3 B 2 (t)P 2,3 B 1 (t)P 1,3 B 0 (t)P 0,3 P(t) B
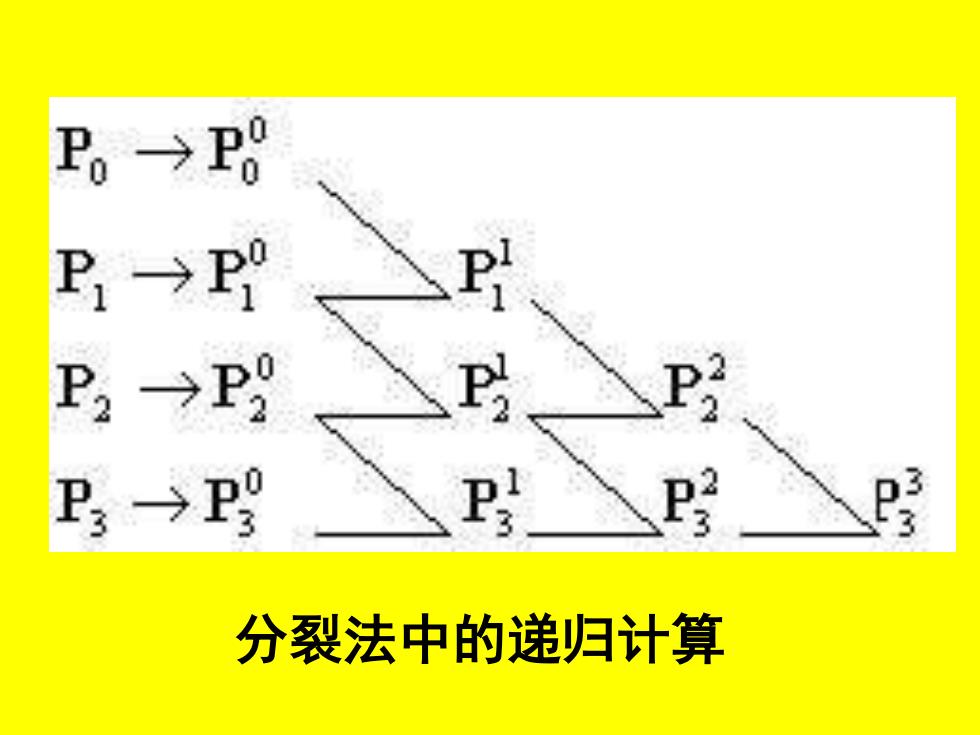
P→P8 P→ P2→P P3→9 分裂法中的递归计算
分裂法中的递归计算
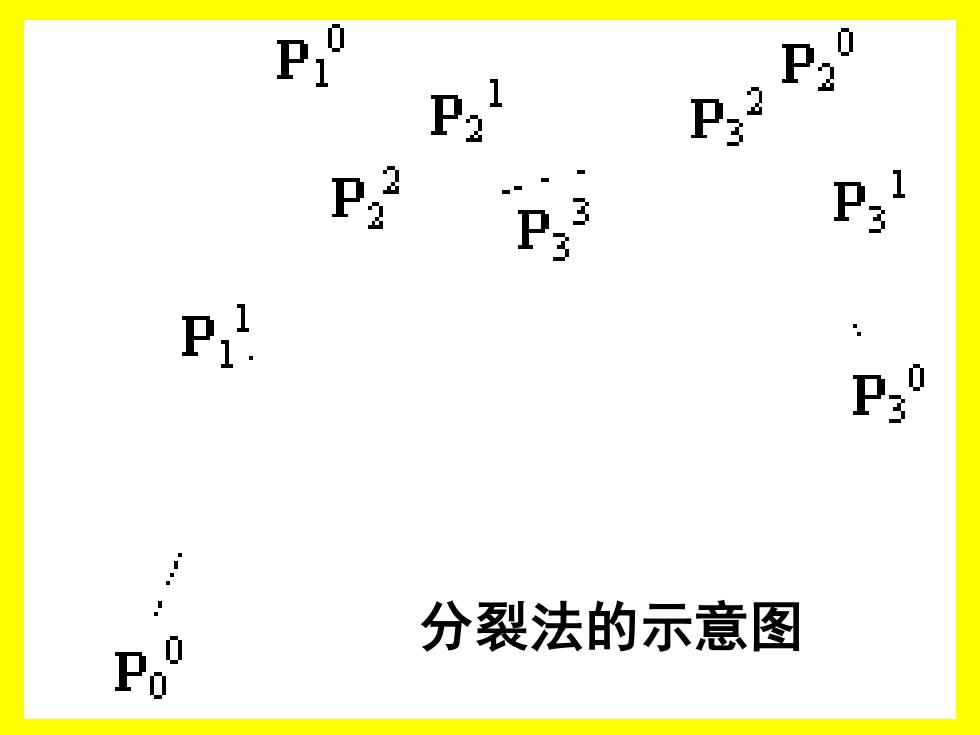
P,2 P 分裂法的示意图
分裂法的示意图

可通过计算验证Bezier曲线由前 后两段构成。现以P的系数为例, 验证两端它的系数是相等的。 左端显然就是B.30)=(1-)3 先看右端。若0≤t≤§,这时就用 前半段的表达式,观察分裂计算图 注意到P中有1份Po,P中有2份, P中是份,P中是日份,因此 全部P的系数是:
可通过计算验证Bezier曲线由前 后两段构成。现以P0的系数为例, 验证两端它的系数是相等的。 左端显然就是 。 先看右端。若0≤t≤ ,这时就用 前半段的表达式,观察分裂计算图 注意到 中有1份P0, 中有 份, 中是 份, 中是 份,因此 全部P0的系数是: 3 ( ) (1 ) 0,3 B t = −t 2 0 1 P0 1 P1 2 1 2 P2 4 1 3 P3 8 1