
Jarvis.算法 1.〔准备〕V←点集S中按x,y字典次序最小的点; d←竖直向下的一个方向向量; 点v送入收集凸壳顶点的队列Q中; S,←S-{vol; u+vo 2.〔一步行进)v,←Wrapp ing(u,d,S); 3.〔准备下次)若v丰vo,则做:V接入队Q后部; S1=S-{u,v}; d←从u到V,的一个方向向量;
Jarvis算法 1.〔准备〕v0←点集S中按x,y字典次序最小的点; d←竖直向下的一个方向向量; 点v0送入收集凸壳顶点的队列Q中; S1←S-{ v0 }; u←v0 2.〔一步行进〕v1←Wrapping(u,d,S1 ); 3.〔准备下次〕若v1≠v0 ,则做: v1接入队Q后部; S1 =S-{u,v1 }; d←从u到v1的一个方向向量;

返步2。 4.〔结束)壳顶点已经全部存入队Q中,算法结束. 其中第2步引入函数Wrapp ing来实现一步行 进。此函数的工作是,对$中所有各点,相对自u 发出方向为d的射线,计算所成倾角。在所有倾角 中取最小,若有多个则选与u距离最远的那个,它 对应的点为函数的返回值。因此在步2求得的v, 是一个行进步找到的下个壳顶点。 Jarvis若点集S中只有较少数点在壳上,则 算法效率很高。若点集$中绝大多数点都在壳上, 算法的效率一般来说就不如Gr aham扫描了
u←v1 返步2。 4.〔结束〕壳顶点已经全部存入队Q中,算法结束. 其中第2步引入函数Wrapping来实现一步行 进。此函数的工作是,对S1中所有各点,相对自u 发出方向为d的射线,计算所成倾角。在所有倾角 中取最小,若有多个则选与u距离最远的那个,它 对应的点为函数的返回值。因此在步2求得的v1 是一个行进步找到的下个壳顶点。 Jarvis 若点集S中只有较少数点在壳上,则 算法效率很高。若点集S中绝大多数点都在壳上, 算法的效率一般来说就不如Graham扫描了

第四节 包含与重叠 ·简单多边形的包含算法 平面上的简单多边形是不相邻的边不能 相交的多边形,设它用顶点坐标的逆时针序 列(0,y0),(x1,y1),,(xn-1,yn-1)确 定,即沿顶点序列前行时内部在左侧。 对平面上坐标为(xp,yp)的任意一点P,包 含性检验问题是判断它是否在所给出简单多 边形的内部
第四节 包含与重叠 • 简单多边形的包含算法 平面上的简单多边形是不相邻的边不能 相交的多边形,设它用顶点坐标的逆时针序 列(x0,y0),(x1,y1),…,(xn-1, yn-1)确 定,即沿顶点序列前行时内部在左侧。 对平面上坐标为(xp,yp)的任意一点P,包 含性检验问题是判断它是否在所给出简单多 边形的内部
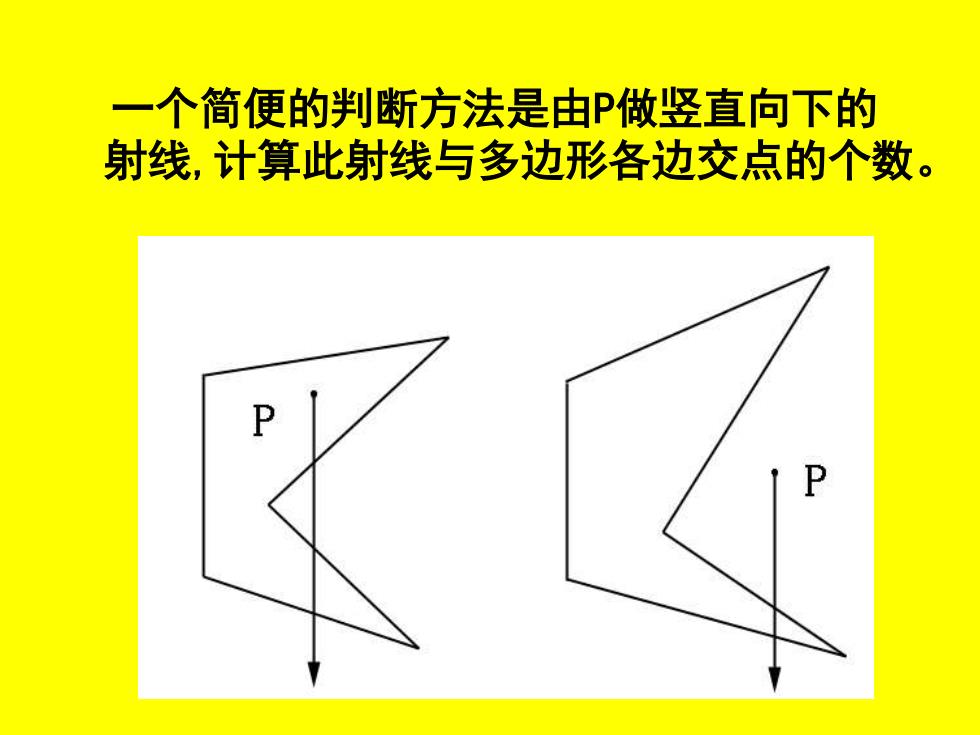
一个简便的判断方法是由P做竖直向下的 射线,计算此射线与多边形各边交点的个数
一个简便的判断方法是由P做竖直向下的 射线,计算此射线与多边形各边交点的个数
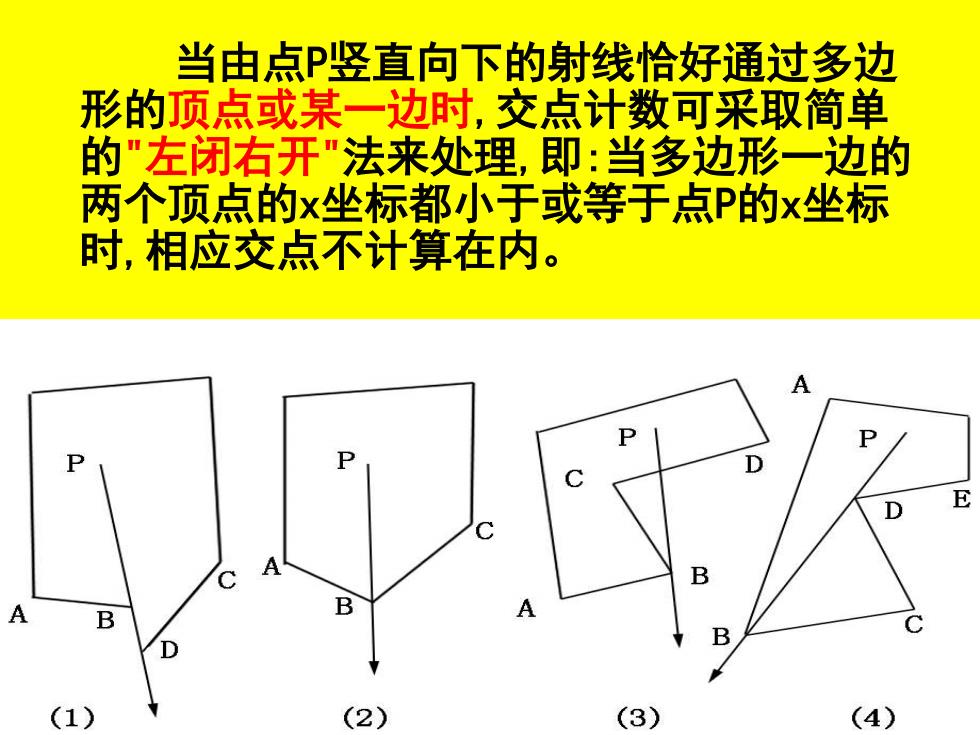
当由点P竖直向下的射线恰好通过多边 形的顶点或某一边时,交点计数可采取简单 的"左闭右开"法来处理,即:当多边形一边的 两个顶点的x坐标都小于或等于点P的x坐标 时,相应交点不计算在内。 P E A B A (1) (2) (3) (4)
当由点P竖直向下的射线恰好通过多边 形的顶点或某一边时,交点计数可采取简单 的"左闭右开"法来处理,即:当多边形一边的 两个顶点的x坐标都小于或等于点P的x坐标 时,相应交点不计算在内

简单多边形包含性检验的算法 1.〔准备)xn←0,yn←y0,m仁-1,i←0; 2.〔排除必不相交情形〕若下列条件有一个成立,则 到4。 2.1p<x;并且p<x+1 2.2Xp≥x;并且p≥x+1; 2.3yp<y:并且yp<y1+1 3.〔计算交点〕yy:+(xp-x)(y+1yi)/(x+1x),分 二种情形: (1)若y=yp,则点P在多边形边界上,算法结束; (2)若y<yp",则m←(-1)m; 4.〔结束判断)i←i+1,若i<n",则返回到2,否则算法 结束,此时若m=-1则点P在多边形外部,m=1则在内部
简单多边形包含性检验的算法 1.〔准备〕xn←x0,yn←y0,m←-1,i←0; 2.〔排除必不相交情形〕若下列条件有一个成立,则 到4。 2.1 xp<xi并且xp<xi+1: 2.2 xp≥xi并且xp≥xi+1; 2.3 yp<yi并且yp<yi+1; 3.〔计算交点〕y=yi +(xp-xi )(yi+1-yi)/(xi+1-xi ),分 二种情形: (1)若y=yp,则点P在多边形边界上,算法结束; (2)若y<yp",则m←(-1)•m; 4.〔结束判断〕i←i+1,若i<n",则返回到2,否则算法 结束,此时若m=-1则点P在多边形外部,m=1则在内部
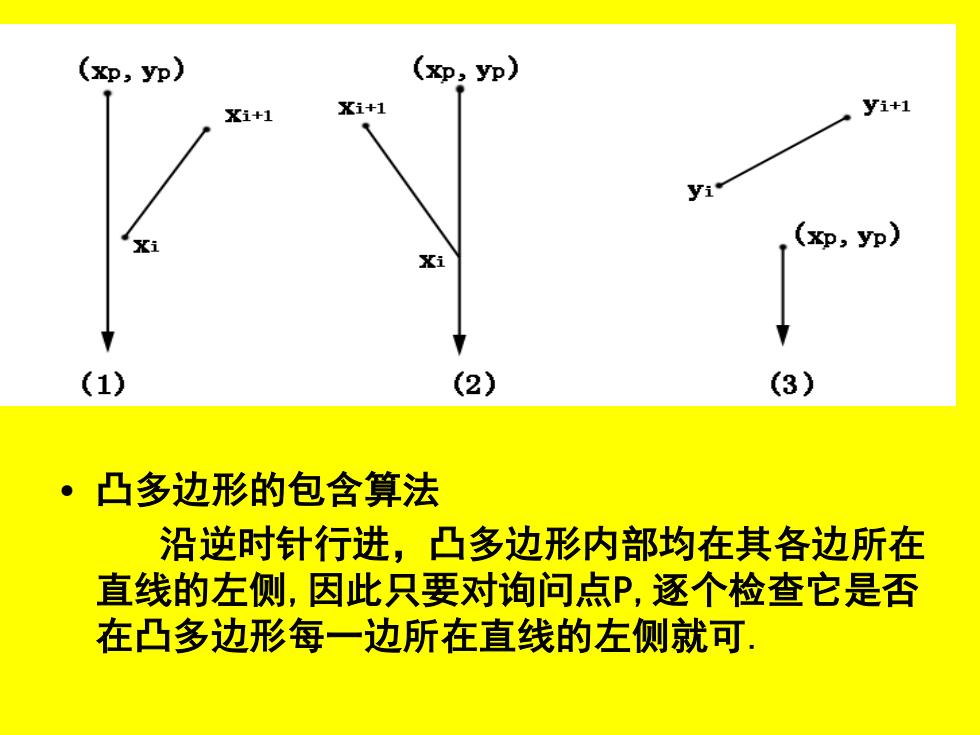
(xp,yp) (xp,yp) X1+1 Xi+1 yi+1 (xp,yp) Xi (1) (2) (3) ·凸多边形的包含算法 沿逆时针行进,凸多边形内部均在其各边所在 直线的左侧,因此只要对询问点P,逐个检查它是否 在凸多边形每一边所在直线的左侧就可
• 凸多边形的包含算法 沿逆时针行进,凸多边形内部均在其各边所在 直线的左侧,因此只要对询问点P,逐个检查它是否 在凸多边形每一边所在直线的左侧就可

判断坐标为xp,yp)的点P是在直线的位置 设直线的端点为(x1,y1)和(x2,y2),直 线方向是由(x1,y1)到(x2,y2)的方向。 直线的方程记为Ax+By+C=0,则有: A=y2-y1,B=x1-x2,C=x2y1-x1y2 计算D: D=Axp+Byp+C 若D0,则点在直线右侧; 若D=0,则点在直线上
判断坐标为(xp,yp)的点P是在直线的位置 设直线的端点为(x1,y1)和(x2,y2),直 线方向是由(x1,y1)到(x2,y2)的方向。 直线的方程记为Ax+By+C=0,则有: A=y2-y1,B=x1-x2,C=x2y1-x1y2 计算D: D=Axp+Byp+C 若D0,则点在直线右侧; 若D=0,则点在直线上
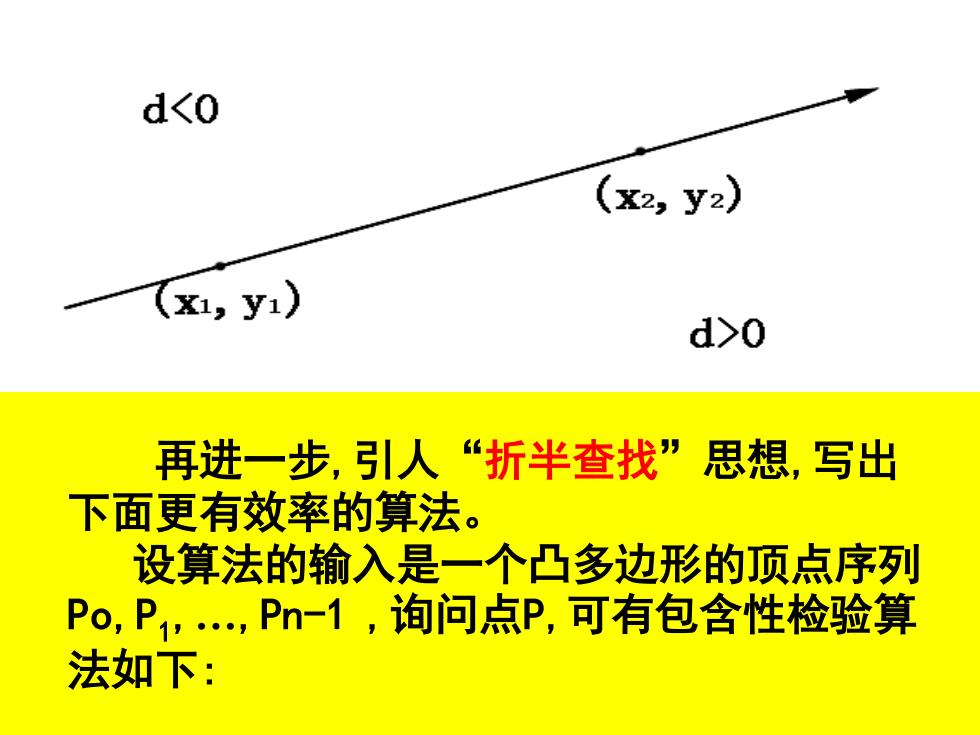
d0 再进一步,引人“折半查找”思想,写出 下面更有效率的算法。 设算法的输入是一个凸多边形的顶点序列 Po,P1,,Pn-1,询问点P,可有包含性检验算 法如下:
再进一步,引人“折半查找”思想,写出 下面更有效率的算法。 设算法的输入是一个凸多边形的顶点序列 Po,P1 ,…,Pn-1 ,询问点P,可有包含性检验算 法如下:

1.〔准备)i←1,j←n-1; 2.〔查找是否结束〕若j-i=1则到4,否则继续; 3.〔折半查找〕k←[(i+)/2],检查询问点相对 直线PoPk的位置关系,分三种情况: 3.1在直线上,若点在线段PoPk上或内部, 则点在原凸多边形内部,若点在线段PoPk延 长线上,则在原凸多边形外;输出回答后算法 结束; 3.2在左侧,i←k返回步2 3.3在右侧,j←k返回步2 4.〔最后检查)检查询问点P对△PPP的包含 性,若在内则也在原凸多边形内部,若在外则 也在原凸多边形外部,输出回答后算法结束
1.〔准备〕i←1,j←n-1; 2.〔查找是否结束〕若j-i=1则到4,否则继续; 3.〔折半查找〕k←[(i+j)/2],检查询问点相对 直线PoPk的位置关系,分三种情况: 3.1 在直线上,若点在线段PoPk上或内部, 则点在原凸多边形内部,,若点在线段PoPk延 长线上,则在原凸多边形外;输出回答后算法 结束; 3.2 在左侧,i←k返回步2 3.3 在右侧,j←k返回步2 4.〔最后检查〕检查询问点P对△P0 Pi Pj的包含 性,若在内则也在原凸多边形内部,若在外则 也在原凸多边形外部,输出回答后算法结束